Файл: Решение Энергия, излучаемая за 1 сек с единицы поверхности абсолютно черного тела, определяется формулой СтефанаБольцмана.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.03.2024
Просмотров: 33
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант №2
1. Черное тело имеет температуру Т1 = 500 К. Какова будет температура Т2 тела, если в результате нагревания поток излучения увеличится в n = 5 раз?
| Дано: Т1 = 500 К 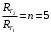 | Решение: Энергия, излучаемая за 1 сек с единицы поверхности абсолютно черного тела, определяется формулой Стефана-Больцмана: 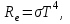 где Re ― излучательная способность абсолютно черного тела; Т ― термодинамическая температура; σ = 5,67∙10−8 Вт/(м2∙К4) ― постоянная Стефана-Больцмана. Поэтому 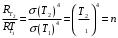 Откуда искомая температура 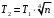 Подставляем числа 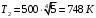 Ответ: 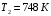 |
| Найти: Т2— ? |
2. На поверхность калия падает свет с длиной волны λ=150 нм. Определить максимальную кинетическую энергию Tmax фотоэлектронов.
| Дано: Калий λ=150 нм А = 2,22 эВ | Решение: Формула Эйнштейна для фотоэффекта: 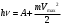 , ,где А – работа выхода Найдем максимальную кинетическую энергию фотоэлектронов, вырываемых из этого металла светом с длиной волны λ=150 нм. Частота этой длины волны равна 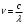 Тогда 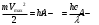 Подставляем числовые значения 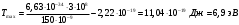 Ответ: 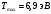 |
| Найти: Tmax— ? |
3. Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол ϑ=π/2? Энергия фотона до рассеяния ε1 = 0,51 МэВ.
| Дано: εф = 0,51 МэВ ϑ=π/2 | Решение: 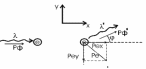 Энергия фотона до рассеяния 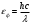 , ,где h – постоянная Планка, с – скорость света, - длина волны фотона По определению импульс фотона и его длина волны связаны соотношением: 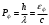 , где h – постоянная Планка, - длина волны фотона , где h – постоянная Планка, - длина волны фотонаСогласно формуле Комптона длина волны после рассеяния равна 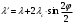 , где с = 2,4310-12 м - Комптоновская длина волны электрона, - угол рассеяния. , где с = 2,4310-12 м - Комптоновская длина волны электрона, - угол рассеяния.Импульс фотона после рассеяния 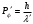 Поэтому 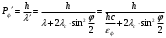 Из закона сохранения импульса имеем: 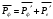 Проектируем вектора на оси Х и Y: На ось Х: 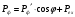 На ось Y: 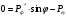 Из первого уравнения 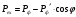 , а из второго , а из второго 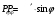 Общий искомый импульс отдачи электрона равен 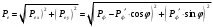 |
| Найти: Еk/ εф— ? |
Упрощаем:
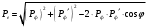
Импульс
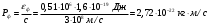
Импульс
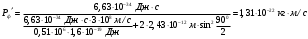
Тогда
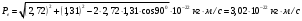
Тогда энергия электрона отдачи равна
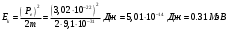
Искомое соотношение равно:
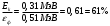
Ответ:
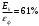
4. Давление р света с длиной волны λ=400 нм, падающего нормально на черную поверхность, равно 2 нПа. Определить число N фотонов, падающих за время t=10 с на площадь S=1 мм2 этой поверхности.
| Дано:_Атом_Н_Решение'>Дано:_Калийλ=400_нм_р_=_2_нПаt=10_сS=1_мм_2_ρ_=_0_Решение'>Дано: Калий λ=400 нм р = 2 нПа t=10 с S=1 мм2 ρ = 0 | Решение: Давление света: 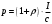 , ,где I – энергия падающая на единицу поверхности за единицу времени, откуда 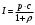 Число фотонов, падающих за t = 10 с на S = 1 мм2 поверхности равно: 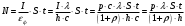 Подставляем числовые значения 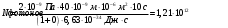 Ответ: 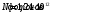 |
| Найти: N— ? |
5. Вычислить по теории Бора радиус r2 второй стационарной орбиты и скорость v2 электрона на этой орбите для атома водорода
| Дано: Атом Н | Решение: Радиус боровской орбиты атома водорода: 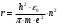 , поэтому , поэтому 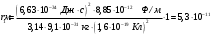 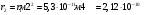 Скорость электрона, находящегося на n-ой орбите 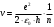 , поэтому , поэтому 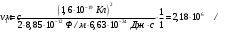 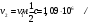 Ответ: 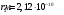 , , 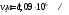 |
| Найти: r2 — ? v2 — ? |
6. Какой кинетической энергией должен обладать электрон, чтобы дебройлевская длина волны была равны его комптоновской длине волны
| Дано:__l_=_0,01_пм_=_10_-14_мm_p_=_1,6710_-27_кг_Решение'>Дано: с = 3108 м/с m = 9,110-31 кг | Решение: Длина волны де Бройля 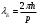 (1) (1) где p – импульс электрона. Будем считать, что мы имеем дело с релятивистским электроном, тогда его импульс связан с кинетической энергией следующим соотношением: 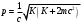 (2) (2)m - здесь и далее масса покоя электрона. Подставим (2) в выражение (1), тогда получим для дебройлевской длины волны соотношение: 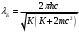 (3) (3)Комптоновская длина волны электрона: 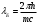 (4) (4)По условию задачи Б С , поэтому мы можем записать: 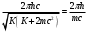 Упростив это выражение и возведя обе части в квадрат, получим квадратное уравнение относительно K: K2 +2mc2K -m2c4 = 0 Решая это уравнение, получим корни: 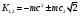 Отрицательный корень не имеет физического смысла, поэтому в качестве результата возьмем положительный корень: 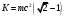 Подставляя числовые значения, получим: 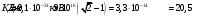 Ответ: 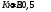 |
| Найти: K — ? |
7. Вычислить минимальную неопределенность координаты покоящегося протона
| Дано: с = 3108 м/с m = 1,6710-27 кг | Решение: Принцип неопределённости Гейзенберга: 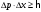 где h – 1,05 · 10-34 Дж·с – постоянная Дирака Тогда неопределенность координаты 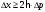 Неопределенность в определении импульса не должна превышать значение самого импульса. Для минимальной оценки импульса электрона 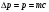 где с – скорость света, с = 3 · 108 м/с Подставим полученные выражения 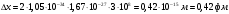 Ответ: 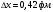 |
| Найти: Δх — ? |
8. Протон находится в бесконечно глубокой одномерной потенциальной яме шириной 0,01 пм. Вычислить в мегаэлектронвольтах энергию основного состояния протона.
| Дано: l= 0,01 пм = 10-14 м mp = 1,6710-27 кг | Решение: Энергия фотона с длиной волны : 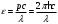 где h = 6,63 · 10-34 Дж·с – постоянная Планка с = 3 · 108 м/с – скорость распространения света в вакууме 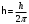 Собственные значения энергии частицы, находящейся в одномерном, бесконечно глубоком, прямоугольном ящике ширинойl, равны: 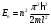 где n 1, 2, 3, … – главные квантовые число (энергетический уровень). m – масса частицы При переходе протона с третьего на второй энергетический уровень его энергия равна 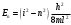 Подставим полученные выражения 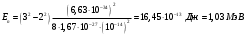 Ответ: 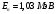 |
| Найти: — ? |
9. Германиевый кристалл, ширина ΔЕ запрещенной зоны в котором равна 0,72 эВ, нагревают от температуры t
1=0°С до температуры t2=15°С. Во сколько раз возрастет его удельная проводимость?
| Дано: ΔЕ = 0,72 эВ t1 = 0°С t2 = 15°С | Решение: Удельная проводимость собственных полупроводников: 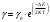 Имеем 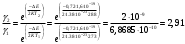 Ответ: 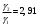 |
| Найти: 1/ 2 — ? |
10. Вычислить дефект массы, энергию связи и удельную энергию связи ядра
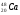
| Дано: 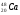 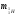 = 1,00783 а.е.м. = 1,00783 а.е.м.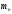 = 1,00867 а.е.м = 1,00867 а.е.м 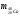 = 47,95253 а.е.м = 47,95253 а.е.м Z =20, A = 48 | Решение: Дефект массы ядра элемента определяется по формуле: 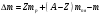 (1) (1)Формулу (1) можно также записать в виде 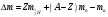 (2) (2)Где ma – масса атома, дефект массы яра которого определяется Подставим в 92) числовые данные, получим 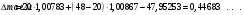 Энергия связи ядра Есв определяется по формуле 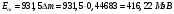 Удельная энергия связи ядра εсв определяется по формуле 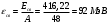 Ответ: 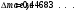 , , 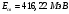 , , 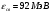 |
| Найти: Δm — ? Есв - ? εсв - ? |

