Дослідження руху механічної системи із застосуванням

теореми про зміну кінетичної енергії

Умова задачі

Механізм, що складається із однорідних стержнів та повзунів з’єднаних шарнірами, розташований у горизонтальній площині. У початковому положенні механізм перебував у стані спокою. Під час руху механізму на його ланки діють момент M та дві сили Q і F. Довжини стержнів: O₁A = 0,5 м; AB = 1,0 м; решту довжин у відповідності до схеми вибрати самостійно. Точка K знаходиться посередині стержня AB. Маси стержнів: m_O1A = 2 кг; m_AB = 4 кг; маса повзуна m_B = 1,5 кг. Для положення механізму, що визначається кутами α, β, γ, δ, φ знайти значення 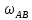. Дослідити залежність кінетичної енергії механізму та шуканого параметру від кута повороту стержня O₁A α є [0 - 2π].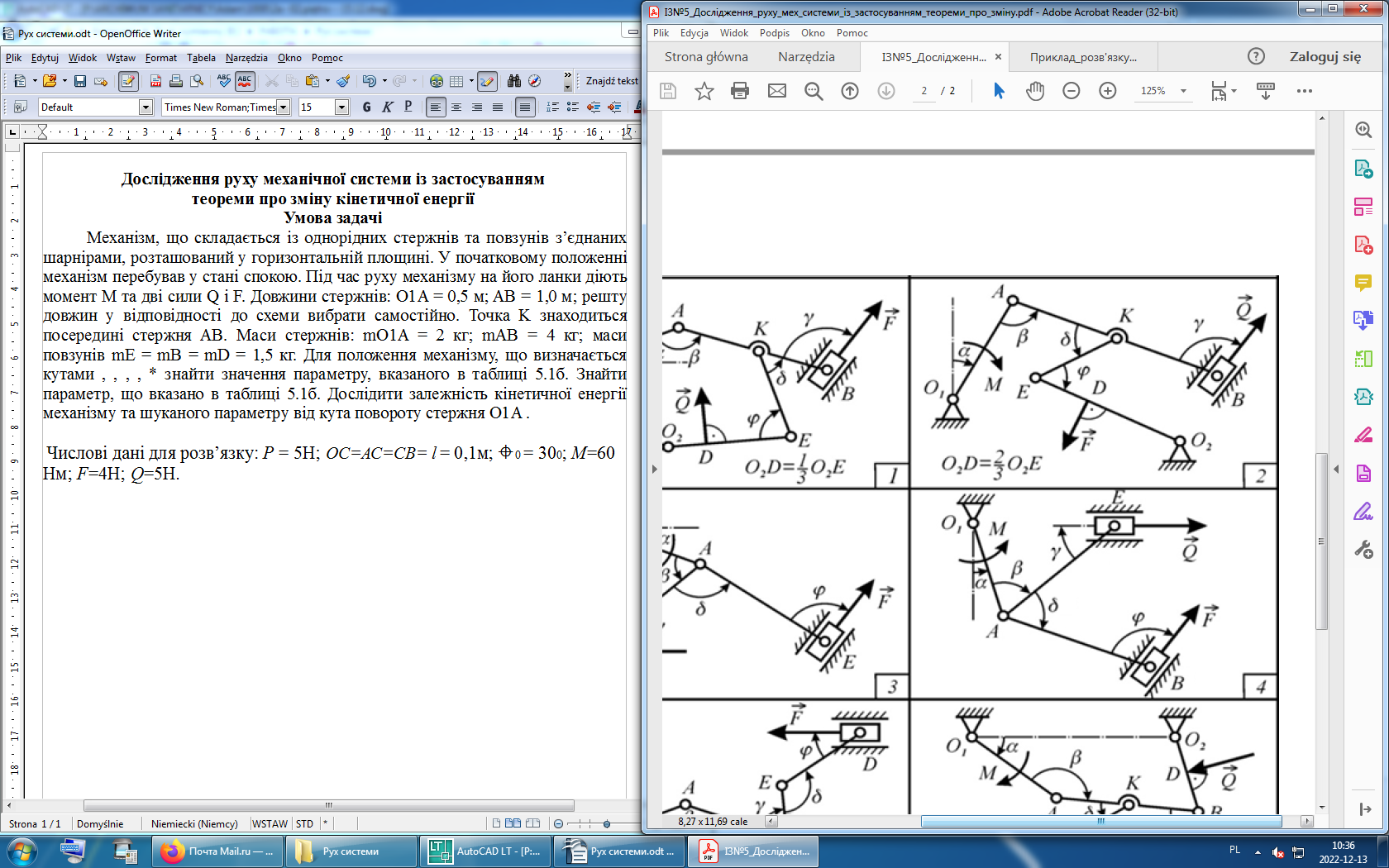


Рисунок 1 – Кінематична схема механізму
Розв’язок

1 Визначення кінетичної енергії механічної системи.

Задана механічна система складається з п’яти тіл: кривошипів 1 і 2, лінійок 3 і 4, повзуна 5. Кінетична енергія всієї системи дорівнює:

Т = Т₁ + Т₂ + Т₃ + Т₄ + Т₅

де Т₁, Т₂ - кінетична енергія кривошипів 1 і 2,

Т₃,Т₄ - кінетична енергія лінійок 3 і 4,

Т₅ - кінетична енергія повзуна 5.

Кривошипи О₁А і О₂Е здійснюють обертальний рух навколо нерухомої осі Oz, яка перпендикулярна до осі рисунка. В цьому випадку кінетична енергія тіла дорівнює



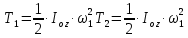
де



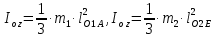
Тоді





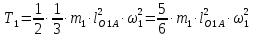
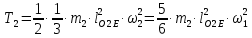
Лінійка АВ рухається плоско паралельно. Її кінетична енергія дорівнює:



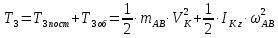
де K - швидкість точки K, яка є центром мас лінійки АВ,

ω_AB - кутова швидкість лінійки АВ,

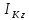- момент інерції лінійки відносно осі Kz, яка проходить через центр мас лінійки АВ.

Для визначення кутової швидкості ω_AB лінійки AB використаємо поняття миттєвого центра швидкостей. Як відомо, миттєвий центр швидкостей розташовано на перетині перпендикулярів до швидкостей двох точок тіла, що рухається плоскопаралельно. У нашому випадку швидкості точок А і В паралельні, тобто

---

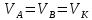. Кутова швидкість тіла ω в цей момент часу дорівнює нулю .

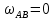З другого боку, точка A належить ланці О₁А і її швидкість дорівнює:





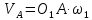
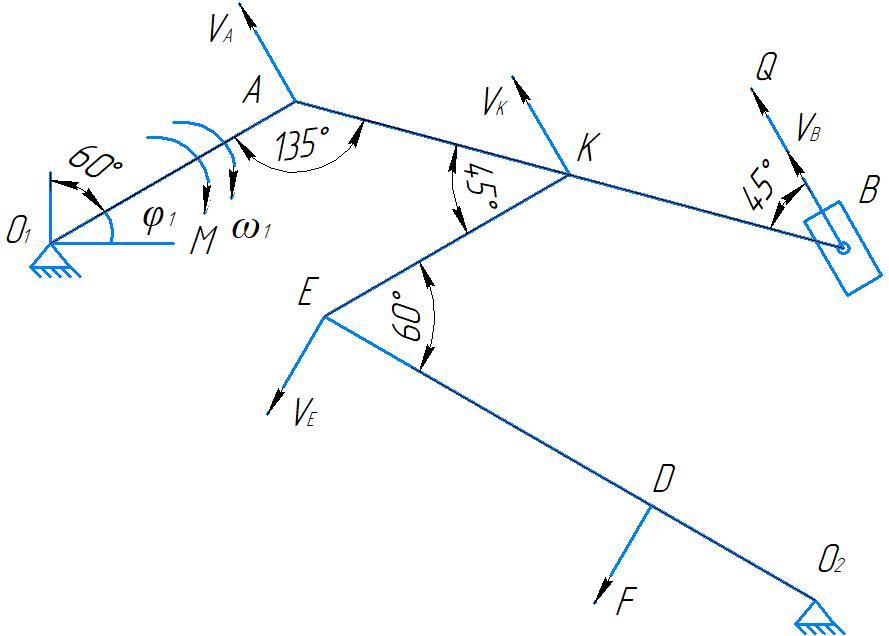
Рисунок 2 – Кінематична схема механізму з векторами та напрямами кінематичних і силових параметрів
З урахуванням одержаних значень, кінетична енергія лінійки дорівнює:



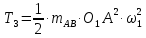
Лінійка ЕК рухається плоско паралельно. Її кінетична енергія дорівнює:



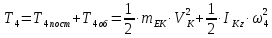
Використовуючи поняття миттєвого центра швидкостей маємо, що МЦШ лежить в точці Е. Таким чином, швидкість точки Е дорівнює:



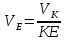
З другого боку, точка Е належить ланці О₂Е і її швидкість дорівнює:



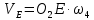
Тоді отримуємо



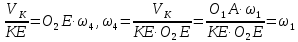
Момент інерції лінійки відносно осі Кz дорівнює:



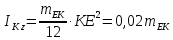
З урахуванням одержаних значень, кінетична енергія лінійки КЕ дорівнює:



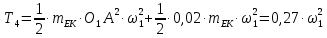
Підрахуємо кінетичну енергію повзуна В, який рухається поступально:



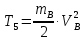
Через те, що 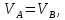отримаємо: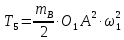



Підставляючи знайдені вирази, одержимо:





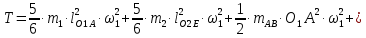
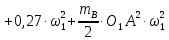
або



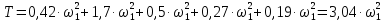
2 Визначення роботи силових факторів.

Інтегруючи за часом залежності для швидкостей точок А і В повзунів, визначаємо їх переміщення:

---

S_B = φ₁ × ВК = 0,5 φ₁

S_D = φ₁ × О₂D = 0,33 φ₁

Визначаємо роботу крутного моменту М та двох зосереджених сил F і Q при повороті кривошипа від початкового положення ОС на кут 0 j :

A(M) = M × φ₁ = 60φ₁ Дж;

A(Q) = - Q × S_B = - Q × 0,5 × φ₁ = - 5 × 0,5 × φ₁ = - 2,5 φ₁ Дж;

A(F) = F × S_D = F × 0,33 × φ₁ = 4 × 0,33 × φ₁ = 1,32 φ₁ Дж.

Просумувавши, отримаємо суму робіт усіх зовнішніх сил:



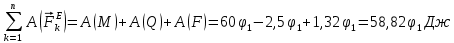
3 Теорема про зміну кінетичної енергії механічної системи має наступний вигляд:



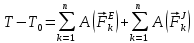
де Т – кінетична енергія системи в кінцевий (поточний) момент часу;

де Т₀ – кінетична енергія системи в початковий момент часу;

– сума робіт усіх зовнішніх сил;

– сума робіт усіх внутрішніх сил.

Оскільки у початковий момент часу система знаходилася у стані спокою, а стержні системи є абсолютно жорсткими, то:



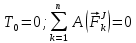
Таким чином, підставивши (6) і (10) у (11), отримаємо:



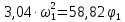
Звідси визначаємо кутову швидкість кривошипа 1:



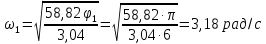
Для визначення кутового пришвидшення кривошипа 1 продиференціюємо рівняння по часу t:



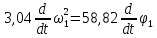
Враховуючи, що 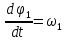, надалі матимемо: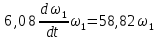



Звідси отримаємо:



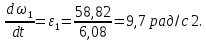
Відповідь: 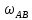= 0;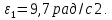

4 Дослідження залежності кінетичної енергії T механізму та кутової швидкості кривошипа 1 від кута його повороту

На основі (13) і (6) маємо:

---

,

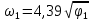
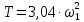
Кут одного повного оберту кривошипа 1: 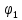= 0…360⁰.
Таблиця 5.1 – Числові значення кута повороту кривошипа 1, його кутової швидкості та кінетичної енергії механізму

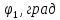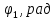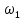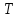0	0	0	0
30	0,523	3,18	3,1
60	1,047	4,49	6,1
90	1,570	5,50	9,2
120	2,093	6,35	12,3
150	2,617	7,10	15,3
180	3,140	7,78	18,4
210	3,663	8,40	21,5
240	4,187	8,98	24,5
270	4,710	9,53	27,6
300	5,233	10,04	30,7
330	5,757	10,53	33,7
360	6,280	11,00	36,8

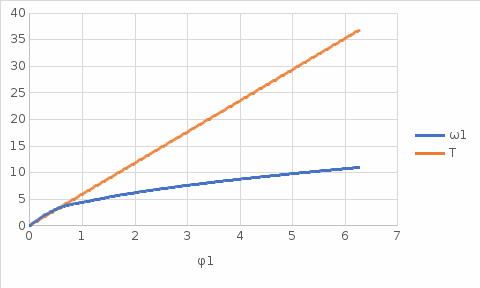
Рисунок 3 – Залежність кінетичної енергії механізму та кутової

швидкості кривошипа 1 від його кута повороту

---

Смотрите также файлы

• 1. Понятие миграции населения Классификации миграции населения.docx

• 3. Особенности промышленного переворота в России. Экономические и социальные последствия промышленного переворота.docx

• Название страны и состав территории.docx

• Приложение 3 Рецензия на индивидуальный проект.pdf

• Название страны и состав территории.docx