ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 9
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Аксиома параллельных прямых
Через точку, не лежащую на прямой, можно провести не более одной прямой, параллельной данной.
Теорема
Две прямые, параллельные третьей, параллельны.
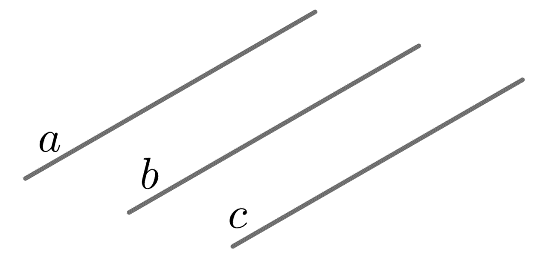
Пусть a||b и b||c . Допустим, что прямые a и b не являются параллельными (см. рисунок 4). Тогда они пересекаются в некоторой точке c .
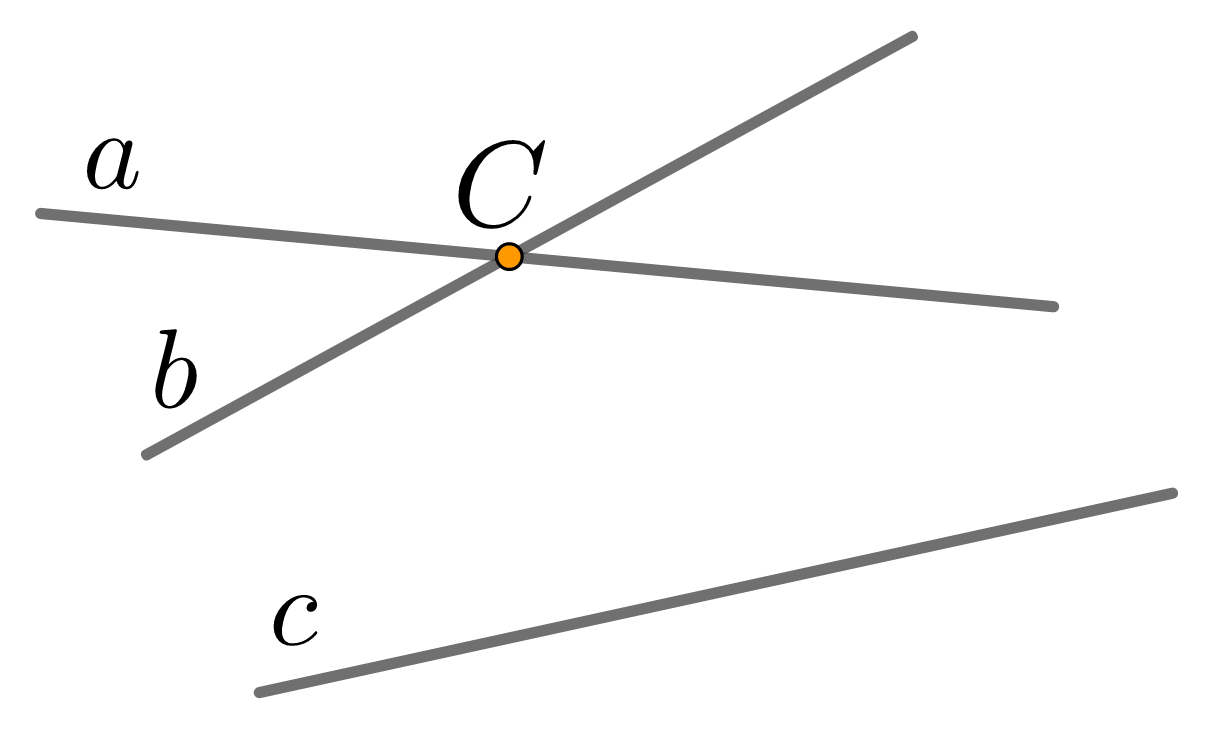
Рис. 4
Следовательно, через точку c проходит две прямые, параллельные прямой c, что противоречит аксиоме параллельности. Значит, утверждение теоремы верно.
Следствия из аксиомы параллельных прямых
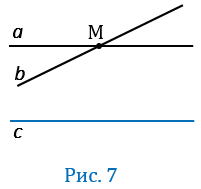
| 10. Если прямаяпересекает одну из двух параллельных прямых, то она пересекает и другую. |
Дано:
, 
= М (Рис.4).Доказать:
.
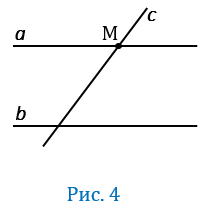
Если мы предположим, что прямая
не пересекает прямую 
, то прямая будет параллельна прямой , а по условию через точку М проходит прямая 
параллельная прямой , значит получим, что
через точку М будут проходить две прямые
и 
параллельные прямой 
(Рис.5).
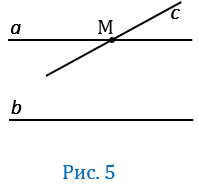
Но это противоречит аксиоме параллельных прямых, значит, наше предположение неверно, и прямая
пересекает прямую , т.е. 
. Что и требовалось доказать.| 20. Если две прямые параллельны третьей прямой, то они параллельны. |
Дано:
, 
(Рис.6).Доказать:
.Доказательство:
Предположим, что прямые
и не параллельны, т.е. пересекаются в некоторой точке М (Рис.7).
Тогда получим, что через точку М проходят
две прямые
и параллельные прямой , т.к. по условию 
и 
. Но это противоречит аксиоме параллельных прямых, следовательно, наше предположение неверно, значит, прямые и параллельны, т.е. . Что и требовалось доказать.Задача
Третье следствие всегда доказывается учениками как задача. Итак, необходимо доказать, что если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и второй.
Проведем две параллельные прямые а и b. Прямая с перпендикулярна прямой а. Это значит, что прямая с пересекает прямую а, то есть по следствия 2 из аксиомы о параллельности прямых, прямая с пересечет и прямую b, так как b и а параллельны.
Обратим внимание на углы 1 и 2 – они являются односторонними при параллельных прямых а и b, и секущей с. Значит, сумма этих углов должна равняться 180 градусам по свойству параллельных прямых. Но угол 1 известен, так как а перпендикулярна с, то угол равен 90 по определению перпендикулярности.
Найдем угол 2.
<1+<2=180
<1=90
<2=180−<1
<2=180−90=90
Значит, прямая с перпендикулярна прямой b по определению перпендикулярности.
Этим следствием можно пользоваться так же, как и остальными, но и забывать о том, что оно не является следствием в полном смысле этого слова не нужно.
Признаки параллельности двух прямых:
1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.
2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.
№ 213
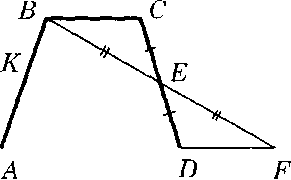
Дано: СЕ = ЕД, BE= EF,
KE ǁ AD.
Доказать: KE ǁ BC.
Доказательство: Рассмотрим
и 
.СЕ = ЕД, BE= EF, по условию.
∠ВЕС = ∠DEF как вертикальные. Значит,
= по двум сторонам и углу между ними.Тогда ∠CBE =∠EFD как соответственные в равных треугольниках. Но ∠CBE и ∠EFD накрест лежащие при прямых BC и AF
и секущей BF. Значит, BC ǁ AF.
Итак, BC ǁ AF, т. е. BC ǁ AD по доказанному,
KE ǁ AD по условию. Значит, KE ǁ BC по следствию 2 из аксиомы параллельных прямых, что требовалось доказать.
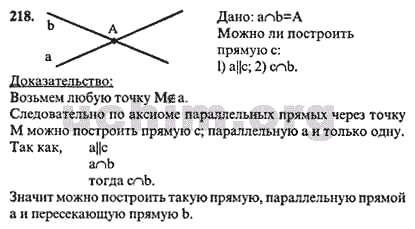
№ 219
Дано: с∩а, с∩b с- любая. Доказать: aǁb.
Доказательство: Пусть а не параллельна b. Проведём прямую с ǁ b; с∩а, но с не пересекает b (по построению), а это противоречит условию. Следовательно, a ǁ b, что и требовалось доказать.
Решение задачи № 211 (в)
Дано: а || в; с - секущая, AM - биссектриса ΔДАК; ДВ - биссектриса ∠АДМ.
Доказать: AM ⊥ ДВ.
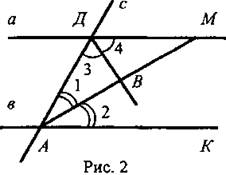
Доказательство: По условию AM — биссектриса угла ДАК, тогда ∠1 = ∠2, но ∠2 = ∠5 (внутренние накрест лежащие углы при параллельных прямых a || в и секущей AM).
Значит, ∠1 = ∠5, следовательно, треугольник АДМ - равнобедренный по признаку равнобедренного треугольника. По условию ДВ - биссектриса угла АДМ, тогда и ДВ - биссектриса равнобедренного треугольника АДМ, проведенная к основанию AM, следовательно, ДВ - высота равнобедренного треугольника АДМ, поэтому ДВ ⊥ АМ.
3. Устно по готовому чертежу на доске (см. рис. 3) решить № 220.
Решение:
Пусть при пересечении двух прямых а ив секущей накрест лежащие углы 1 и 2 не равны: ∠1 ≠ ∠2. Предположим, что прямые а и в параллельны. Тогда согласно свойству параллельных прямых ∠1 = ∠2, что противоречит условию задачи. Значит, наше предположение неверно и прямые а и в пересекаются.
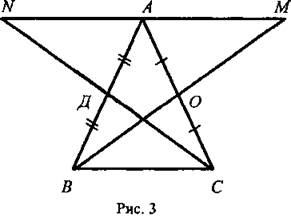
4. Решить задачу № 221.
Решение: Пусть О и Д — середины сторон АС и АВ. Треугольники АОМ и СОВ равны по двум сторонам и углу между ними (АО = ОС, ВО = ОМ, ∠АОМ = ∠СОВ), поэтому ∠АОМ = ∠СВО, значит, AM || ВС. Аналогично ΔANД = ΔВСД, и, значит, AN || ВС. Итак, через точку А можно провести только одну прямую, параллельную ВС. Следовательно, прямые AM и AN совпадают, то есть точки М, А и N лежат на одной прямой.