Практическая работа №13.

Определение основных характеристик электрического поля.
1. Потенциальная энергия заряженного тела в однородном электростатическом поле.

Понятие потенциальной энергии самое сложное в электростатике. Вспомните, как нелегко было представить себе, что такое потенциальная энергия в механике. Силу мы ощущаем непосредственно, а потенциальную энергию нет. На пятом этаже дома потенциальная энергия нашего тела больше, чем на первом. Но мы это никак не воспринимаем. Различие становится понятным, если вспомнить, что при подъеме вверх пришлось совершить работу, а также если представить себе, что произойдет при падении с пятого этажа.

Энергия взаимодействия электронов с ядром в атоме и энергия взаимодействия атомов друг с другом в молекулах (химическая энергия) – это в основном электрическая энергия. Огромная электрическая энергия запасена внутри атомного ядра. Именно за счет этой энергии выделяется теплота при работе ядерного реактора атомной электростанции.

С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом. При перемещении заряда действующая на него со стороны поля сила совершает работу. Поэтому можно утверждать, что заряженное тело в электрическом поле обладает энергией. Найдем потенциальную энергию заряда в однородном электрическом поле.

Работа при перемещении заряда в однородном электростатическом поле. Однородное поле создают, например, большие металлические пластины, имеющие заряды противоположного знака. Это поле действует на заряд с постоянной силой 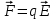, подобно тому как Земля действует с постоянной силой 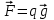на камень вблизи ее поверхности. Пусть пластины расположены вертикально (рис.1), левая пластина В заряжена отрицательно, а правая D – положительно. Вычислим работу, совершаемую полем при перемещении положительного заряда q из точки 1, находящейся на расстоянии d₁ от пластины В, в точку 2, расположенную на расстоянии d₂1 от той же пластины. Точки 1и 2 лежат на одной силовой линии.

На участке пути 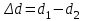электрическое поле совершит положительную работу:

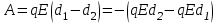. (1)



- +







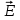
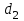
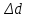
2 1




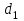
В D

(рис.1)

Эта работа не зависит от формы траектории, подобно тому как не зависит от формы траектории работа силы тяжести. Докажем это непосредственным расчетом.

Потенциальная энергия. Если работа не зависит от формы траектории, то она равна изменению потенциальной энергии, взятому с противоположным знаком:

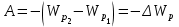. (2)

Сравнивая полученное выражение (1) с общим определением потенциальной энергии (2), видим, что потенциальная энергия заряда в однородном электростатическом поле равна:






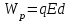
(3)
Формула (3) побочна формуле 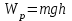для потенциальной энергии тела над поверхностью Земли. Но заряд q в отличие от массы может быть как положительным, так и отрицательным.

На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю:

.
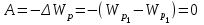2. Потенциал электростатического поля и разность потенциалов.

В механике взаимное действие тел друг на друга характеризуют силой или потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряженность поля – это силовая характеристика. Теперь введем энергетическую характеристику – потенциал.

Потенциал поля. Работа любого электростатического поля при перемещении в нем заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля. На замкнутой траектории работа электростатического поля всегда равна нулю. Поля, обладающие таким свойством, называют потенциальными. Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.

Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула 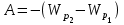справедлива для любого электростатического поля. И только в случае однородного поля потенциальная энергия выражается формулой (3).

Потенциал. Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля, так и для любого другого. Следовательно, отношение потенциальной энергии к заряду не зависит от помещенного в поле заряда.

Это позволяет ввести новую количественную характеристику поля – потенциал, не зависящую от заряда, помещенного в поле.

Потенциалом электростатического поля называют отношение потенциальной энергии заряда в поле к этому заряду.

Согласно данному определению потенциал равен:

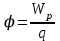. (4)

Напряженность поля 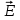является вектором и представляет собой силовую характеристику поля; она определяет силу, действующую на заряд q в данной точке поля. Потенциал 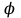- скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.

Если в качестве нулевого уровня потенциальной энергии, а значит, и потенциала принять отрицательно заряженную пластину, то согласно формулам (3) и (4) потенциал однородного поля равен:

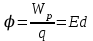. (5)

Разность потенциалов. Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Практическое значение имеет не сам потенциал в точке, а изменение потенциала, которое не зависит от выбора нулевого уровня отсчета потенциала.

Так как потенциальная энергия 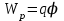, то работа равна:

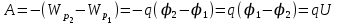. (6)

Здесь

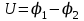(7)

разность потенциалов, т.е. разность значений потенциала в начальной и конечной точках траектории.

Разность потенциалов называется также напряжением.

Согласно формулам (6) и (7) разность потенциалов оказывается равной:

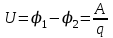. (8)

Единица разности потенциалов. Единицу разности потенциалов устанавливают с помощью формулы (8). В Международной системе единиц работу выражают в джоулях, а заряд - в кулонах. Поэтому разность потенциалов между двумя точками равна единице, если при перемещении зарядов в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В); 1 В = 1 Дж/1 Кл.
3. Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности.

Пусть заряд q перемещается в направлении напряженности однородного электрического поля 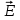из точки 1 в точку 2, находящуюся на расстоянии 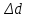от точки 1 (рис.2). Электрическое поле совершает работу:

.




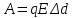1 2


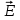
(рис.2)
Эту работу согласно формуле (8) можно выразить через разность потенциалов в точках 1 и 2:

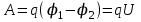. (9)

Приравнивая выражения для работы, найдем модуль вектора напряженности поля:





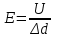
(10)
В этой формуле U - разность потенциалов между двумя точками 1 и 2, которые связаны вектором перемещения , совпадающим по направлению с вектором напряженности 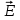(см. рис.2).

Формула (10) показывает: чем меньше меняется потенциал на расстоянии 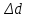, тем меньше напряженность электростатического поля; если потенциал не меняется совсем, то напряженность поля равна нулю.

Так как при перемещении положительного заряда в направлении напряженности 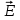электростатическое поле совершает положительную работу 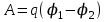, то потенциал 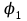больше потенциала .

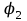Следовательно, напряженность электрического поля направлена в сторону убывания потенциала.

Единица напряженности электрического поля. Единицу напряженности электрического поля в СИ устанавливают, используя формулу (10). Напряженность электрического поля равна единице, если разность потенциалов между двумя точками на расстоянии 1 м в однородном поле равна 1 В.Наименование этой единицы – вольт на метр (В/м).

Напряженность можно также выражать в ньютонах на кулон. Действительно,

.

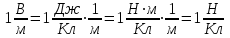Эквипотенциальные поверхности. При перемещении заряда под углом 90⁰ к силовым линиям электрическое поле не совершает работы, так как сила перпендикулярна перемещению. Значит, если провести поверхность, перпендикулярную в каждой точке силовым линиям, то при перемещении заряда вдоль этой поверхности работа не совершается.

А это означает, что все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же потенциал.

Поверхности равного потенциала называют эквипотенциальными.

Эквипотенциальные поверхности однородного поля представляют собой плоскости, а поля точечного заряда – концентрические сферы.

Подобно силовым линиям, эквипотенциальные поверхности качественно характеризуют распределение поля в пространстве. Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.

Эквипотенциальной является поверхность любого проводника в электростатическом поле. Ведь силовые линии перпендикулярны поверхности проводника. Причем не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряженность поля внутри проводника равна нулю, значит, равна нулю и разность потенциалов между любыми точками проводника.
Задание 1.Прочитать лекцию урока, посмотреть презентацию и сделать конспект лекции в тетради.
Задание 2. Ответить на тестовые вопросы на сайте по данной теме.
Задание 3. Решить задачу.

Какую работу совершает поле при перемещении заряда 5нКл из точки с потенциалом 300 В в точку с потенциалом 100В?
Дескрипторы:

1. 
   Записывает ДАНО
   
2. 
   Переводит в СИ
   
3. 
   Использует верные формулы
   
4. 
   Решает задачу.
   

Чек лист к уроку №32.

Буквенный эквивалент	Оценка по традиционной системе	Процентное содержание баллов	Задания
А	«Отлично»	95-100	Задание 1,2,3выполнены
А-		90-94	Задание 1,2выполнены + Задание 3 выполнено
В+	«Хорошо»	85-89	Задание 1 выполнено + Задание 2выполнено 70-89 % выполнения
В		80-84
В-		75-79
С+		70-74
С	«Удовлетво-рительно»	65-69	Задание 1выполнено 50-69 % выполнения
С-		60-64
D+		55-59
D		50-54
F	«Неудовлет-ворительно»	0-49

---

Смотрите также файлы

• Аналитикалы геометрия жне сызыты алгебра.doc

• Хронологическая таблица правления казахских ханов в xvxix вв.docx

• Задание Вставьте, где необходимо, подходящий артикль к именам собственным.docx

• К какому контингенту обследуемых относится больная.docx

• "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса алХорезми.docx