Файл: Исследование статистических характеристик случайных факторов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.04.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Д.27.03.03-САУ-18.21/6096-ЛР Кафедра искусственного интеллекта и системного анализа
Лабораторная работа №1
по дисциплине «Моделирование сложных систем»
тема: «Исследование статистических характеристик случайных факторов»
Проверил:
__________ ст.преп. Ю.К. Орлов
(дата, подпись)
__________ acc. А.В. Левкина
(дата, подпись)
Выполнил:
__________ ст.гр. САУ-18 Д.О. Шапошник
(дата, подпись)
Донецк-2021
1 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Цель работы: приобретение практических навыков исследования статистических характеристик случайных факторов.
-
Краткие теоретические сведения
Закон распределения полностью характеризует случайную величину (с.в.). Однако при решении многих практических задач достаточно знать лишь некоторые числовые параметры, характеризующие отдельные существенные свойства (черты) закона распределения с.в. Такие числа принято называть числовыми характеристиками с.в. Важнейшими среди них являются характеристики положения: математическое ожидание (центр распределения с.в.), мода, медиана; характеристики рассеяния: дисперсия (отклонение значений с.в. от ее центра), среднеквадратическое отклонение.
Для того чтобы составить общее представление о законе распределения с.в. X, незачем фиксировать каждое наблюденное значение и строить статистическую функцию распределения F*(x). Этим целям лучше служат группированный статистический ряд и гистограмма. Для построения группированного статистического ряда весь участок оси абсцисс, на котором расположены значения с.в. X, наблюдавшиеся в опыте, разделяют на участки или «разряды». Длины разрядов необязательно брать равными друг другу: бывают случаи, когда на тех участках оси абсцисс, где наблюденные значения X располагаются гуще, удобнее брать разряды более мелкими, а там, где реже, – более крупными (или объединять два или более равных по длине разрядов в один). Границы разрядов удобно принимать «круглыми» числами.
2 РУЧНОЙ ПРОСЧЕТ
Исходная выборка
6.920 9.098 7.928 7.633 7.759 4.264 6.337 7.517 7.952 8.406 8.548 7.563 7.608 8.004 7.628 8.233 9.175 7.498 8.860 6.620 8.224 10.670 6.233 8.585 9.693 10.862 7.958 8.142 5.847 8.048 8.451 7.563 8.811 9.788 9.342 8.893 4.625 6.375 9.133 7.371 7.599 10.253 7.228 11.708 7.094 5.871 7.102 9.440 7.675 8.154 7.513 7.649 6.030 9.237 8.096 6.287 8.607 7.492 8.545 9.443 8.184 7.962 8.313 9.410 8.088 10.849 8.224 8.690 6.738 4.675 8.439 9.262 9.040 8.471 6.950 7.909 9.197 9.159 6.898 5.922 8.693 8.933 10.566 6.858 5.684 8.034 5.562 6.493 8.470 8.821 9.742 6.863 9.306 7.895 8.542 10.030 5.836 8.148 9.255 6.830
Так как просчитать вручную все элементы затруднительно то возьмем первые 20
6.920 9.098 7.928 7.633 7.759 4.264 6.337 7.517 7.952 8.406 8.548 7.563 7.608 8.004 7.628 8.233 9.175 7.498 8.860 6.620
Составим таблицу
| X | |X-Xср| | (X-Xср)^2 |
| 4,264 | 3,75729 | 14,11723 |
| 6,337 | 1,68429 | 2,836833 |
| 6,62 | 1,40129 | 1,963614 |
| 6,92 | 1,10129 | 1,21284 |
| 7,498 | 0,52329 | 0,273832 |
| 7,517 | 0,50429 | 0,254308 |
| 7,563 | 0,45829 | 0,21003 |
| 7,608 | 0,41329 | 0,170809 |
| 7,628 | 0,39329 | 0,154677 |
| 7,633 | 0,38829 | 0,150769 |
| 7,759 | 0,26229 | 0,068796 |
| 7,928 | 0,09329 | 0,008703 |
| 7,952 | 0,06929 | 0,004801 |
| 8,004 | 0,01729 | 0,000299 |
| 8,233 | 0,21171 | 0,044821 |
| 8,406 | 0,38471 | 0,148002 |
| 8,548 | 0,52671 | 0,277423 |
| 8,86 | 0,83871 | 0,703434 |
| 9,098 | 1,07671 | 1,159304 |
| 9,175 | 1,15371 | 1,331047 |
Найдем показатели центра распределения
Простая средняя арифметическая X = Сумма x / n = 7.67755
Мода x = 7.6
Медиана n/2 = 20 / 2 =10
Ранжированный ряд включает четное число единиц, следовательно, медиана определяется как средняя из двух центральных значений: (7.633+7.759)/2=7.696
Показатели вариации
Абсолютные показатели вариации
Размах вариации – разновидность между максимальными и минимальными значениями признака первичного ряда.
R = Xmax-Xmin= 9,175-4,264 = 4.911
Дисперсия
D = (8.02129-7.67755) / 20 = 0.017187
Среднее квадратическое отклонение (средняя ошибка выборки)
Гамма = корень из D = 0.13
Каждое значение ряда отличается от среднего значения 7.696 в среднем на 0.13
3 ТЕКСТ ПРОГРАММЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
fprintf('Лабораторная работа №1')
fprintf('\n')
sf=[6.920; 9.098; 7.928; 7.633;7.759;4.264;6.337;7.517;7.952;8.406;
8.548;7.563;7.608;8.004;7.628;8.233;9.175;7.498;8.860;6.620;
8.224;10.670;6.233;8.585;9.693;10.862;7.958;8.142;5.847;8.048;
8.451;7.563;8.811;9.788;9.342;8.893;4.625;6.375;9.133;7.371;
7.599;10.253;7.228;11.708;7.094;5.871;7.102;9.440;7.675;8.154;
7.513;7.649;6.030;9.237;8.096;6.287;8.607;7.492;8.545;9.443;
8.184;7.962;8.313;9.410;8.088;10.849;8.224;8.690;6.738;4.675;
8.439;9.262;9.040;8.471;6.950;7.909;9.197;9.159;6.898;5.922;
8.693;8.933;10.566;6.858;5.684;8.034;5.562;6.493;8.470;8.821;
9.742;6.863;9.306;7.895;8.542;10.030;5.836;8.148;9.255;6.830]
x=sort(sf(:));
n=length(x);
xmin=x(1);
xmax=x(n);
fprintf('\n')
fprintf('Обьем выборки n=%d\n',length(x))
fprintf('xmin=%14.7f\n',xmin)
fprintf('xmax=%14.7f\n',xmax)
fprintf('\n')
Mx=mean(x);Sx=std(x);Dx=Sx^2;
Ax=sum((x-Mx).^3)/(n-1)/Sx^3;
Ex=sum((x-Mx).^4)/(n-1)/Dx^2-3;
disp('Выборочные параметры распределения:')
fprintf('Математическое ожидание Mx=%14.7f\n',Mx)
fprintf('Среднеквадратичное отклонение Sx=%14.7f\n',Sx)
fprintf('Дисперсия Dx=%14.7f\n',Dx)
fprintf('Асимметрия Ax=%14.7f\nЭксцесс Ex=%14.7f\n',Ax,Ex)
k=7;
Лабораторная работа №1
sf =
6.9200
9.0980
7.9280
7.6330
7.7590
4.2640
6.3370
7.5170
7.9520
8.4060
8.5480
7.5630
7.6080
8.0040
7.6280
8.2330
9.1750
7.4980
8.8600
6.6200
8.2240
10.6700
6.2330
8.5850
9.6930
10.8620
7.9580
8.1420
5.8470
8.0480
8.4510
7.5630
8.8110
9.7880
9.3420
8.8930
4.6250
6.3750
9.1330
7.3710
7.5990
10.2530
7.2280
11.7080
7.0940
5.8710
7.1020
9.4400
7.6750
8.1540
7.5130
7.6490
6.0300
9.2370
8.0960
6.2870
8.6070
7.4920
8.5450
9.4430
8.1840
7.9620
8.3130
9.4100
8.0880
10.8490
8.2240
8.6900
6.7380
4.6750
8.4390
9.2620
9.0400
8.4710
6.9500
7.9090
9.1970
9.1590
6.8980
5.9220
8.6930
8.9330
10.5660
6.8580
5.6840
8.0340
5.5620
6.4930
8.4700
8.8210
9.7420
6.8630
9.3060
7.8950
8.5420
10.0300
5.8360
8.1480
9.2550
6.8300
3.1 Результат работы программы
Обьем выборки n=100
Xmin = 4.2640000
xmax =11.7080000
Выборочные параметры распределения:
Математическое ожидание Mx= 8.0212900
Среднеквадратичное отклонение Sx=1.3893423
Дисперсия Dx = 1.9302721
Асимметрия Ax = -0.1853395
Эксцесс Ex = 0.2391981
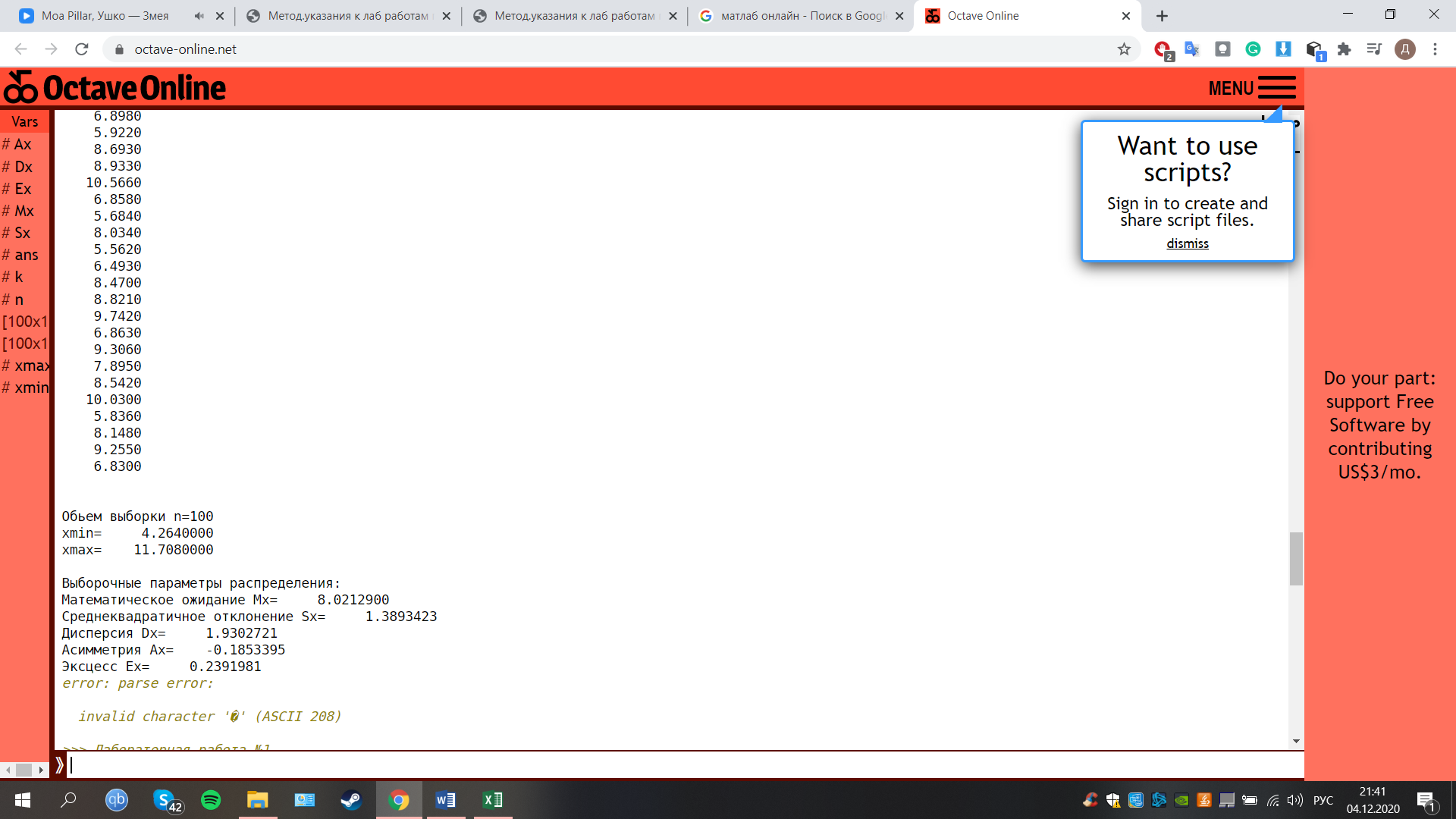
Рис 3.1 – Результат работы программы в онлайн сервисе OctaveOnline (бесплатная альтернатива MATLAB)

