Тема лекции №2: Проблемы оптимизации сложных систем и процессов в ИСО. Решение задач линейного программирования.

Количество часов: 1 час

Цель:

1. 
   Графический метод решения задач линейного программирования
   
2. 
   Формы записи задач (ЗЛП)
   
3. 
   Основы симплекс-метода
   
4. 
   Алгоритм симплекс метода
   
5. 
   Поиск начального базиса
   

Графический метод решения задач линейного программирования Графический метод применяют, когда число переменных не превосходит 2. На практике задачи такой размерности встречаются редко, однако графический метод хорошо иллюстрирует основные понятия, используемые при решении ЗЛП большой размерности. Графический метод рассмотрим на примере задачи 5 (задача технического контроля) Пример



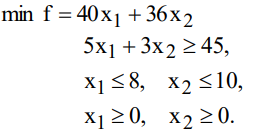
В качестве первого шага решения следует определить допустимую область или область допустимых решений (ОДР). Для изображения ОДР следует начертить графики всех ограничений.

Все допустимые решения лежат в первом квадранте, т.к. x1 , x2  0 (см. рис. 2.1) ОДР является треугольник ABC (в общем случае многогранник M при m 2 ), который содержит бесконечное число допустимых точек. Нужно найти точку, в которой fx  min .

Если зафиксировать значение ЦФ то соответствующие ему точки будут лежать на некоторой прямой. При изменении величины f прямая подвергается параллельному переносу. Рассмотрим прямые, соответствующие различным значениям f , имеющие с ОДР хотя бы одну общую точку. Положим f0  680 . Тогда прямая ЦФ пройдет через точку B8,10 . При приближении прямой ЦФ к началу координат значение f уменьшается. Минимальное значение ЦФ достигается в узловой точке A8, 5/3. Следовательно, x ^  8, 5/3; f^  380 - оптимальное решение задачи. Таким образом x^ 8, 5/3 - оптимальный план.



Итак, для оптимального режима работы ОТК необходимо использовать 8 контролеров 1-го разряда и 1,6 контролера 2-го разряда. Дробное значение x2 1.6 соответствует ситуации, когда один из двух К2 используется в течении неполного рабочего дня. При недопустимости неполной загрузки контролеров дробные значения обычно округляются, получая приближенное оптимальное целочисленное решение x1  8, x2  2.

---

Итак, мы рассмотрели линейные уравнения и неравенства с двумя переменными. Если перейти к линейным зависимостям с тремя переменными, то тогда они будут описывать плоскость в трехмерном пространстве; линейное неравенство характеризует полупространство, а система линейных неравенств — многогранник как область допустимых решений в трехмерном пространстве.

С увеличением числа переменных выше трех, геометрическая интерпретация невозможна, так как система неравенств определяет область допустимых решений в k - мерном пространстве. При этом мерность пространства определяют так: если ограничения заданы неравенствами, то k  n , где n — число переменных; если ограничения в виде уравнений, то k  n  m, где m — число уравнений. Из рассмотренного примера решения задачи ОТК мы видели, что оптимальное решение задачи соответствует одной из вершин многогранника.

• Отсюда можно сделать исключительно важный вывод: оптимальное решение — координаты вершины области допустимых решений.

Из этого вывода следует метод решения задач линейного программирования, который заключается в следующем:

1. Найти вершины области допустимых решений как точки пересечения ограничений.

2. Определить последовательно значения целевой функции в вершинах.

3. Вершина, в которой целевая функция приобретает оптимальное (max или min) значение, является оптимальной вершиной.

4. Координаты оптимальной вершины есть оптимальные значения искомых переменных.

Формы записи задач (ЗЛП)







Теорема 1. Множество всех решений ЗЛП выпукло.

Теорема 2 . Линейная форма fx c ^t x  ЗЛП достигает своего минимума (максимума) в крайней точке выпуклой области решений S (в вершине многогранника). Если fx достигает min max  более, чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся выпуклой комбинацией этих точек.

---

Основы симплекс-метода

Рассмотрим общую ЗЛП с m ограничениями и n переменными, записанную в стандартной (канонической) форме



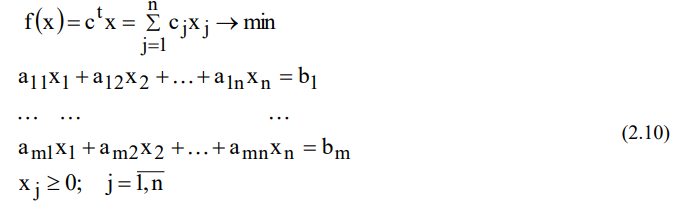
Как правило, число уравнений задачи меньше числа переменных ( т.е. m  n ), поэтому множество ее допустимых решений равно  . Задача состоит в том, чтобы найти наилучшее решение в смысле принятого критерия (минимума целевой функции).

Из теоремы 2 следует, что оптимальное решение представляет собой одну из вершин многогранника допустимой области. Другими словами, оптимальное решение это одно из базисных решений.

Получение одного из базисных решений основано на известном классическом методе решения систем линейных уравнений – методе Гаусса – Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому или ступенчатому виду при помощи элементарных операций над строками

1) умножение любого уравнения системы на положительное или отрицательное число

2) прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число При использовании первых m переменных такая система имеет следующий вид



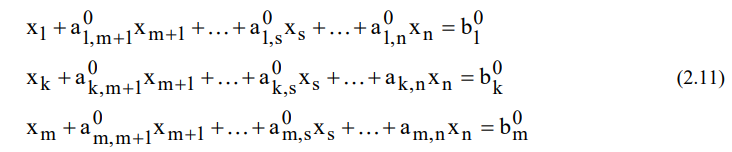
Подставляя эти переменные в целевую функцию, получим



Переменные x1 ,… , xm входящие с единичными коэффициентами в одно уравнение системы (2.11) (или (2.14)) и с нулевыми в остальные, называются базисными или зависимыми. В канонической системе (2.11), (2.14) каждому уравнению соответствует ровно одна базисная переменная.

Остальные n  m переменные x_{m+1, …,} x_n  называются небазисными или независимыми переменными.

При записи системы в каноническом виде все ее решения можно получить, присваивая независимым переменным произвольные значения и решая затем получающуюся систему относительно зависимых переменных.

Определение 4 Базисным решением системы (2.11) называется решение, полученное при нулевых значениях небазисных переменных. Например, в системе (2.11) одно из базисных решений задается как

---

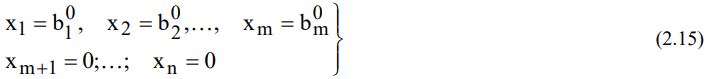
Теорема 3 (о конечности алгоритма симплекс метода). Если существует оптимальное решение ЗЛП, то существует и базисное оптимальное решение. Это решение может быть получено через конечное число шагов симплекс-методом, причем, начать можно с любого исходного базиса.

Алгоритм симплекс метода

Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц. Для удобства составления симплекс-таблицы (СТ) будем считать, что ЦФ и система ограничений переписаны в форме (2.11), (2.12)



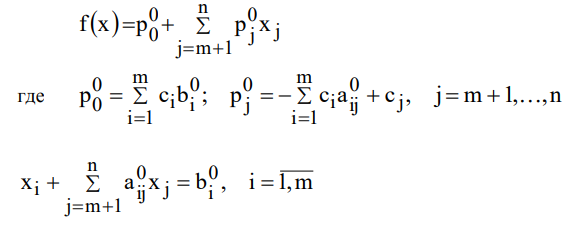
Поиск начального базиса

Для решения задачи ЛП симплексным методом, необходимо получить начальный опорный план (начальный базис).

Рассмотрим способ получения начального базиса (начальной угловой точки многогранника допустимой области). Если в исходной задаче ЛП ограничения заданы в виде неравенств, например,



то введение дополнительных переменных y₁  x_n1 , y₂  x_n2 ,...,y_m  x_nm приведет (1) к виду

---

Смотрите также файлы

• Урок астрономии Небесные координаты.doc

• 1. Антропометрия занимается изучением Размеров человеческого тела и его частей.docx

• Инструкция по выполнению контрольной работы Контрольная работа рассчитана на 45 минут и включает 15 заданий.docx

• Организация рабочих мест и совершенствование условий труда на предприятие Балтийский завод.docx

• Определение законов распределения случайных величин на основе опытных данных реферат.docx