ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Теорема. Если о > 1, то произведение чисел а и b равно сумме b слагаемых, каждое из которых равно а.
Доказательство. Обозначим сумму b слагаемых, каждое из которых равно а, через а ▫ b. И, кроме того, положим, что а ▫ 1 = а. Тогда выражение а°(b + 1) будет означать, что рассматривается сумма b + 1 слагаемого, каждое из которых равно а, т.е. а ▫( b + 1) = а + а + ...
Определение. Если а, b - целые неотрицательные числа, то произведением а ⋅ b называется число, удовлетворяющее следующим условиям:
1) а ⋅ b = а + а + ... + а + а, если b > 1;
b слаг.
-
а⋅ b = а, если b = 1; -
а⋅ b = 0, если b = 0.
Теорема 5. Пусть А и В - конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство:
n(АхВ)= п(А)⋅ п(В).
Законы умножения
Докажем законы умножения, исходя из определения произведения через декартово произведение множеств.
-
Переместительный закон: для любых целых неотрицательных чисел а и b справедливо равенство а
b=b а.
Пусть а=п(А), b=п(В). Тогда по определению произведения а
b=п (АХВ). Но множества АХВ и ВХА равномощны: каждой паре (а, b) из множества АХВ можно поставить в соответствие единственную пару (b, а) из множества ВХА, и наоборот. Значит, п(АХВ)=п (ВХА),и поэтому а b=n(АХВ)=п(ВХА)= b • а.-
Сочетательный закон: для любых целых неотрицательных чисел а, b, с справедливо равенство (а b) с = а • (b с).
Пусть а = n(A), b= п(В), с = п(С). Тогда по определению произведения (а
b) с=п((АХВ)ХС),
а а
(b с)= п(АХ(ВХС)). Множества (АХВ)ХС и АХ(ВХС) различны: первое состоит из пар вида ((а, b), с), а второе — из пар вида (а, (b, с)), где а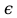
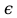A, b B, с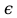 С. Но множества (АХВ)ХС и AХ(ВХС) равномощны, так как существует взаимно однозначное отображение одного множества на другое. Поэтому п((АХВ)ХС) = п (AХ(ВХС)), и, значит, (а b) с = а (b c).-
Распределительный закон умножения относительно сложения: для любых целых неотрицательных чисел а, b, с справедливо равенство (a+b) с = ас+bс.
Этот закон выводится из равенства
Пусть
. Тогда по определению произведения имеем
Откуда на основании равенства (*) получаем 
Далее по определению суммы и произведения
= п(АXС) + п (В X С) = ас + bс.-
Распределительный закон умножения относительно вычитания: для любых целых неотрицательных чисел а, b и с и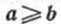
справедливо равенство (а - b)с =ас - bс.
Этот закон выводится из равенства
и доказывается аналогично предыдущему.Переместительный и сочетательный законы умножения можно распространить на любое число множителей.
Как и при сложении, эти законы часто используются совместно, т. е. произведение нескольких множителей не изменится, если их переставить любым способом и если любую их группу заключить в скобки.
Распределительные законы устанавливают связь умножения со сложением и вычитанием. На основе этих законов происходит раскрытие скобок в выражениях типа (а+b)с и (a — b)c, а также вынесение множителя за скобки, если выражение имеет вид ас — bс или ас + bс.
Деление
Рассмотрим задачу, которую решают младшие школьники. Приступая к изучению действия деления: «8 апельсинов разложили [на тарелки, по 2 апельсина на каждую. Сколько раз по 2 апельсина положили? Сколько тарелок потребовалось?»
Ответ на вопрос задачи находится при помощи деления: 8:2=4.
Проанализируем решение этой задачи. В задаче рассматривается множество, в котором 8 элементов. Оно разбивается на подмножества, в каждом из которых по 2 элемента, т. е. на. равномощные подмножества (рис. 98). Кроме того, они попарно не пересекаются. В задаче спрашивается, сколько таких подмножеств получилось. Таким образом, число 4, полученное в ответе,— , это число двухэлементных подмножеств, на которые разбито множество из 8 элементов.
В общем виде частное целого неотрицательного числа а и натурального числа b определяется следующим образом:
Определение. Пусть а = п (А) и множество А разбито на попарно непересекающиеся равномощные подмножества.
Если b — число подмножеств в разбиении множества A, то частным чисел а и b называется число элементов каждого подмножества.
Если b — число элементов каждого подмножества в разбиении множества А, то частным чисел а и b называется число подмножеств в этом разбиении.
Действие, при помощи которого находят частное а: b, называется делением, число а — делимым, b — делителем.
Определение. Частным целого неотрицательного числа а и натурального числа b называется такое целое неотрицательное число с=а:b, произведение которого и числа b равно а.
Можно показать и наличие обратной связи, т. е. что из второго определения частного вытекает первое:
Определение деления как действия, обратного умножению,
в явном виде не дается. Взаимосвязь деления и умножения устанавливается при изучении темы «Нахождение неизвестного множителя», где, по существу, происходит обобщение двух смыслов частного, имеющих место при его теоретико-множественной трактовке.
Отношения "больше в", "меньше в "
Часто при решении задач и в практической деятельности возникает вопрос: «во сколько раз одно число больше или меньше другого?» Первое знакомство с отношениями «больше в» и «меньше в» происходит в начальной школе. Уточним смысл этих отношений.
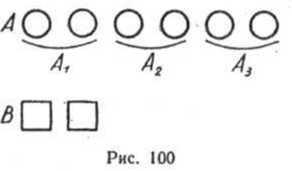
Пусть дано множество А, в котором 6 элементов, и множество В, содержащее 2 элемента. Выделим в множестве А подмножества, равномощные множеству В (рис. 100). Их оказывается 3. В этом случае говорят, что число 6 больше числа 2 в 3 раза, а число 2 меньше числа 6 в 3 раза.
Вообще если даны числа а и b, такие, что а = п (А), b = п (В),
и множество А можно разбить на с подмножеств, равномощных множеству В, то говорят, что число а больше числа b в с раз, а число b меньше числа а в с раз.Но что представляет собой это число с? С теоретико-множественной точки зрения — это частное чисел а и b. Отсюда получаем правило:
Чтобы узнать, во сколько раз одно число больше или меньше другого,, необходимо большее число разделить на меньшее.
Отношения «больше в» и «меньше в» встречаются и в задачах другого вида.
Задача. У Нины 6 тетрадей, а у Коли в 2 раза меньше. Сколько тетрадей у Коли?
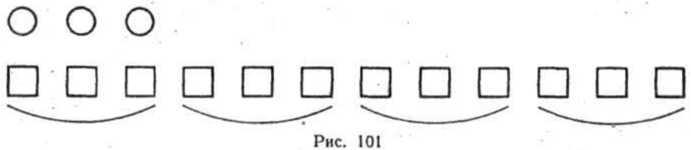
В задаче речь идет о двух множествах: множестве А тетрадей у Нины и множестве В тетрадей у Коли. Известно, что п (А) = 6. Требуется найти п (В), зная, что это число в 2 раза меньше числа 6. Исходя из этого условия множество А можно представить состоящим из двух равномощных подмножеств (рис. 102), и тогда в множестве В будет столько элементов, сколько в каждом подмножестве множества А, число которых находится делением: 6:2 = 3. Значит, n (В)= 3, т. е. у Коли 3 тетради.
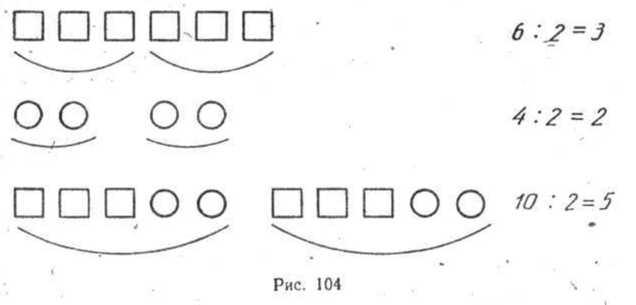
Правила деления суммы на число и числа на произведение
Правило деления суммы на число. Если числа aub делятся на число с, то и их сумма a+b делится на с; частное, получаемое при делении суммы а+ b на число с, равно сумме частных, получаемых при делении а на с и b на с, т. е.
(а+ b):с=а:с+ b:с.
Правило деления числа на произведение. Если натуральное число а делится на натуральные числа b и с, то, чтобы разделить а на произведение чисел b и с, достаточно разделить число а на b(с) и полученное частное разделить на с (b): a:(b •c)=(a:b)\c=(a:c):b.
Правило умножения числа, на частное двух чисел. Чтобы умножить число на частное двух чисел, достаточно умножить это число на делимое и полученное произведение разделить на делитель, т. е.
a-(b:c) = (a-b):c.
Деление с остатком
Число 37 не делится на 8. Но существуют числа 4 и 5, такие, что 37 = 8-4 + 5. Говорят, что деление числа 37 на 8 выполнено с остатком, при этом найдено неполное частное 4 и остаток 5.
Определение. Разделить с остатком целое неотрицательное число а на натуральное число 6 — это значит найти такие целые неотрицательные числа q и г, что a = bq+r и 0
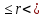6.Теорема. Для любого целого неотрицательного числа а и натурального числа b существуют целые неотрицательные числа q и r, такие, что a = b
q+r, причем
Пара целых неотрицательных чисел (q, г), обладающая этим свойством, единственная.
Свойства множества целых неотрицательных чисел
Множество целых неотрицательных чисел обладает рядом свойств. В частности, оно упорядоченное и бесконечное.
Докажем, что множество целых неотрицательных чисел может быть упорядочено при помощи отношения «меньше». Для этого покажем, что это отношение транзитивно и антисимметрично, причем будем исходить из определения отношения «меньше» через сумму.
Теорема.
Доказательство. Так как
