МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение

высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Высшая школа информационных технологий и автоматизированных систем

^{(наименование высшей школы / филиала / института / колледжа)}
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА

По дисциплине		Web-технологиям
На тему	Разработка веб-приложения – логической игры «Найди пару» по тематике игры God Of War

			Выполнил обучающийся: Филимонов Илья Олегович
			(Ф.И.О.)
			Направление подготовки / специальность: 09.03.03 Прикладная информатика
			(код и наименование)
			Курс: 4 курс
			Группа: 353915
			Руководитель: Пархимович Мария Николаевна, старший
			преподаватель кафедры прикладной информатики и информационной безопасности
			(Ф.И.О. руководителя, должность / уч. степень / звание)
Отметка о зачете
		(отметка прописью)			(дата)
Руководитель					М.Н.Пархимович
		(подпись руководителя)			(инициалы, фамилия)

---

Министерство науки и высшего образования Российской Федерации

федеральное государственное автономное образовательное учреждение

высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Кафедра информационных систем и информационной безопасности

ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ

по

Web-технологиям

студенту

ИТАС

высш. школы

4

курса

353915

группы

Филимонову Илье Олеговичу

09.03.03 Прикладная информатика

ТЕМА:

Разработка веб-приложения – логической игры «Найди пару»

по тематике игры God Of War

ИСХОДНЫЕ ДАННЫЕ:

заполнить

Срок выполнения с

«

19

»

января

2023 г. по

«

04

»

февраля

2023 г.

Руководитель работы

Ст. преподаватель

М.Н. Пархимович

(подпись)

---

Архангельск, 2023
Лист для замечаний

ОГЛАВЛЕНИЕ

1. 
   Постановка задачи
   

1. 
   Описание решения задания
   

Чтобы решить задачу по созданию 3D объекта нужно выполнить следующие действия:

– Создать кривую линию, используя функцию x = 2 + cos(z) с задаваемым количеством точек.

– Произвести вращение линии вокруг оси Z. Количество рёбер должно быть задаваемым.

– Произвести преобразования из мировых в видовые координаты, а потом из видовых в экранные.

– Рассчитать нормаль и среднее Z для каждого полигона.

– Между точек рёбер создать полигоны, чтобы получился трёхмерный объект «Ваза».

– Закрасить полигоны цветом, в зависимости от нормали полигона.

2. 
   Описание координатной модели
   

Для генерации 3D объекта я выбрал формулу x = 2 + cos(z). Функция косинуса – чётная с периодом равным 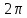. График функции на рисунке 1.


Рисунок 1 – График функции x = 2 + cos(z)

Чтобы сгенерировать трёхмерный объект сначала надо сгенерировать нужное количество точек в пространстве от функции x = 2 + cos(z), а потом сгенерировать рёбра объекта, создавая копии кривой из этих точек, вращая их при этом вокруг оси Z.

В зависимости от необходимого количества рёбер, круг в 360 градусов делится на это количество и получается градус, на который надо отклонить каждое ребро одно от другого.

В своей работе для генерации я использую точки -3,6 и 4,2 на оси Z, что при генерации даёт объект похожий на вазу на рисунке 2.

Число генерируемых точек на кривой задаётся переменной «number_of_points».

---

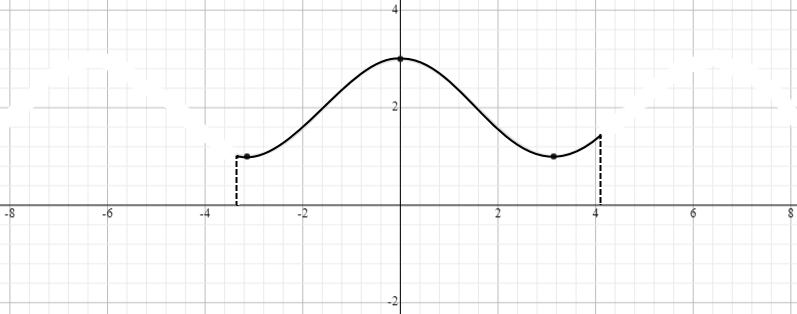
Рисунок 2

3. 
   Описание полигональной модели
   

На рисунке 3 для демонстрации полигональной сетки я приведу вывод программы в режиме отрисовывания линий вместо полигонов.



Рисунок 3 – Вывод программы при отрисовке линиями

Полигональная модель объекта генерируется на основе данных о сгенерированных рёбрах объекта.

Для каждого ребра объекта генерируются полигоны, которые соединяют это ребро с последующим. Последнее ребро соединяется полигонами с начальным ребром.

Дополнительно генерируется полигон дна вазы с нулевыми точками каждого ребра.

Каждое ребро состоит из точек, поэтому каждый полигон ребра объекта соединяет между собой 4 точки против часовой стрелки: начальную ребра номер n, начальную ребра n+1, следующую точку ребра n+1 и следующую точку ребра n. И так далее до конца ребра.



Рисунок 4 – Развёртка полигональной сетки

2. 
   Описание используемых алгоритмов
   

1. 
   Необходимые преобразования координат
   

Рассмотрим способ получения перспективных изображений на основе ана­литической геометрии. Точки в двухмерном и трехмерном пространстве представляются их координатами (X, Y) и (х, у, z) соответственно. При необходимости получе­ния перспективной проекции задается большое количество точек P (x, у, z), принадлежащих объекту, для которых предстоит вы­числить координаты точек изображения Р'(Х, Y) на картинке. Для этого нужно только преобразовать координаты точки Р из так называемых мировых координат (х, у, z) в экранные коорди­наты (X, Y) ее центральной проекции Р'. Будем предполагать, что экран расположен между объектом и глазом Е. Для каждой точки Р объекта прямая линия РЕ пересекает экран в точке Р'.

Это отображение удобно выполнять в два этапа. Первый этап назовем видовым преобразованием - точка Р остается на своем месте, но система мировых координат переходит в систему видовых координат. Второй этап называется перспективным преобразованием. Это точное преобразование точки Р в точку Р' объединенное с переходом из системы трехмерных видовых координат в систему двухмерных экранных координат:

---

Рисунок 5 – Преобразования

2. 
   Видовое преобразование
   

Для выполнения видовых преобразований должны быть зада­ны точка наблюдения и объект. Будет удобно, если начало системы мировых координат располагается вблизи центра объекта, поскольку объект наблюдается в направлении от Е к О на рисунке 2. Пусть точка наблюдения Е будет задана в сферических координатах 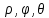по отношению к мировым координатам. То есть мировые координаты (точки Е) могут быть вычислены по формулам: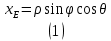







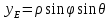
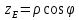
Обозначения сферических координат схематически изображены на рисунке 2.





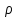
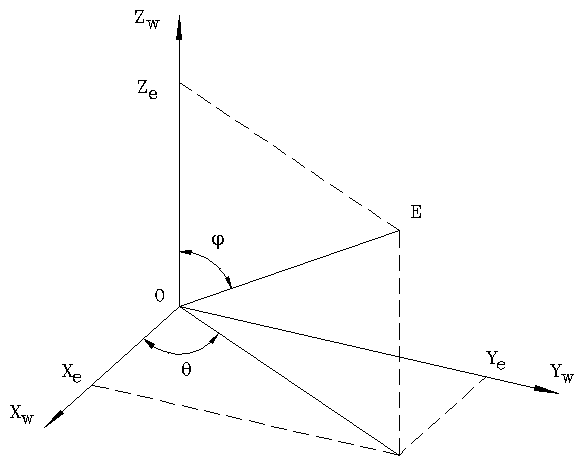
Рисунок 6 - Сферические координаты точки наблюдения Е



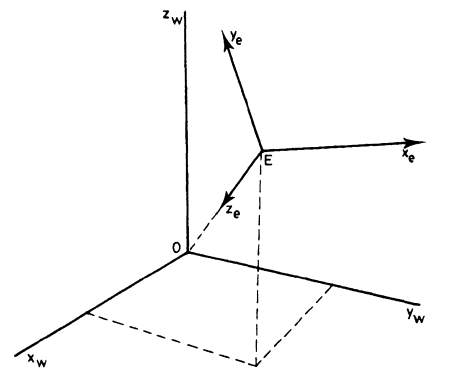
Рисунок 7 - Система видовых координат

Видовое преобразование может быть записано в форме

[х_e y_e z_e 1]=[х_wу_w z_w 1]V (2)

где V - матрица видового преобразования размерами 4х4.

Матрица V, полученная в процессе видового преобразования, выглядит следующим образом:

(3)

3. 
   Перспективное преобразование
   

На рисунке 4 выбрана точка Q, видовые координаты кото­рой равны (0, 0, d) для некоторого положительного числа d. Плоскость z = d определяет экран, который будет использоваться следующим образом. Экран — это плоскость, проходящая через точку Q и перпендикулярная оси z. Экранные координаты определяют­ся привязкой начала к точке Q, а оси Х и Y имеют такие же на­правления, как оси х и у соответственно. Для каждой точки объ­екта Р точка изображения Р' определяется как точка пересече­ния прямой линии

---

Смотрите также файлы

• Общая характеристика Кодекса Юстиниана. 30.doc

• 2ВерноБаллов 1,00 из 1,00Отметить вопросТекст вопросаВ презентацию можно добавить Выберите один ответ a все перечисленное b мультипликацию c звуковые записи d статическую графикуВопрос 3.pdf

• Правовое регулирование бухгалтерского учета за рубежом Титульный лист.docx

• .rtf

• К основным функциям административного права не относят восстановительную.docx