Файл: Разработка вебприложения логической игры Найди пару по тематике игры God Of War.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.04.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РЕ и экрана. Чтобы упростить рисунке 4, будем считать, что точка Р имеет нулевую у-координату. Но все последующие уравнения для вычисления ее у-координаты также пригодны и для любых других значений координаты X. На рисунке 4 треугольники EPR и EP'Q подобны. Следовательно,
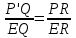 . (4)
. (4)
Отсюда будем иметь
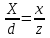 ; (5)
; (5)
X = dx/Z (6)

Рисунок 8 - Экран и видовые координаты
Аналогично можем получить:
Y = dy/Z. (7)
Ранее было введено предположение, что точка О начала системы мировых координат примерно совпадает с центром объекта. Поскольку ось z видовой системы координат совпадает с прямой линией ЕО, которая пересекает экран в точке Q, то начало Q системы экранных координат будет находиться в центре изображения. Если необходимо, чтобы начало координат было смещено относительно центра экрана, то нужно дополнить формулы вычисления X и Yпеременными с1 и с2:
Х = d x/z + с1;
Y = dy/z + c2 (8)
Удаление невидимых линий будет производиться с помощью «алгоритма художника».
Название «алгоритм художника» относится к технике, используемой многими живописцами: сначала рисуются наиболее удалённые части сцены, потом части, которые ближе. Постепенно ближние части начинают перекрывать отдалённые части более удалённых объектов.
Для этого мы вычисляем среднюю координату Z для каждого полигона, сортируем полигоны по этой средней координате, т.е. по удалённости от наблюдателя и выводим полигоны на экран, начиная с более дальнего.
Если предположить, что источник света находится на бесконечности, то лучи света, падающие на поверхность, параллельны между собой. Если к этому добавить условие, что наблюдатель находится в бесконечно удаленной точке, то эффектом ослабления света с увеличением расстояния от источника также можно пренебречь. Кроме того, такое положение наблюдателя означает еще и то, что векторы, направленные от разных точек поверхности к наблюдателю, также будут параллельны. При выполнении всех этих условий плоская грань во всех точках имеет одинаковую интенсивность освещения, поэтому она закрашивается одним цветом. Такое закрашивание называется плоским.
То есть, на каждом полигоне определяется освещенность в произвольной точке, и полученное значение используется для всего полигона. Изображение при этом имеет ярко выраженный полигональный характер – видно, что поверхность состоит из отдельных граней.
При этом, для реализации плоского закрашивания удобно использовать значение нормали к соответствующей грани.
Нахождение нормали по трём точкам.
Пусть заданы три точки (так как через любые три точки можно провести плоскость), например A, B, C. Уравнение плоскости задается в виде:
nx x + ny y + nz z + d=0, (9)
где (nx, ny, nz) – координаты нормали к плоскости.
Получим систему уравнений:
nx x + ny y + nz z + d = 0
nx A.x + ny A.y + nz A.z + d = 0
nx B.x + ny B.y + nz B.z + d = 0 (10)
nx C.x + ny C.y + nz C.z + d = 0
В виде матрицы такая система запишется как:
|| x y z 1 ||
|| A.x A.y A.z 1 ||
|| B.x B.y B.z 1 || = 0 (11)
|| C.x C.y C.z 1 ||
Определитель будет равен (относительно первой строки):
|A.y A.z 1| |A.x A.z 1| |A.x A.y 1| |A.x A.y 1|
x |B.y B.z 1| - y |B.x B.z 1| + z |B.x B.y 1| - |B.x B.y 1| (12)
|C.y C.z 1| |C.x C.z 1| |C.x C.y 1| |C.x C.y 1|
А так как через три точки всегда можно провести плоскость (притом только одну) и число уравнений данной системы равно числу неизвестных, следовательно, система имеет нетривиальное решение (кроме очевидного nx=ny=nz=d=0). Следовательно, определитель данной матрицы равен нулю.
Получаем:
|A.y A.z 1|
nx = |B.y B.z 1|, (13)
|C.y C.z 1|
|A.x A.z 1|
ny = |B.x B.z 1|, (14)
|C.x C.z 1|
|A.x A.y 1|
nz = |B.x B.y 1|. (15)
|C.x C.y 1|
Значение d для определения координат вектора не нужно.
Рассмотрим нахождение значения nx (остальные координаты получаются аналогично):
nx = A.y |B.z 1| - A.z |B.y 1| + |B.y B.z| = (16)
|C.z 1| |C.y 1| |C.y C.z|
= A.y (B.z – C.z) – A.z (B.y – C.y) + (B.y C.z – B.z C.y) =
= A.y (B.z – C.z) + B.y (C.z – A.z) + C.y (A.z – B.z)
Итак, координаты вектора нормали:
nx = A.y (B.z - C.z) + B.y (C.z - A.z) + C.y (A.z - B.z)
ny = A.z (B.x - C.x) + B.z (C.x - A.x) + C.z (A.x - B.x) (17)
nz = A.x (B.y - C.y) + B.x (C.y - A.y) + C.x (A.y - B.y)
Осталось привести вектор к единичной длине, так как для определения косинуса угла между векторами проще использовать единичные векторы. Для этого нужно определить длину вектора и разделить на нее каждую координату.
Для каждой грани при инициализации объекта нужно посчитать вектор нормали, привести к единичной длине и сохранить его координаты в структуре соответствующей грани. Кроме того, при каждом повороте сцены векторы нормали нужно тоже пересчитывать (но перспективную проекцию находить не следует).
Использование нормали к грани для определения освещенности.
Кроме номеров точек треугольника в структуре, задающей полигон, определен его цвет. И в зависимости от угла между направлением взгляда и нормалью этот цвет должен изменяться. С одной стороны, значение координаты nz нормали для видимой грани изменяется в диапазоне [-1, 0), с другой – цвет грани задан в виде RGB компонентов. Поэтому для получения цвета грани нужно умножить каждую компоненту на абсолютное значение nz.
Для вращения вокруг оси Z на угол α воспользуемся матрицей поворота в трёхмерном пространстве:
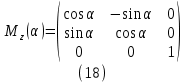
То есть для наших координат x, y, z это будет формула:

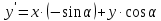

Основные переменные представлены в таблице 1.
Таблица 1 – Основные переменные
В качестве отображения визуальной информации я использую библиотеку tkinter и её класс Canvas.
Для работы с начальной генерируемой кривой я сделал класс «Curve». Внутри него в его переменной «points_array» будут храниться мировые координаты генерируемой кривой. При создании экземпляра класса необходим предоставить z0, zn, number_of_points.
z0 – начальная координата z,
zn – конечная координата z,
number_of_points – количество генерируемых точек.
Для вращения этой кривой в этом классе предусмотрена функция «transform_rotate», которая возвращает экземпляр класса «Vase». На вход функции параметром number_of_edges задаётся количество необходимых рёбер.
Потом мы вызываем функцию «view_transformation», чтобы получить две матрицы: матрицу с видовыми координатами (v_matrix) и матрицу с экранными координатами (d_matrix).
Потом мы генерируем объект в памяти класса Image из библиотеки Pillow, чтобы произвести там отрисовку, которую потом можно будет скопировать в поле Canvas.
Потом мы вызываем функцию «draw_object», чтобы нарисовать наш трёхмерный объект на экземпляре класса Image. При его создании мы передаём матрицу с видовыми координатами (v_matrix), матрицу с экранными координатами (d_matrix) и указатель на экземпляр класса «image1».
В функции «draw_object» мы обходим все рёбра объекта и создаём массив координат полигонов, их нормалей и среднее значение координаты z, используя вспомогательный класс «PolygonsMatrix».
После обработки всех рёбер добавляем один дополнительный полигон для дна «Вазы».
Потом проводим сортировку полигонов в зависимости от средней координаты z.
И потом рисуем все полигоны на экземпляре класса Image, раскрашивание полигона происходит в зависимости от нормали к полигону.
После выхода из функции «draw_object» мы удаляем всё с полотна (Canvas) и добавляем на него уже отрисованный рисунок из экземпляра класса Image.
В результате, в нашем окне программы появляется нарисованный трёхмерный объект.
Для изменения ракурса предусмотрены кнопки управления «Влево», «Вправо», «Вверх», «Вниз». Так же можно управлять с помощью стрелок клавиатуры.
В данной части должно быть описание интерфейса; руководство по использованию программы; примеры получаемых изображений.
После запуска программы можно увидеть поле, на котором отрисовывается объект «Ваза» и кнопки управления.

Рисунок 9
Для изменения ракурса предусмотрены кнопки управления «Влево», «Вправо», «Вверх», «Вниз». Так же можно управлять с помощью стрелок клавиатуры.
С помощью клавиш «Вверх» и «Вниз» меняется точка осмотра объекта в трёхмерном пространстве вверх или вниз.

Рисунок 10
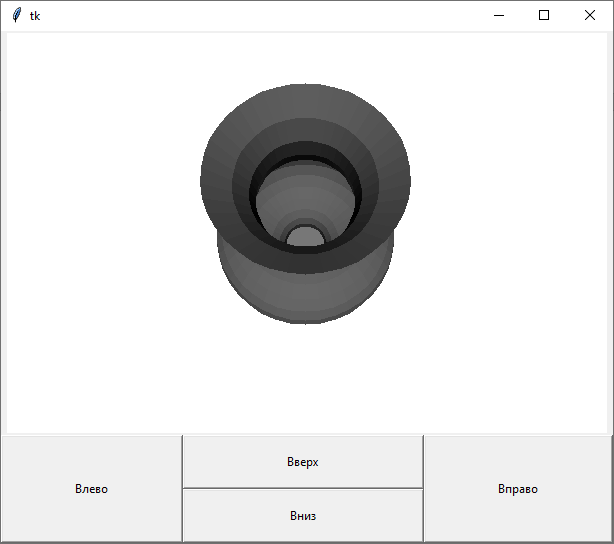
Рисунок 11
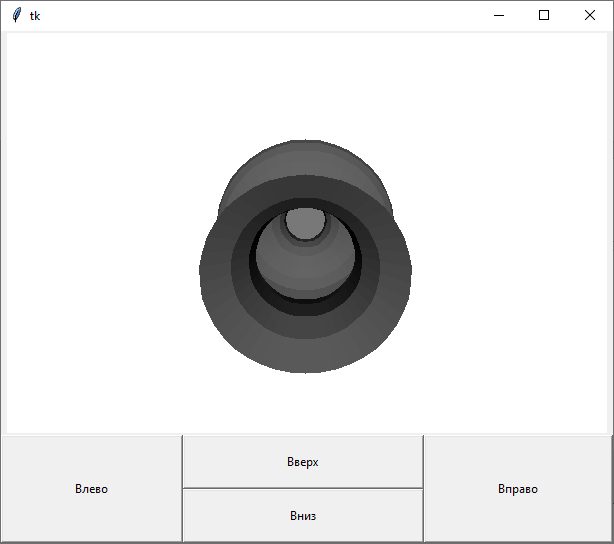
Рисунок 12

Рисунок 13
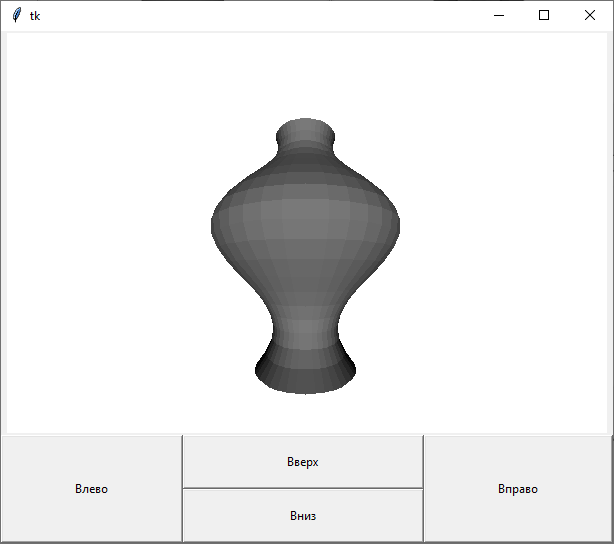
Рисунок 14
С помощью клавиш «Вправо» и «Влево» меняется точка осмотра объекта в трёхмерном пространстве вправо или влево.
Если поменять параметры «number_of_points» и «number_of_edges», то получим вариант объекта с другим количеством рёбер и точек на исходной линии.
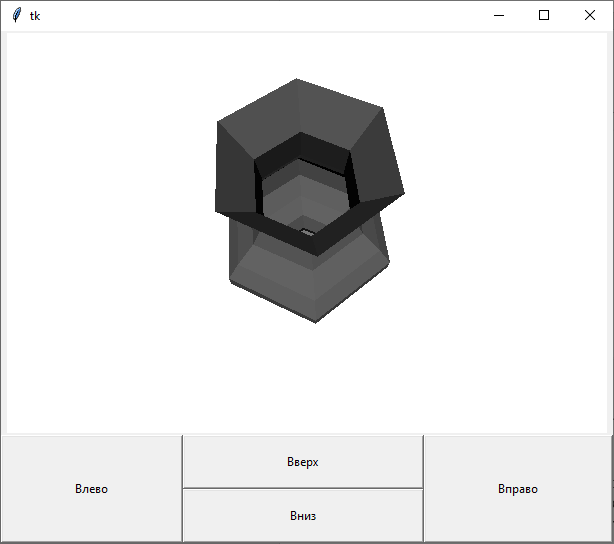
Рисунок 15
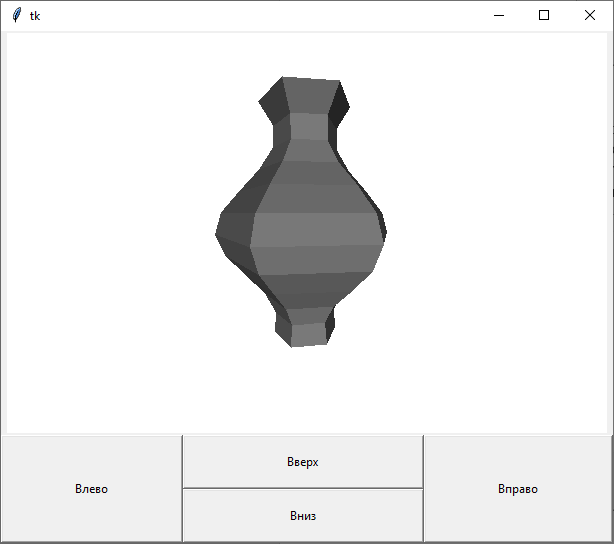
Рисунок 16
Заключение
Используя библиотеку tkinter для вывода графической информации, я выполнил расчётно-графическую работу на тему «Создание тел вращения».
Для вращения выбрана функция x = 2 + cos(z). Вращение происходит вокруг оси Z.
Реализованы функции для генерации исходной кривой с задаваемым количеством точек.
Реализовано добавление рёбер путём вращения вокруг оси Z с задаваемым количеством рёбер.
Реализовано преобразование из мировых в видовые координаты, а потом из видовых в экранные.
Удаление невидимых граней выполнено с использованием «алгоритма художника».
Закрашивание полигонов выполнено с использованием модели плоского закрашивания.
Список использованных источников
Приложение. Листинг приложения
import tkinter as tk
from math import sin, cos, pi, sqrt
from PIL import Image, ImageDraw, ImageTk
import numpy as np
################################################
# глобальные переменные #
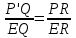 . (4)
. (4)Отсюда будем иметь
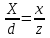 ; (5)
; (5)X = dx/Z (6)

Рисунок 8 - Экран и видовые координаты
Аналогично можем получить:
Y = dy/Z. (7)
Ранее было введено предположение, что точка О начала системы мировых координат примерно совпадает с центром объекта. Поскольку ось z видовой системы координат совпадает с прямой линией ЕО, которая пересекает экран в точке Q, то начало Q системы экранных координат будет находиться в центре изображения. Если необходимо, чтобы начало координат было смещено относительно центра экрана, то нужно дополнить формулы вычисления X и Yпеременными с1 и с2:
Х = d x/z + с1;
Y = dy/z + c2 (8)
-
Удаление невидимых линий
Удаление невидимых линий будет производиться с помощью «алгоритма художника».
Название «алгоритм художника» относится к технике, используемой многими живописцами: сначала рисуются наиболее удалённые части сцены, потом части, которые ближе. Постепенно ближние части начинают перекрывать отдалённые части более удалённых объектов.
Для этого мы вычисляем среднюю координату Z для каждого полигона, сортируем полигоны по этой средней координате, т.е. по удалённости от наблюдателя и выводим полигоны на экран, начиная с более дальнего.
-
Модель плоского закрашивания
Если предположить, что источник света находится на бесконечности, то лучи света, падающие на поверхность, параллельны между собой. Если к этому добавить условие, что наблюдатель находится в бесконечно удаленной точке, то эффектом ослабления света с увеличением расстояния от источника также можно пренебречь. Кроме того, такое положение наблюдателя означает еще и то, что векторы, направленные от разных точек поверхности к наблюдателю, также будут параллельны. При выполнении всех этих условий плоская грань во всех точках имеет одинаковую интенсивность освещения, поэтому она закрашивается одним цветом. Такое закрашивание называется плоским.
То есть, на каждом полигоне определяется освещенность в произвольной точке, и полученное значение используется для всего полигона. Изображение при этом имеет ярко выраженный полигональный характер – видно, что поверхность состоит из отдельных граней.
При этом, для реализации плоского закрашивания удобно использовать значение нормали к соответствующей грани.
Нахождение нормали по трём точкам.
Пусть заданы три точки (так как через любые три точки можно провести плоскость), например A, B, C. Уравнение плоскости задается в виде:
nx x + ny y + nz z + d=0, (9)
где (nx, ny, nz) – координаты нормали к плоскости.
Получим систему уравнений:
nx x + ny y + nz z + d = 0
nx A.x + ny A.y + nz A.z + d = 0
nx B.x + ny B.y + nz B.z + d = 0 (10)
nx C.x + ny C.y + nz C.z + d = 0
В виде матрицы такая система запишется как:
|| x y z 1 ||
|| A.x A.y A.z 1 ||
|| B.x B.y B.z 1 || = 0 (11)
|| C.x C.y C.z 1 ||
Определитель будет равен (относительно первой строки):
|A.y A.z 1| |A.x A.z 1| |A.x A.y 1| |A.x A.y 1|
x |B.y B.z 1| - y |B.x B.z 1| + z |B.x B.y 1| - |B.x B.y 1| (12)
|C.y C.z 1| |C.x C.z 1| |C.x C.y 1| |C.x C.y 1|
А так как через три точки всегда можно провести плоскость (притом только одну) и число уравнений данной системы равно числу неизвестных, следовательно, система имеет нетривиальное решение (кроме очевидного nx=ny=nz=d=0). Следовательно, определитель данной матрицы равен нулю.
Получаем:
|A.y A.z 1|
nx = |B.y B.z 1|, (13)
|C.y C.z 1|
|A.x A.z 1|
ny = |B.x B.z 1|, (14)
|C.x C.z 1|
|A.x A.y 1|
nz = |B.x B.y 1|. (15)
|C.x C.y 1|
Значение d для определения координат вектора не нужно.
Рассмотрим нахождение значения nx (остальные координаты получаются аналогично):
nx = A.y |B.z 1| - A.z |B.y 1| + |B.y B.z| = (16)
|C.z 1| |C.y 1| |C.y C.z|
= A.y (B.z – C.z) – A.z (B.y – C.y) + (B.y C.z – B.z C.y) =
= A.y (B.z – C.z) + B.y (C.z – A.z) + C.y (A.z – B.z)
Итак, координаты вектора нормали:
nx = A.y (B.z - C.z) + B.y (C.z - A.z) + C.y (A.z - B.z)
ny = A.z (B.x - C.x) + B.z (C.x - A.x) + C.z (A.x - B.x) (17)
nz = A.x (B.y - C.y) + B.x (C.y - A.y) + C.x (A.y - B.y)
Осталось привести вектор к единичной длине, так как для определения косинуса угла между векторами проще использовать единичные векторы. Для этого нужно определить длину вектора и разделить на нее каждую координату.
Для каждой грани при инициализации объекта нужно посчитать вектор нормали, привести к единичной длине и сохранить его координаты в структуре соответствующей грани. Кроме того, при каждом повороте сцены векторы нормали нужно тоже пересчитывать (но перспективную проекцию находить не следует).
Использование нормали к грани для определения освещенности.
Кроме номеров точек треугольника в структуре, задающей полигон, определен его цвет. И в зависимости от угла между направлением взгляда и нормалью этот цвет должен изменяться. С одной стороны, значение координаты nz нормали для видимой грани изменяется в диапазоне [-1, 0), с другой – цвет грани задан в виде RGB компонентов. Поэтому для получения цвета грани нужно умножить каждую компоненту на абсолютное значение nz.
-
Вращение вокруг оси Z
Для вращения вокруг оси Z на угол α воспользуемся матрицей поворота в трёхмерном пространстве:
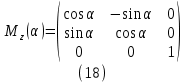
То есть для наших координат x, y, z это будет формула:

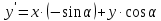

-
Описание программы
-
Описание переменных
Основные переменные представлены в таблице 1.
Таблица 1 – Основные переменные
| Переменная | Предназначение |
| ro, teta, phi | Сферические координаты точки наблюдения |
| window_width | Ширина холста (Canvas), на котором мы будем отображать наш объект |
| window_height | Высота холста (Canvas), на котором мы будем отображать наш объект |
| d | Расстояние от точки наблюдения до экрана |
| c | Экземпляр класса Canvas для отображения на экране |
| number_of_points | Количество точек аппроксимации исходной кривой |
| number_of_edges | Количество рёбер генерируемого объекта |
-
Описание работы программы
В качестве отображения визуальной информации я использую библиотеку tkinter и её класс Canvas.
Для работы с начальной генерируемой кривой я сделал класс «Curve». Внутри него в его переменной «points_array» будут храниться мировые координаты генерируемой кривой. При создании экземпляра класса необходим предоставить z0, zn, number_of_points.
z0 – начальная координата z,
zn – конечная координата z,
number_of_points – количество генерируемых точек.
Для вращения этой кривой в этом классе предусмотрена функция «transform_rotate», которая возвращает экземпляр класса «Vase». На вход функции параметром number_of_edges задаётся количество необходимых рёбер.
Потом мы вызываем функцию «view_transformation», чтобы получить две матрицы: матрицу с видовыми координатами (v_matrix) и матрицу с экранными координатами (d_matrix).
Потом мы генерируем объект в памяти класса Image из библиотеки Pillow, чтобы произвести там отрисовку, которую потом можно будет скопировать в поле Canvas.
Потом мы вызываем функцию «draw_object», чтобы нарисовать наш трёхмерный объект на экземпляре класса Image. При его создании мы передаём матрицу с видовыми координатами (v_matrix), матрицу с экранными координатами (d_matrix) и указатель на экземпляр класса «image1».
В функции «draw_object» мы обходим все рёбра объекта и создаём массив координат полигонов, их нормалей и среднее значение координаты z, используя вспомогательный класс «PolygonsMatrix».
После обработки всех рёбер добавляем один дополнительный полигон для дна «Вазы».
Потом проводим сортировку полигонов в зависимости от средней координаты z.
И потом рисуем все полигоны на экземпляре класса Image, раскрашивание полигона происходит в зависимости от нормали к полигону.
После выхода из функции «draw_object» мы удаляем всё с полотна (Canvas) и добавляем на него уже отрисованный рисунок из экземпляра класса Image.
В результате, в нашем окне программы появляется нарисованный трёхмерный объект.
Для изменения ракурса предусмотрены кнопки управления «Влево», «Вправо», «Вверх», «Вниз». Так же можно управлять с помощью стрелок клавиатуры.
-
Тестирование программы
В данной части должно быть описание интерфейса; руководство по использованию программы; примеры получаемых изображений.
После запуска программы можно увидеть поле, на котором отрисовывается объект «Ваза» и кнопки управления.

Рисунок 9
Для изменения ракурса предусмотрены кнопки управления «Влево», «Вправо», «Вверх», «Вниз». Так же можно управлять с помощью стрелок клавиатуры.
С помощью клавиш «Вверх» и «Вниз» меняется точка осмотра объекта в трёхмерном пространстве вверх или вниз.

Рисунок 10

Рисунок 11

Рисунок 12

Рисунок 13

Рисунок 14
С помощью клавиш «Вправо» и «Влево» меняется точка осмотра объекта в трёхмерном пространстве вправо или влево.
Если поменять параметры «number_of_points» и «number_of_edges», то получим вариант объекта с другим количеством рёбер и точек на исходной линии.

Рисунок 15

Рисунок 16
Заключение
Используя библиотеку tkinter для вывода графической информации, я выполнил расчётно-графическую работу на тему «Создание тел вращения».
Для вращения выбрана функция x = 2 + cos(z). Вращение происходит вокруг оси Z.
Реализованы функции для генерации исходной кривой с задаваемым количеством точек.
Реализовано добавление рёбер путём вращения вокруг оси Z с задаваемым количеством рёбер.
Реализовано преобразование из мировых в видовые координаты, а потом из видовых в экранные.
Удаление невидимых граней выполнено с использованием «алгоритма художника».
Закрашивание полигонов выполнено с использованием модели плоского закрашивания.
Список использованных источников
-
Аммерал, Л. Принципы программирования в машинной графике. Пер. с англ. — М. [Текст]: "Сол Систем", 1992. — 224 с. -
NumPy v1.20 Manual [Electronic resource]. – Electronic text data. – Mode of access : https://numpy.org/doc/stable/, free access (24.05.2021). – Title from screen. -
Pillow Handbook [Electronic resource]. – Electronic text data. – Mode of access : https://pillow.readthedocs.io/en/stable/handbook/index.html, free access (24.05.2021). – Title from screen. -
Python 3.9.5 documentation [Electronic resource]. – Electronic text data. – Mode of access : https://docs.python.org/3/, free access (24.05.2021). – Title from screen. -
Tkinter – Python interface to Tcl/Tk [Electronic resource]. – Electronic text data. – Mode of access : https://docs.python.org/3/library/tkinter.html, free access (24.05.2021). – Title from screen.
Приложение. Листинг приложения
import tkinter as tk
from math import sin, cos, pi, sqrt
from PIL import Image, ImageDraw, ImageTk
import numpy as np
################################################
# глобальные переменные #

