1. 
   Действительное число (вещественное число), любое положительное число, отрицательное число или нуль. Погре́шность измере́ния — отклонение измеренного значения величины от её истинного (действительного) значения.
   
2. 
   Делимость – это способность одного числа делиться на другое без остатка или нацело. При́знак дели́мости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному. 
   
3. 
   Формулы сокращённого умножения
   

формула квадрата суммы: (a+b)2=a2+2ab+b2a+b2=a2+2ab+b2

квадратная формула разности: (a−b)2=a2−2ab+b2a-b2=a2-2ab+b2

формула куба суммы: (a+b)3=a3+3a2b+3ab2+b3a+b3=a3+3a2b+3ab2+b3

формула куба разности: (a−b)3=a3−3a2b+3ab2−b3a-b3=a3-3a2b+3ab2-b3

формула разности квадратов: a2−b2=(a−b)(a+b)a2-b2=a-ba+b

формула суммы кубов: a3+b3=(a+b)(a2−ab+b2)a3+b3=a+ba2-ab+b2

4. 
   Уравнением называется равенство двух выражений, в которых есть буквенная переменная. Линейное уравнение — это алгебраическое уравнение, у которого полная степень составляющих его многочленов равна 1. Квадратным уравнением называют уравнение второй степени и определяют. Уравнением с модулем называют равенство, содержащее переменную под знаком модуля. Рациональное уравнение — это такой вид уравнения в которой левая и правая части рациональные выражения.
   
5. 
   Систе́ма уравне́ний — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
   
6. 
   Линейными называются неравенства левая и правая часть которых представляет собой линейные функции относительно неизвестной величины. Квадратными неравенствами называют неравенства, которые можно привести к виду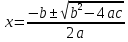 . Неравенства с модулем представляют собой такие неравенства, в которых неизвестные находятся под знаком модуля. Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств. Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция.
   

7. 
   Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство. Совокупность неравенств – это запись, представляющая собой несколько записанных одно под другим неравенств, объединенных слева квадратной скобкой, и обозначающая множество решений, являющихся решениями хотя бы одного из неравенств совокупности
   

---

8. 
   Степень – Произведение n множителей, каждый из которых равен а
   

Свойства степеней:

1. 
   Любое число в первой степени равно самому себе
   
2. 
   Любое число в нулевой степени равно
   
3. 
    Единица в любой степени равна
   
4. 
   При умножении степеней с одинаковыми основаниями показатели складываются
   
5. 
   При делении степеней с одинаковыми основаниями показатели вычитаются
   
6. 
   При возведении степени в степень показатели умножаются
   
7. 
   При возведении произведения в степень каждый множитель возводится в эту степень: (ab)ⁿ = aⁿbⁿ
   
8. 
   Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень
   
9. 
   Степень с дробным показателем можно представить в виде корня некоторой степени по формуле 
   
10. 
    Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса
    

9. 
   Степенная функция – это функция вида f (x) = x a, где: a – показатель степени, является действительным числом, a ≠ 0; x – основание степени, это свободная переменная. Степенной функцией называют такую функцию, которая имеет вид: y = x a. Где a является показателем степени и действительным числом. Где a является показателем степени и действительным числом.
   
10. 
    Иррациональным уравнением называется уравнение, в котором переменная содержится под знаком корня или под знаком операции возведения в дробную степень. Иррациональными называют неравенства, в которых переменные входят  под знаком корня.
    
11. 
    Показательная функция – это функция вида f (x) = a x, где: a– основание степени, при этом a > 0 и a ≠ 1; x– показатель степени. Показательная функция обладает следующими свойствами: D (f): множество R всех действительных чисел; E (f): множество всех положительных чисел; f (x)>0 при любом значении х; 
    
12. 
    Показательное уравнение — это уравнение, в котором неизвестная величина находится в показателе степени. Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании. Методы решения уравнений:
    

• 
  метод приведения к одному основанию;
  
• 
  метод введения новых переменных;
  
• 
  метод вынесения общего множителя за скобки;
  
• 
  метод почленного деления;
  
• 
  метод группировки;
  
• 
  метод оценки.
  

---

Методы решения неравенств:

1) переход от неравенства между 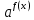  и 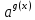 к равносильному неравенству между f(x) и g(x), где знаки определяются значением a (см. определение выше);
2) графический метод;
3) замена переменной.

13. 
    Логарифм – положительная числа b по основанию a причем a больше нуля и не равно единицы называют показателем степени . Основное логарифмическое тождество — это способ превращения четырехэтажного выражения в простейшую b.
    
14. 
    Логарифмическая функция – это такая функция, которая записана в виде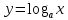 Основные свойства логарифмической функции:
    

1. область определения; + ∞; 2. множество значений− ∞; + ∞; 3. если a>1, то функция возрастает на всей области определения; если 0

15. 
    Логарифмическое уравнение - это уравнение, в котором неизвестное находится под знаком логарифма. Логарифмическим неравенством называется такое неравенство, в котором неизвестная величина содержится или под знаком логарифма, или в его основании. (Название методов не нашел :D)
    
16. 
    Аксиомы стереометрии:
    

1. Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость

2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей

Следствия из аксиом стереометрии:

Теорема 1. Через прямую и не лежащую на ней точку проходит единственная плоскость

Теорема 2. Через две пересекающиеся прямые проходит единственная плоскость

Теорема 3. Через две параллельные прямые проходит единственная плоскость

17. 
    Возможны четыре различных случая расположения двух прямых в пространстве:
    

прямые скрещиваются, т. е. не лежат в одной плоскости

прямые пересекаются, т. е. лежат в одной плоскости и имеют одну общую точку

прямые параллельны, т. е. лежат в одной плоскости и не пересекаются

прямые совпадают

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

18. 
    Существуют три случая взаимного расположения прямой и плоскости в пространстве:
    

прямая лежит (находится) в плоскости

прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются)

прямая и плоскость не имеют ни одной общей точки

Прямая и плоскость параллельны, если они не имеют общих точек.

19. 
    Если две плоскости имеют общую точку, то они пересекаются прямой, если две плоскости не имеют общих точек, то они параллельны друг другу.
    
20. 
    Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Теорема о трех перпендикулярах – если прямая, проведенная на плоскости через основание наклонной, перпендикулярна самой наклонной, то она перпендикулярна и её проекции
    
21. 
    Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
    

Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

22. 
    Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей.
    

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

1.Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

2.Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.

3.Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.

4.Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения

23. 
    Многогранник — это тело, ограниченное конечным числом плоскостей. При́зма — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её основаниями.
    

Правильная призма — это прямая призма, основанием которой является правильный многоугольник.

24. 
    Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм.
    

Свойства параллелепипеда:

противоположные грани параллелепипеда равны и параллельны

Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам

Боковые грани прямого параллелепипеда — прямоугольники

25. 
    Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. Усечённая пирамида — часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию.
    

Параллельное сечение пирамиды обладает следующими свойствами:

1.сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых рёбрах пропорциональные отрезки

2.в сечении получается многоугольник, подобный основанию

3.площади сечения и основания относятся как квадраты их расстояний до вершины

26. 
    Многогранник — это тело, ограниченное конечным числом плоскостей.
    

Правильный многогранник – выпуклый многогранник, все грани которого равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

---

Смотрите также файлы

• Разработка программы Таблица умножения.docx

• Разметка страницы.docx

• Обведите ту кнопку, на которой необходимо щелкнуть, чтобы увеличить окно программы.doc

• Осы сабата ол жеткізілетін оу масаттары (оу бадарламасына сілтеме).docx

• Тема 1.docx