Файл: Решение. По рисунку определяем координаты векторов и . Найдём разность векторов и.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 16
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
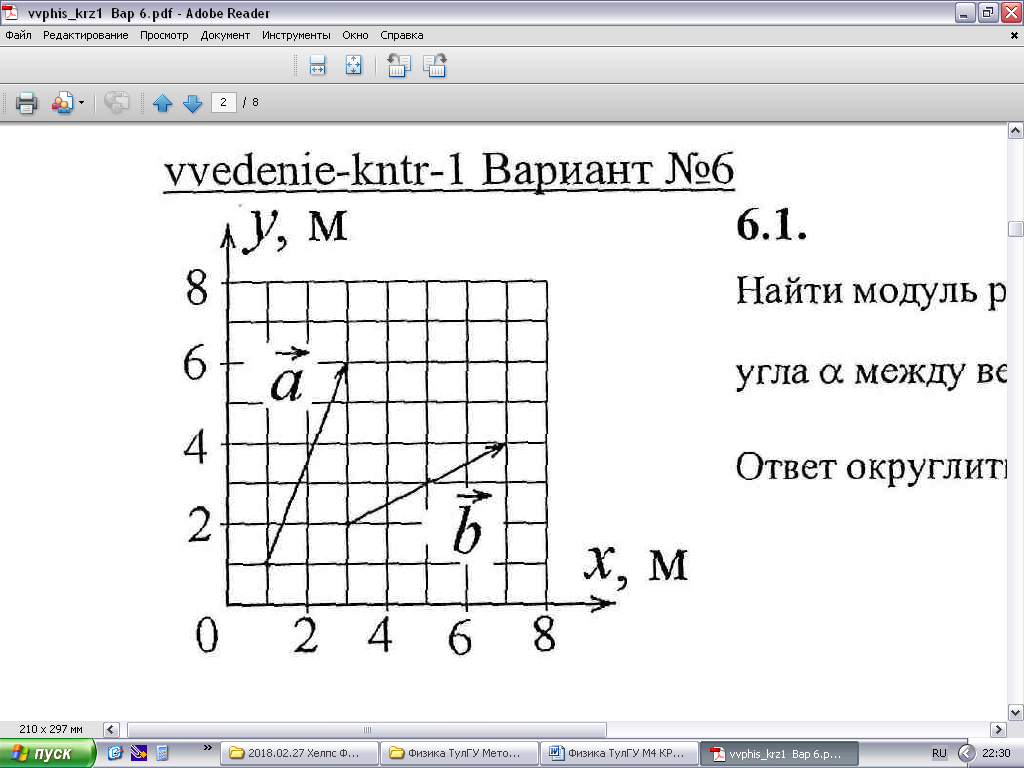
6.1. Найти модуль разности векторов |a – b| и косинус угла между векторами a и b.
Ответ округлить до двух значащих цифр.
Решение.
По рисунку определяем координаты векторов
и 
:
, 
.Найдём разность векторов
и :
.Вычислим модуль разности векторов
и :
.Найдём скалярное произведение векторов
и :
.Найдём модули векторов
и :
;
.Вычислим косинус угла
между векторами
и 
:
.Ответ:
, 
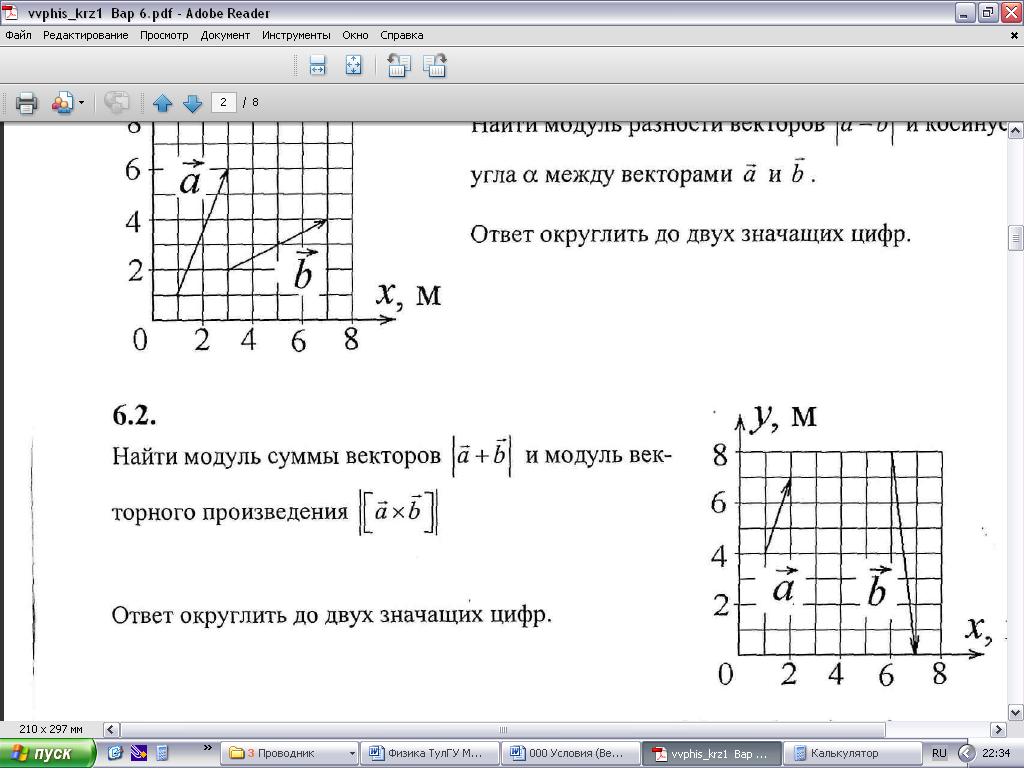
.6.2. Найти модуль суммы векторов |a + b| и модуль векторного произведения |[axb]|.
Ответ округлить до двух значащих цифр.
Решение.
По рисунку определяем координаты векторов
и :
, 
.Найдём сумму векторов
и :
.Вычислим модуль суммы векторов
и :
.Найдём модуль векторного произведения векторов
и :
.
Ответ:
, 
.6.3. Найти значение производной от функции
f(x) = sin(cosx) + 4x5
в точке с координатой x = 1.
Решение.
Найдём производную заданной функции, используя правила дифференцирования и таблицу производных:
;
;
;
.Вычислим значение производной в точке
:
.Ответ:
.6.4. Найти частные производные z`x и z`y функции
z = ln(x2 + y).
Решение.
Частную производную по
найдём, считая переменную 
постоянной:
Частную производную по
найдём, считая переменную постоянной:
Ответ:
,
.6.5. Найти градиент функции u = f(x,y,z) в точке M.
u = ln(3 – x2) + xy2z, M(1; 3; 2).
Решение.
Вектор-градиент скалярного поля u = f(x,y,z) равен:
.Найдём значения частных производных функции в точке M:
,
;
,
;
,
.Запишем градиент скалярного поля u в точке М:
.Ответ:
.