29. Интервальные оценки математического ожидания и дисперсии.

Рассматривается выборка  некоторой генеральной случайной величины. Поставим задачу нахождения интервала, покрывающего величину  с заданной вероятностью, близкой к единице. Требуется определить статистики (границы интервала)





такие, что интервал  накрывает величину  с вероятностью 



Интервал  называется интервальной оценкой, или доверительным интервалом.
Интервальные оценки математического ожидания при неизвестной дисперсии

Генеральная случайная величина Х распределена нормально с неизвестным математическим ожиданием и неизвестной дисперсией  Эффективной оценкой для параметра аявляется оценка  а эффективной оценкой для дисперсии является  Статистика  имеет распределение Стьюдента с  степенью свободы. Распределение этой статистики не зависит от параметроваи 

---

Случайную величину, имеющую распределение Стьюдента с kстепенями свободы, принято обозначать  В таблице 2 даны значения  соответствующие вероятности  Задавая число степеней свободыkи вероятностьр, находим значение  По  и  при помощи таблицы 2 определяем значение 



И так как распределение статистики  совпадает с распределением  то имеем:



Решаем неравенство  относительноа, получаем:

При этом  ошибка оценки параметрааравна  Таким образом,с вероятностью   доверительный интервал   покрывает величинуа.
5.2.3 Интервальные оценки дисперсии (среднеквадратического отклонения) при известном математическом ожидании
Рассматривается случайная выборка 

---

генеральной случайной величиныХ, нормально распределенной с известным математическим ожиданиемаи неизвестной дисперсией  Эффективной оценкой дисперсии является  Статистика  распределена по закону  спстепенями свободы. Распределение  от величины  не зависит.

Случайную величину, распределенную по закону  сkстепенями свободы, принято обозначать  В таблице 3 указаны значения  соответствующие вероятности  Задаваяри число степеней свободыk, определяем  Из таблицы 3 по  и  находим  по  и  находим  Так как статистика 

---

распределена по закону  то



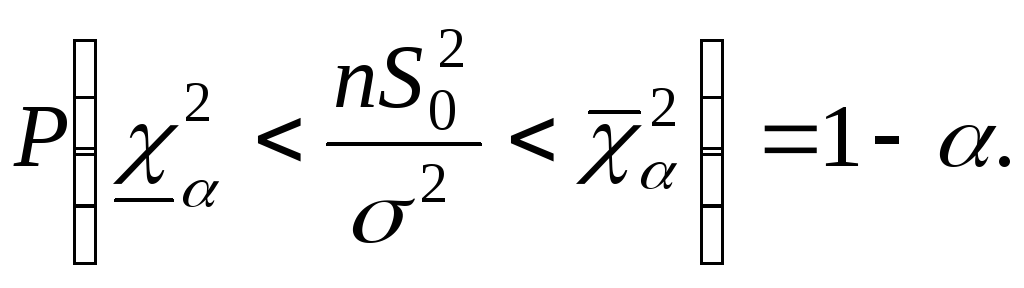
Решаем неравенство  относительно  получаем:


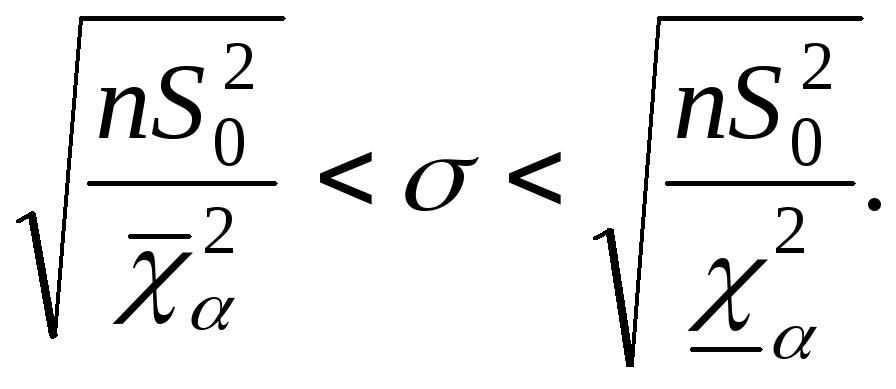Итак, с доверительной вероятностью   доверительный интервал  покрывает величину 

В данном случае доверительный интервал не симметричен относительно оценки 

Интервальные оценки дисперсии (среднеквдратического отклонения) при неизвестном математическом ожидании
Рассматривается случайная выборка  генеральной случайной величиныХ, нормально распределенной с неизвестными параметрамиаи  Наилучшей оценкой дисперсии является  Распределение статистики  совпадает с распределением  Используем таблицу 3: по  и  находим по и

---

находим  С вероятностью  выполняется неравенство:



Разрешим это неравенство относительно 

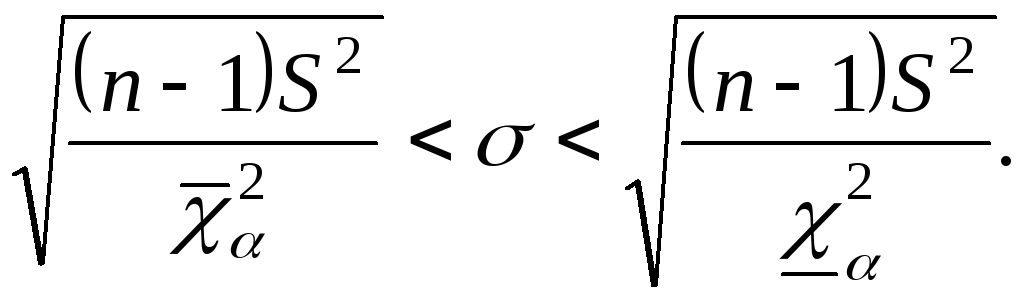С доверительной вероятностью 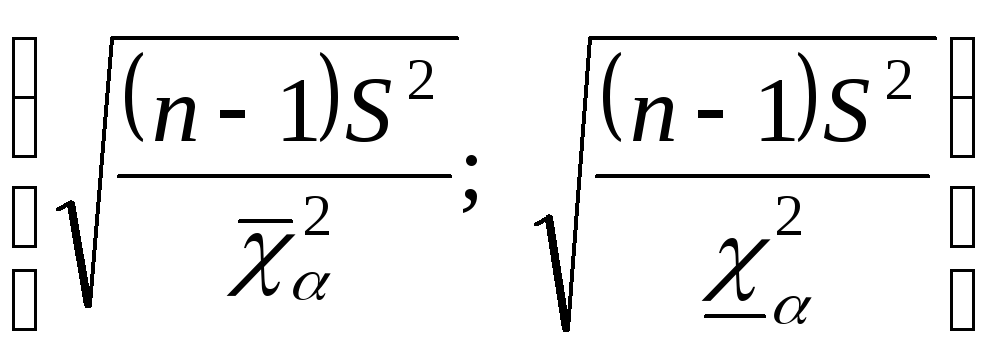  доверительный интервал   покрывает параметр 

---

Смотрите также файлы

• Лекция 01. Основные принципы построения распределенных информационных систем Скворцов С. Е. 15 января 2019.docx

• Изучение точных теодолитов.docx

• Самостоятельная работа по теме Однородные члены предложения. Знаки препинания при однородных членах.docx

• Титульный лист центросоюз рф.docx

• Контрольная работа по дисциплине Финансовые механизмы и инструменты в государственном и муниципальном управлении Тема вопросы 10,11 Институт непрерывного и дистанционного образования Направление подготовки.docx