Лингвистическая переменная (ЛП) – это переменная, значение которой определяется набором вербальных (то есть словесных) характеристик некоторого свойства.

Например, ЛП «рост» определяется через набор {карликовый, низкий, средний, высокий, очень высокий}.

Введя понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, был предложен аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений. Это позволило создать фундамент теории нечетких множеств и нечеткой логики, а также предпосылки для внедрения методов нечеткого управления в инженерную практику.

Основы теории нечетких множеств

Значения лингвистической переменной (ЛП) определяются через так называемые нечеткие множества (НМ), которые в свою очередь определены на некотором базовом наборе значений или базовой числовой шкале, имеющей размерность. Каждое значение ЛП определяется как нечеткое множество (например, НМ «низкий рост»).

Нечеткое множество определяется через некоторую базовую шкалу В и функцию принадлежности НМ – µ(х), х 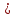В, принимающую значения на интервале [0...1]. Таким образом, нечеткое множество В – это совокупность пар вида (х, µ(х)), где х 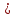В. Часто встречается и такая запись:
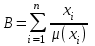(6.1)
где х – i-e значение базовой шкалы.

Функция принадлежности определяет субъективную степень уверенности эксперта в том, что данное конкретное значение базовой шкалы соответствует определяемому НМ. Эту функцию не стоит путать с вероятностью, носящей объективный характер и подчиняющейся другим математическим зависимостям. Например, для двух экспертов определение НМ «высокая» для ЛП «цена автомобиля» в условных единицах может существенно отличаться в зависимости от их социального и финансового положения.

«Высокая_цена_автомобиля_1» = {50000/1 + 25000/0.8 + 10000/0.6 + 5000/0.4}; «Высокая_цена_автомобиля_2» = {25000/1 + 10000/0.8 + 5000/0.7 + 3000/0.4}.

Пример.6.1

Пусть перед нами стоит задача интерпретации значений ЛП «возраст», таких как «молодой» возраст, «преклонный» возраст или «переходный» возраст. Определим «возраст» как ЛП (рис.6.1.). Тогда «молодой», «преклонный», «переходный» будут значениями этой лингвистической переменной. Более полно базовый набор значений ЛП «возраст» следующий:

---

В – {младенческий, детский, юный, молодой, зрелый, преклонный, старческий}.

Для ЛП «возраст» базовая шкала – это числовая шкала от 0 до 120, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории возраста (от 0 до 1). На рис.6.2 отражено, как одни и те же значения базовой шкалы могут участвовать в определении различных НМ.



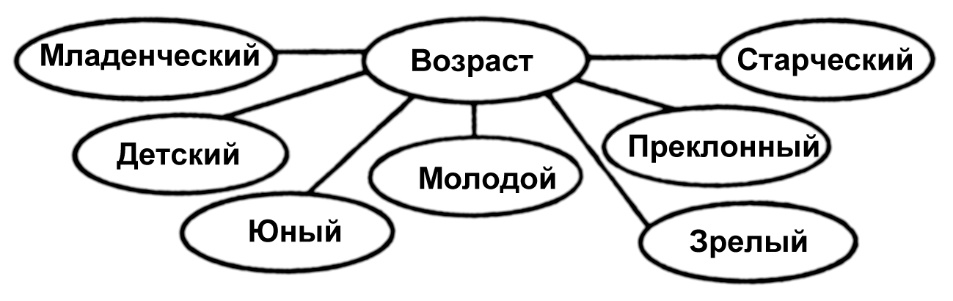
Рис. 6.1. Лингвистическая переменная «возраст» и нечеткие множества, определяющие ее значения
Например, определить значение НМ «младенческий возраст» можно так:




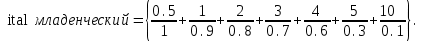
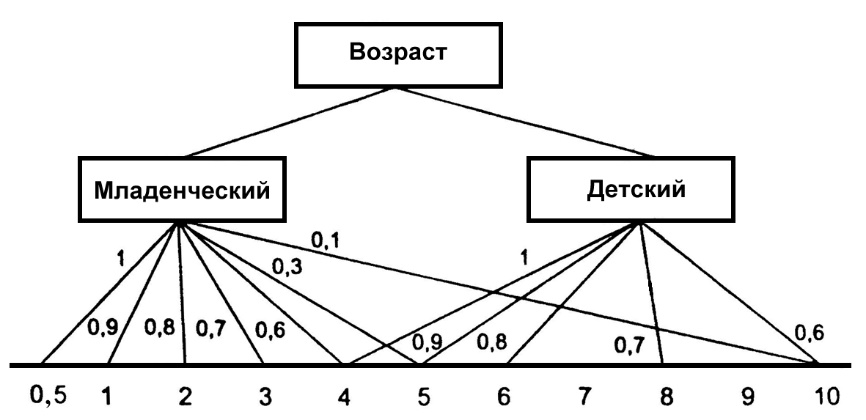
Рис. 6.2. Формирование нечетких множеств

Рис.6.3 иллюстрирует оценку НМ неким усредненным экспертом, который ребенка до полугода с высокой степенью уверенности относит к младенцам (m=1). Дети до четырех лет причисляются к младенцам тоже, но с меньшей степенью уверенности (0.5


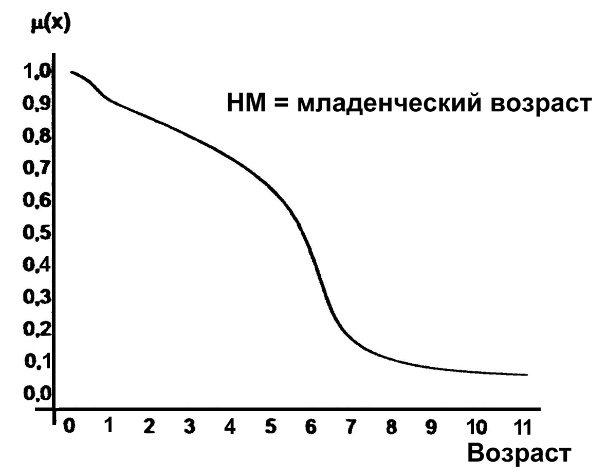
Рис. 6.3. График функции принадлежности нечеткому множеству «младенческий возраст».

Основные характеристики нечетких множеств

Пусть М = [0,1] и A – нечеткое множество с элементами из универсального множества Е и множеством принадлежностей М.

• 
  Величина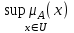 называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна 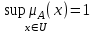. При 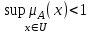нечеткое множество называется субнормальным.
  
• 
  Нечеткое множество пусто, если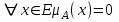 . Непустое субнормальное множество можно нормализовать по формуле:
  

.

• 
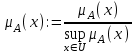  Нечеткое множество унимодально, если µ_А(х) = 1 только на одном х из Е.
  
• 
  Носителем нечеткого множества А является обычное подмножество со свойством µ_А(х)>0, т.е. носитель
  

---

.

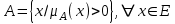Элементы х Е, для которых µ_А(х) = 0.5, называются точками перехода множества А.
Нечеткие числа – нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности 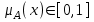, где .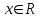

Нечеткое число А нормально, если 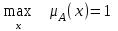, и выпуклое, если для любых 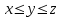выполняется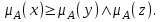




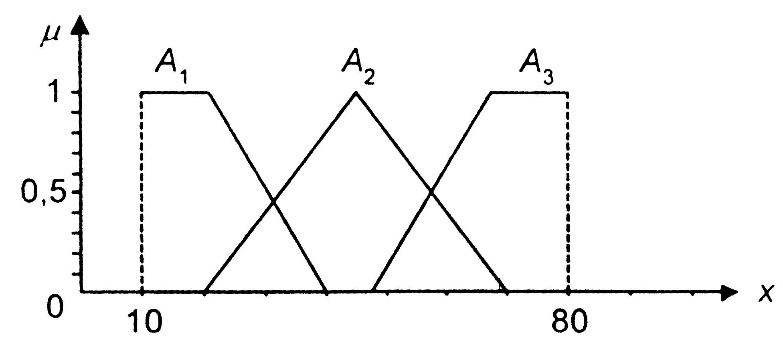
Рис. 6.4. Функции принадлежности нечетких множеств:

А₁ – «малая толщина»; А₂ – «средняя толщина»;

А₃ – «большая толщина»
Нечеткие правила вывода

Базовое правило вывода типа "если - то" (англ.: if- then rule)называется также нечеткойимпликацией, принимающей форму

если х это А, то у это В (6.1)

где А и В - это лингвистические значения, идентифицированные нечетким способом через соответствующие функции принадлежности для переменных х и у. Часть "х это А" называется условием (предпосылкой),а "у это В" - следствием (заключением). Импликацию (6.1) можно записать в сокращенном виде А → В. Нечеткое рассуждение - это процедура, которая позволяет определить заключение, вытекающее из множества правил "если - то". Такое множество при N переменных х может принять вид

если x₁это А₁ и х₂ это А₂ и ... и x_N это A_N, тo у это В (6.2)

Переменные x₁, x₂, …,x_Nобразуют N-мерный входной вектор x, составля­ющий аргумент условия, в котором А₁, А₂ , ..., A_nи В обозначают величины соответствующего коэффициента принадлежности

---

, . Необходимо обратить внимание, что здесь присутствуют индивидуальные функции принадлежности для каждой переменной х_i, и отдельно для y. Случайное значение функции принадлежности , где х - это вектор х = [ x₁, x₂, …,x_N]отно­сящееся к условию импликации (уровень активации правила), должно в последующем интерпретироваться с использованием введенных ранее нечетких операций. Возможна интерпретация (то есть определение уровня активации (нечеткого значения) переменной, указанной в следствии правила) в форме логического произве­дения множеств либо в форме алгебраического произведения:

1. 
   интерпретация в форме логического произведения (из всех нечетких значений переменных условия правила берется минимальное):
   

(6.3)

2. 
   интерпретация в форме алгебраического произведения (в качестве нечеткого значения переменной следствия правила берется значение, полученное путем перемножения нечетких значений переменных условия правила):
   

(6.4)

Приписывание единственного значения функции принадлежности, описы­вающей многомерное условие, будем называть агрегированием предпосылки. Каждой импликации А → В, определенной выражением (6.2), можно приписать также единственное значение функции принадлежности . Наиболее популярные интерпретации этой функции также имеют форму логического или алгебраического произведения:

• 
  форма логического произведения
  

(6.5)

• 
  форма алгебраического произведения
  

---

(6.6)

Приписывание единственного значения функции принадлежности всей импликации будем называть процедурой агрегирования на уровне импликации.
Нечеткий логический вывод

Системы нечеткого вывода Мамдани-Заде

Элементы теории нечетких множеств, правила импликации и нечетких рассуждений образуют систему нечеткого вывода. В ней можно выделить множество используемых в системе нечетких правил, базу данных, содер­жащую описания функций принадлежности, а также механизм вывода и агрегирования, который формируется применяемыми правилами импликации. Следует упомянуть, что в случае технической реализации в качестве вход­ных и выходных сигналов выступают измеряемые величины, однозначно сопоставляющие входным значениям соответствующие выходные зна­чения. Для обеспечения взаимодействия множеств этих двух видов вводится нечеткая система с так называемыми фазификатором (преобразо­вателем множества входных данных в нечеткое множество) на входе и дефазификатором (преобразователем нечетких множеств в конкретное значение выходной переменной) на выходе. Структура такой системы представлена на рис.6.5.



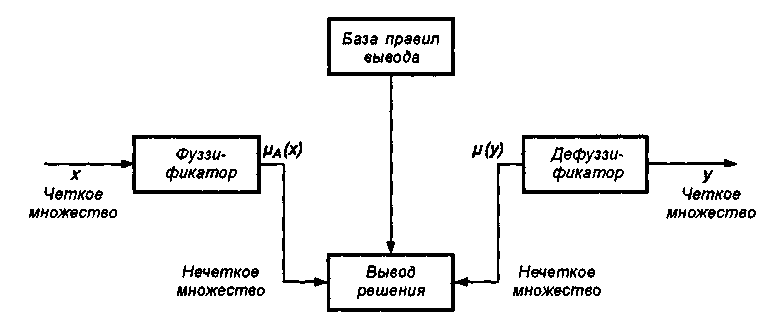
Рис. 6.5. Структура нечеткой системы с фазификатором и дефазификатором
Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида:

П₁: если х есть A₁, то у есть В₁

П₂: если х есть А₂, то у есть В<sub>2

……………………</sub>

П_n: если х есть Аn, то у есть В_n ,

где х – входная переменная (имя для известных значений данных); у – переменная вывода (имя для значения данных, которое будет вычислено); А и В – функции принадлежности, определенные соответственно на х и у.

Приведем более детальное пояснение Знание эксперта A → В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через R:

R = A → В,

где «→» называют нечеткой импликацией.

Отношение R можно рассматривать как нечеткое подмножество прямого произведения X × Y полного множества предпосылок X и заключений Y. Таким образом, процесс получения (нечеткого) результата вывода B' с использованием данного наблюдения А' и знания А→В можно представить в виде композиционного правила

---

Смотрите также файлы

• Фамилия, имя, отчество обучающегося.docx

• Программа speccy.docx

• Тема Развитие школьных команд технологии межпредметного сотрудничества и функциональная грамотность.doc

• Исследование физических характеристик, сохраняющихся при столкновениях.docx

• Методические рекомендации по выполнению и защите индивидуального проекта Для обучающихся всех специальностей.docx