ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.04.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание №5 Многофакторный регрессионный анализ
На основе заданного массива данных построить уравнение регрессии в виде линейного алгебраического полинома от двух переменных, проверить его адекватность и значимость факторов. Расчёты произвести в матричной форме.
Порядок выполнения задания.
1. Выполнить центрирование факторов
2. Составить матричное уравнение с вектором неизвестных оценок коэффициентов регрессии.
3. Найти решение матричного уравнения - оценки коэффициентов регрессии.
4. Проверить адекватность построенного уравнения регрессии экспериментальным данным по критерию Фишера при уровне значимости α = 0,05.
5. Выполнить селекцию факторов по критерию Стьюдента при таком же уровне значимости.
6. Повторно проверить адекватность уравнения регрессии после исключения незначимых факторов.
Таблица 1. Исходные данные
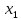 | 1 | 0,5 | 3 | 2 | 1 | -2 |
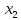 | 1 | 2 | 2 | 3 | 0,3 | 0,5 |
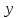 | 2 | 4,3 | 7,2 | 8 | 0 | -3 |
Решение
-
Выполнить центрирование факторов
Факторы считаются центрированными, если
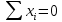. Если данное условие не выполняется, то необходимо сдвинуть центр. Для этого из каждого значения необходимо вычесть их среднее арифметическое 
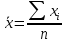.Рассчитаем среднее арифметическое для каждого фактора.
Таблица 2. Среднее арифметическое
| № | 1 | 2 | 3 | 4 | 5 | 6 | Сумма | Среднее |
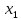| | 1 | 0,5 | 3 | 2 | 1 | -2 | 5,5 | 0,92 |
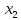| | 1 | 2 | 2 | 3 | 0,3 | 0,5 | 8,8 | 1,47 |
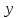| | 2 | 4,3 | 7,2 | 8 | 0 | -3 | 18,5 | 3,08 |
Таблица 3. Центрированные факторы
| № | 1 | 2 | 3 | 4 | 5 | 6 | Сумма |
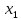| | 0,08 | -0,42 | 2,08 | 1,08 | 0,08 | -2,92 | 0 |
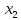| | -0,47 | 0,53 | 0,53 | 1,53 | -1,17 | -0,97 | 0 |
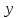| | -1,08 | 1,22 | 4,12 | 4,92 | -3,08 | -6,08 | 0 |
2. Составить матричное уравнение с вектором неизвестных оценок коэффициентов регрессии.
Уравнение множественной регрессии представляет собой зависимость объясняемой переменной Y от нескольких объясняющих переменных X:
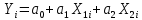
Систему можно записать в матричном виде:
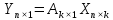
3. Найти решение матричного уравнения - оценки коэффициентов регрессии.
Согласно методу наименьших квадратов, вектор A получается из выражения:
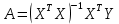
К матрице с переменными Xj добавляем единичный столбец:
| 1 | 0,08 | -0,47 |
| 1 | -0,42 | 0,53 |
| 1 | 2,08 | 0,53 |
| 1 | 1,08 | 1,53 |
| 1 | 0,08 | -1,17 |
| 1 | -2,92 | -0,97 |
Матрица Y
| -1.08 |
| 1.22 |
| 4.12 |
| 4.92 |
| -3.08 |
| -6.08 |
Находим транспонированную матрицу
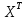
| 1,00 | 1,00 | 1,00 | 1,00 | 1 | 1 |
| 0,08 | -0,42 | 2,08 | 1,08 | 0,08 | -2,92 |
| -0,47 | 0,53 | 0,53 | 1,53 | -1,17 | -0,97 |
Умножаем матрицы
| = |
| |
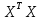
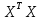Умножаем матрицы
| = |
| |
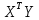
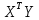Находим обратную матрицу
| = |
| |
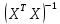
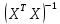Вектор оценок коэффициентов регрессии равен
| Y(X) = |
| * |
| = |
| |
Уравнение регрессии (оценка уравнения регрессии)
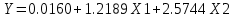
4. Проверить адекватность построенного уравнения регрессии экспериментальным данным по критерию Фишера при уровне значимости α = 0,05.
Матрица A, составленная из Y и X:
| 1 | -1.08 | 0.08 | -0.47 |
| 1 | 1.22 | -0.42 | 0.53 |
| 1 | 4.12 | 2.08 | 0.53 |
| 1 | 4.92 | 1.08 | 1.53 |
| 1 | -3.08 | 0.08 | -1.17 |
| 1 | -6.08 | -2.92 | -0.97 |
Транспонированная матрица.
| 1 | 1 | 1 | 1 | 1 | 1 |
| -1.08 | 1.22 | 4.12 | 4.92 | -3.08 | -6.08 |
| 0.08 | -0.42 | 2.08 | 1.08 | 0.08 | -2.92 |
| -0.47 | 0.53 | 0.53 | 1.53 | -1.17 | -0.97 |
Матрица
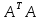.| 6 | 0.02 | -0.02 | -0.02 |
| 0.02 | 90.288 | 30.792 | 20.367 |
| -0.02 | 30.792 | 14.208 | 5.233 |
| -0.02 | 20.367 | 5.233 | 5.433 |
Полученная матрица имеет следующее соответствие:
| ∑n | ∑y | ∑x1 | ∑x2 |
| ∑y | ∑y2 | ∑x1 y | ∑x2 y |
| ∑x1 | ∑yx1 | ∑x12 | ∑x2 x1 |
| ∑x2 | ∑yx2 | ∑x1 x2 | ∑x22 |
| |  |  |  |  |  |  |
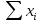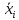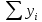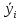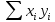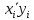| Для y и x1 | -0,02 | -0,0033 | 0,02 | 0,0033 | 30,7916 | 5,1319 |
| Для y и x2 | -0,02 | -0,0033 | 0,02 | 0,0033 | 20,3666 | 3,3944 |
| Для x1 и x2 | -0,02 | -0,0033 | -0,02 | -0,0033 | 5,2334 | 0,8722 |
