СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ «Арифметическая прогрессия»

Тема	Числовая последовательность, способы её задания и свойства. Арифметическая прогрессия. Характеристическое свойство арифметической прогрессии. Формула n-ого члена арифметической прогрессии. Формула суммы n первых членов арифметической прогрессии.
Цели обучения	9.2.3.2 Находить n-й член последовательности, например: ; ; ;.. 9.2.3.5 Знать и применять формулы n-го члена, суммы n- первых членов и характеристическое свойство арифметической прогрессии
Критерии оценивания	Обучающийся Находит значение номера члена числовой последовательности. Применяет характеристическое свойство арифметической прогрессии, находит n-й член Применяет формулу n-ого члена арифметической прогрессии. Применяет формулу суммы n первых членов арифметической прогрессии.
Уровень мыслительных навыков	Применение Навыки высокого порядка
Время выполнения	25 минут

ЗАДАНИЯ
1 ВАРИАНТ

1. 
   Числовая последовательность задана формулой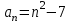 . Найдите ее шестой член.
   
2. 
   Пусть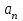 есть арифметическая прогрессия. Если а₂ =6 и а₄ =12, с помощью характеристического свойства найдите а₃.
   
3. 
   Известны два члена арифметической прогрессии (а_n), а₆ =-3 и а₁₂=9. Найдите для этой прогрессии:
   

1) первый член и разность;

2) число отрицательных членов;

---

3) первый положительный член прогрессии.

4. 
   Найдите сумму 30-и первых членов арифметической прогрессии 1,2; 1,8; 2,4; …
   

2 ВАРИАНТ

1. 
   Числовая последовательность задана формулой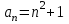 . Найдите ее шестой член.
   
2. 
   Пусть есть арифметическая прогрессия. Если а₃ =5 и а₅ =11, с помощью характеристического свойства найдите а₄.
   
3. 
   Известны два члена арифметической прогрессии (а_n), а₆ =12 и а₁₀=4. Найдите для этой прогрессии:
   

1) первый член и разность;

2) число положительных членов;

3) первый отрицательный член прогрессии.

4. 
   Найдите сумму 24-х первых членов арифметической прогрессии 1,6; 2,1; 2,6; …
   

Критерий оценивания	№ задания	Дескриптор	Балл
		Обучающийся
Находит значение номера члена последовательности.	1	Применяет формулу общего члена числовой последовательности	1
		Находит значение n-члена последовательности	1
Применяет характеристическое свойство арифметической прогрессии, находит n-й член	2	Применяет характеристическое свойство арифметической прогрессии	1
		вычисляет значение n-члена	1
Применяет формулу n-ого члена арифметической прогрессии.	3.1	находит разность прогрессии	1
	3.1	находит первый член прогрессии	1
	3.2	определяет число отрицательных членов прогрессии	1
	3.3	указывает номер первого положительного члена прогрессии и находит его значение	1
Применяет формулу суммы n первых членов арифметической прогрессии	4	записывает формулу суммы n первых членов арифметической прогрессии	1
		находит а1и аn/ а1 и d	1
		вычисляет значение суммы	1
Общий балл			11

---

---

Смотрите также файлы

• Литература к 1му разделу Философия хозяйства информационного общества Литература к 2му разделу Заключение Введение.doc

• Контрольная работа по дисциплине Транспортное право.docx

• Электроснабжение эксплуатационного депо ЮжноУральской дирекции тяги филиала оао ржд в г. Карталы Челябинской области с разработкой мероприятий по защите персонала от поражения электрическим током.docx

• Технические причины производственного травматизма. Общие понятия и определения здорового образа жизни. Связь образа жизни с профилактикой заболеваний. Значение соблюдения правил личной и общественной гигиены.docx

• Чем можно помочь Первое условие школьного успеха пятиклассника безусловное принятие ребенка.doc