Добавлен: 26.04.2024
Просмотров: 5
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 14.69.1
Насос подает жидкость из подземной ёмкости с избыточным давлением газа на поверхности жидкости. На всасывающей линии (длина l, диаметр d, трубы сварные, бывшие в эксплуатации) имеются местные сопротивления: приёмная коробка с клапаном и сеткой, колено и кран с коэффициентом сопротивления ξкр. Показание вакуумметра на входе в насос равно рv, расход жидкости Q, температура t°C.
Определить рабочую высоту всасывания насоса hвс и предельную высоту из условия отсутствия кавитации на входе в насос. Объяснить также, почему при кавитации насос не всасывает жидкость и рабочее колесо насоса выходит из строя.
Рисунок к задачам 1, 2, 3, 4, 5
Таблица исходных данных
| Вариант | l, м | d, м | рv, кПа | ξкр | ри, кПа | Q, л/c | t, ºС | Жидкость |
| 1 | 9 | 0,05 | 20 | 8 | -20 | 5 | 30 | бензин |
Решение
Составляем уравнение Бернулли для сечений 1-1, проходящему по свободной поверхности жидкости в подземной емкости и сечению 2-2, проходящему в месте установки вакуумметра. Плоскость сравнения проводим по сечению 0-0 (рисунок 1):
(1)где
, 
- высоты центров тяжести сечений относительно плоскости отсчета 0-0, м; 
, 
- абсолютные давления в сечениях 1-1 и 2-2, Па; 
- плотность бензина при температуре 
,
; g – ускорение свободного падения, 
; 
, 
- средние скорости в сечениях, 
; 
- коэффициенты Кориолиса для турбулентного режима движения (в процессе решения задачи режим будет проверен); 
- суммарные потери напора между сечениями 1-1 и 2-2, м.
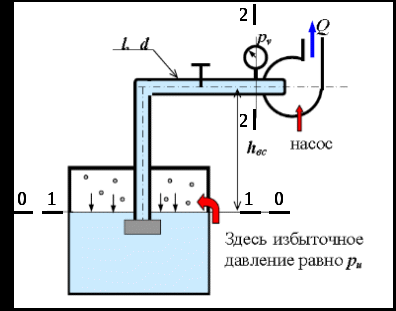
Рисунок 1
Скорость изменения уровня жидкости в подземной емкости пренебрежимо мала по сравнению со скоростью в трубопроводе, поэтому принимаем
и 
, тогда уравнение Бернулли принимает вид:
(2)откуда находим рабочую высоту всасывания насоса
(3)Число Рейнольдса:
(4)где
- коэффициент кинематической вязкости бензина при 
(справочная величина), 
;
Так как полученное значение больше критического числа Рейнольдса 2300. то режим течения турбулентный и значение
в уравнении Бернулли принято верно.Суммарные потери напора между сечениями 1-1 и 2-2:
(5)где
- коэффициент местного сопротивления приёмной коробки с клапаном и сеткой при 
(справочная величина);
- коэффициент местного сопротивления колена (справочная величина);Заменяя в выражении (3) величину
правой частью выражения (5), получаем:
(6)Вынесем
за скобки:
(7)Средняя скорость движения жидкости в трубопроводе:
(8)Заменяя в выражении (7) величину
правой частью выражения (8), получаем:
(9)Коэффициент гидравлического трения для турбулентного режима движения определяем по формуле Альтшуля:
(10)где
- эквивалентная шероховатость труб сварных, бывших в эксплуатации (справочная величина), мм;
Плотность бензина при
:
(11)где
- плотность бензина при 
(справочные данные),
;
- коэффициент температурного расширения, 
;
- разность температур, 
;
По формуле (9) находим:
Знак «минус» указывает на то, что насос должен быть установлен на 8,72 м ниже уровня жидкости в подземной емкости, то есть работать под заливом.
Для определения предельной высоты всасывания насоса из условия отсутствия кавитации на входе в насос принимаем в уравнении Бернулли абсолютное давление в сечении 2-2 равное давлению насыщения бензина при
: 
.Тогда уравнение Бернулли запишется в виде
(12)откуда
(13)С учетом преобразований полученных выше выражение (13) можно привести к виду:
(14)Принимая величину атмосферного давления равной
, находим:
Явление кипения жидкости при давлениях меньших атмосферного и равных давлению насыщенного пара, при нормальных температурах (10°, 20°,30°,.....), сопровождающееся схлопыванием пузырьков пара в областях повышенного давления, называется кавитацией.
Кавитация - вредное явление. Рассмотрим следствия кавитации на примере работы сифона. Пузырьки пара, выделяющиеся при кавитации, разрывают межмолекулярные связи, поток жидкости при этом теряет сплошность, столб жидкости на восходящей линии сифона и процесс всасывания прекращается. Кроме того, пузырьки пара, продвигаясь вместе с жидкостью дальше на нисходящую линию сифона, где давление больше давления насыщенного пара, лопаются. Аналогичные явления наблюдаются во всасывающем трубопроводе насоса.
При схлопывании пузырька на твердой поверхности трубы жидкость, устремившаяся в освободившееся пространство, останавливается. При этом ее кинетическая энергия превращается в потенциальную и происходят местные гидравлические удары. Это явление сопровождается существенным ростом давления и температуры и приводит к разрушению материала трубопровода и насоса.
Ответ: hвс 8,72 м, hвс.пр 5,47 м.