Ламинарлы қозғалыста ұзына бойындағы арын шығыны қандай формуламен анықталады, қорытып шығарыңыз

Ламинарлы қозғалыс деп отырғанымыздың өзі егер сұйық қозғалысы белгілі бір реттілікті сақтап отырып бір бірімен әрекеттессе, ламинарлы (латын тілінде lamina - қабат) тәртіпке сәйкес келеді.Яғни,ламинарлы тәртіп сұйық бөліктерінің параллель ағысты тәртіпті қозғалысын сипаттайды, ағынның жай қабатты қозғалысы болып келеді.

Кез келген сұйықтың қозғалысы гидравликалық кедергіге және арын шығынына тығыз байланысты болып келеді, сол себепті де сұйықтың қозғалысына бағытталған есептерді шешу кезінде сұйық ағынның қозғалыс барысын жалпы бір бірімен әрекеттесу реттілігін біліп алуымыз қажет.

Арын шығынын Q қорытып шығару үшін ағын арнасының көлденең қимасынан сақиналы пішінді радиусы у және ені dy элементарлы кішкентай қимыл қиманы бөліп аламыз .Осы қимадағы сұйықтың элементарлы шығыны

dQ  Ud

бұл жердегі: U - сақиналы қимадағы сұйық жылдамдығы; d - элементарлы қимыл қима болып келеді

d  2ydy

Айнымалыларға қатысты теңдеу келесі түрде болады:



мұндағы P1 және P2 сәйкесінше 1 және 2 бөлімдердегі қысымдар.

Құбыр қабырғаларында r = R, , мәні жылдамдық υ = 0, ал r = 0 кезінде (ағын осінде) жылдамдық максималды болады.



Енді дөңгелек құбырдағы ламинарлы ағындағы сұйықтың шығынын анықтайық. Дөңгелек құбырдағы жылдамдықтардың таралу диаграммасы құбырдың центрінде максималды жылдамдығы бар айналу параболоиды түріне ие болғандықтан, сұйықтықтың ағу жылдамдығы осы параболоидтың көлеміне сандық түрде тең. Осы көлемді анықтайық.

Максималды жылдамдық параболоидтың биіктігін береді





Біздің формула бойынша ламинарлы қозғалыстағы арын шығыны теңдеуін келесі түрде жазамыз:



Егер біз R орнына құбыр диаметрін d қойып жазатын болсақ, онда:

---

Ламинарлы қозғалыс кезіндегі арын шығыны келесі түрде жазылады:



Бұл жердегі орташа жылдамдық негізгі түрде:



Қорыта келгенде ламинарлы қозғалыс кезіндегі арын шығынын көрсету үшін,қимыл қимадағы жылдамдықтың таралу заңын сонымен бірге теңдеудегі аргументтің өзгеру шегін 0  y  r қарастыруымыз қажет ,осы функцияларды білусұйық шығыны бойынша формуланы жаза аламыз:



Алынған теңдеу ламинарлы қозғалыс тәртібі кезіндегі гидравликалық

кедергілер заңының математикалық теңдеуі болып табылады.

Жалпы бұл формула бойынша , орташа жылдамдықтың максимальды жылдамдыққа қатынасы бұл бізде жылдамдықтар жолағының коэффициенті деп аталады , Бұл коэффицент ламинарлы тәртіп кезінде теңдеулерге сәйкес   0,5 болып келеді

Гидравликалық тегіс және кедір–бұдырлы құбырларды қалай ажыратуға болады?

Ламинарлық ағын үшін гидравликалық кедергіден қысымның жоғалуы тек бірінші дәрежеге дейінгі ағын жылдамдығының шамасына тәуелді деген тұжырымның дұрыстығын көптеген эксперименттік зерттеулер растады. Сәйкесінше гидравликалық үйкеліс коэффициенті:



Бізде құбырларды қарастыру кезінде оның ламинарлы қабат қалыңдығына және де абсолютті кедір-бұдырлық қатынасына байланысты оларды гидравликалық тегіс және гидрафликалық кедір- бұдырлы деп бөліп қарастыра аламыз.

Егер ламинарлы қабаттың жолдары толықтай құбыр қабырғасын жауып тұрған болса, яғни δ >  , онда біз қарастырған құбырлар гидравликалық тегіс болып табылады. Гидравликалық тегіс құбыр кезінде Re < 10⁵ болып келеді, жасалынған тәжірибе бойынша λ шамасын анықтауда келетін қолданылатын формулалардың бірі Блазиус формуласы болып табылады.Оны келесі түрде жаза аламыз:



Ал қарастырып отырған жағдай керісінше болса ,яғни егер δ<Δ , болса онда құбыр гидравликалық кедір – бұдырлы деп есептелінеді. Гидравликалық кедір бұдырлы құбыр кезінде λ мәні негізінен қабырғаның салыстырмалы кедір – бұдырлығына байланысты болып келеді. Мұнда көбінесе жиі қолданылатын формулалардың бірі Б.Л.Шинфринсон формуласы:

---

Бұл жердегі Δ кедір – бұдырлықтың кертеші биіктігі , оны  - абсолютті кедір бұдырлық деп атайды

Турбулентті қозғалыс кезінде барлық жағдайды жан жағынан қарастыра алатын қамти алатын әмбебап формуланың бірі А.Д.Альтшуль формуласы болып келеді.Ол бізде келесі түрде жазылатын болады:



Турбулентті қозғалыс кезіндегі берілген А.Д.Альшуль формуласы бойынша келесі теңдіктерді көрсетіп кете аламын.Бұлар құбырлардығ гидрафликалық тегіс немесе кедер бұдырлы сипатта болуын айқындайды.

Егер бізде Re˂ 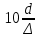болса, онда құбырлар гидравликалық тегіс болып табылады,себебі

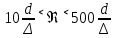осы теңдік бойынша, λ шамасы Рейнольдс саны сияқты құбырдың салыстырмалы кедір – бұдырлығына өз әсерін тигізеді; Ал егер 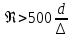болса, онда құбырлар гидравликалық кедір – бұдырлы болып табылады

Қорыта айтқанда λ шамасы  мен Re сандарына тығыз байланысты сондықтан да құбырдың гидрвликалық тегіс және кедір бұдыр болуы осы шамаларға байланысты болып келеді Яғни (  - тің бір мәнімен) гидравликалық тегіс ( Re кіші кезде), кедірбұдырлы ( Re үлкен болғанда) болып келеді.

Турбулентті режим құрылымы қандай? Бұл режимдегі ламинарлы қабат қалыңдығы қалай анықталады?

Турбуленттік - сұйық бөлшектерінің өте күрделі траекториялар бойынша қозғалысының ретсіз сипаты байқалатын қозғалыс латынның turbulentus – құйынды, хаотикалық сөзінен шыққан.

Турбулентті - сұйықтың қозғалысы, оның бөлшектері біршама күрделі траекториялар бойынша тұрақсыз және ретсіз қозғалыстар жасайды, нәтижесінде сұйықтықтың әртүрлі қабаттары қарқынды араласады.Яғни ,турбулентті қозғалыс – тұрақсыз қозғалыс болып келеді.

Сұйықтықтың турбулентті қозғалысының айрықша белгісі ағындағы бөлшектердің ретсіз қозғалысы болып табылады. Дегенмен, мұндай қозғалыста кейбір заңдылықты жиі байқауға болады. Өлшеу нүктесіндегі жылдамдықтың өзгеруін жазуға мүмкіндік беретін термогидрометрді пайдаланып, жылдамдық қисығын алуға болады. Егер біз жеткілікті ұзақтықтағы уақыт аралығын таңдасақ, онда жылдамдықтың ауытқуы белгілі бір деңгейдің айналасында байқалатыны және әртүрлі уақыт интервалдарын таңдау кезінде бұл деңгей тұрақты болып қалатыны белгілі болады. Берілген уақытта берілген нүктедегі жылдамдық шамасы лездік жылдамдық деп аталады.

---

Егер жылдамдық қисығында белгілі бір уақыт аралығын таңдап, жылдамдық қисығын біріктіріп, содан кейін орташа мәнді тапсақ, онда бұл шама орташа жылдамдық деп аталады

Лездік және орташа жылдамдық арасындағы айырмашылық пульсация жылдамдығы u' деп аталады.



Егер әр түрлі уақыт аралықтарындағы орташа жылдамдықтар тұрақты болып қалса, онда сұйықтықтың мұндай турбулентті қозғалысы тұрақты болады.

Сұйықтықтың пульсациясы сұйықтықтың ағынға араласуының себебі болып табылады. Араластыру қарқындылығы, өзіңіз білетіндей, Рейнольдс санына байланысты, яғни.басқа жағдайларды сақтау кезінде сұйықтықтың жылдамдығына байланысты. Осылайша, нақты ағымда сұйықтық (сұйықтықтың тұтқырлығы және қиманың өлшемдері бастапқы шарттармен анықталады) оның қозғалыс сипаты жылдамдыққа байланысты. Турбулентті ағын үшін бұл өте маңызды. Сонымен, сұйықтықтың перифериялық қабаттарында жылдамдық әрдайым минималды болады, және бұл қабаттардағы қозғалыс режимі табиғи түрде ламинарлы болады. Жылдамдықты критикалық мәнге дейін арттыру сұйықтықтың қозғалыс режимін ламинарлық режимнен турбулентті режимге ауыстыруға әкеледі. Яғни, нақты ағымда ламинарлық және турбулентті режимдер де бар.

Сұйықтың турбулентті қозғалыс тәртібі табиғатта және техникада көбірек таралған, соған қарамастан, бұл бірден – бір гидравликалық күрделі құбылыс болып саналады. Бұлсалада жүргізілген көптеген зерттеулерге қарамастан, осы уақытқа дейін турбулентті қозғалыс тәртібіне түпкілікті теория жасалынбаған. Сондықтан турбулентті ағындағы гидравликалық есептерді шығарғанда кейбірі жеке жартылай эмпирикалық формулалар мен тәжірибелік мәліметтер де кеңінен қолданылады.

Турбулентті ағындағы ламинарлы қабат өзінің аз шамасына қарамай үлкен роль атқарады. Оның қалыңдығы  келесі теңдеумен анықталады:



Бұл формула бойынша Re өскен сайын  азаяды, ал Re кеміген сайын  ұлғая түседі

Сұйық бөліктерінің көлденең орын ауыстыруларында турбулентті ағын ядросының болуы қосымша жанама кернеуінің пайда болуына әкеп соғады.

Гидравликалық кедергілер туралы жазыңыз және мысал келтіріңіз

---

Гидравликалық кедергі – бұл тұтқыр үйкелістің болуына байланысты гидравликалық жүйелердің учаскелерінде (гидравликалық жетек жүйелері, құбырлар, басқа да гидравликалық жабдықтар) меншікті энергияның (оны жылуға айналдыру) қайтарылмайтын жоғалтулары болып келеді.

Гидравликалық кедергілер (оларға сәйкес арын шығындары) екі түрге бөлінеді: ағынның барлық ұзындығындағы сұйық қозғалысынан пайда болатын және оның ұзындығына тікелей байланысты болатын ұзындық кедергілері; ағынның жеке бөліктерінде- әртүрлі құбыржолдық немесе арнаның (буындарда, үштіктерде, ысырмаларда, ағынның кенеттен тарылған немесе кеңейген жерлерінде және т.б.), фасондарында сұйықтың қалыпсыз қозғалысынан пайда болатын (ұзындыққа қытыссыз) жергілікті кедергілер. Дөңгелек цилиндрлік құбырдағы ағын бойындағы арын шығынын анықтау үшін Дарси- Вейсбах формуласы қолданылады:



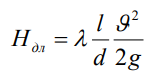
мұндағы λ – құбыр жол бойындағы кедергілерді сипаттайтын ДАРСИ коэффициенті (сұйықтың үйкеліс коэффициенті), өлшемсіз шама; l – құбыр ұзындығы; d – құбырдың сыртқы диаметрі;  - ағынның орташа жылдамдығы.



Дарси – Вейсбах формуласынан басқа гидравликада Шези формуласы да кеңінен қолданылады.



Мұндағы С- Шези коэффиценті ,оның өлшем бірлігі

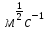
ал i-гидравликалық еңіс ,ол бізде өлшемсіз шама болып келеді

Гидравликалық кедергіні орташа жылдамдық векторының бағыты бойынша бөлуге болады.

1.Сұйықтық ағынының қозғалыс бағыты өзгермеген кезде жылдамдық өзгереді.

Мысалға қарастырсақ, құбырдың (арнаның) кеңеюін жатқыща аламыз.

2.Ағынның қозғалыс бағыты өзгерген кезде жылдамдық тұрақты болады.

Қандай теңдеуді негізге ала отырып, жазық тоспадағы ағыстың қысым күшін анықтайтын формуланы алуға болады? Қорытып шығарыңыз:
Жазық тоспа бойымен қозғалып жатырған ағыстың қысым күшін келесі көрсетілген теңдік бойынша анықтай аламыз:

---

Смотрите также файлы

• Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Иностранный язык Практическое занятие 12.rtf

• Решение Площадь смоченной поверхности треугольной крышки (1).doc

• Разъяснение субъекту персональных данных последствий отказа в предоставлении своих персональных данных для оформления трудовых отношений с Федеральной службой судебных приставов.doc

• Учетная форма 001гсу.doc

• Урок Преобразования графиков функции.docx