Файл: 1. Предмет инженерная графика. Требования, предъявляемые к чертежу. Метода построения изображений на чертеже.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 11
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Предмет инженерная графика. Требования, предъявляемые к чертежу. Метода построения изображений на чертеже.
Инженерная графика - прикладная область знаний о разработке конструкторской документации.
Объектом изучения инженерной графики является изучение геометрических свойств объектов.
 Требования к чертежу:
Требования к чертежу:-
Наглядность -
Удобоизмеряемость
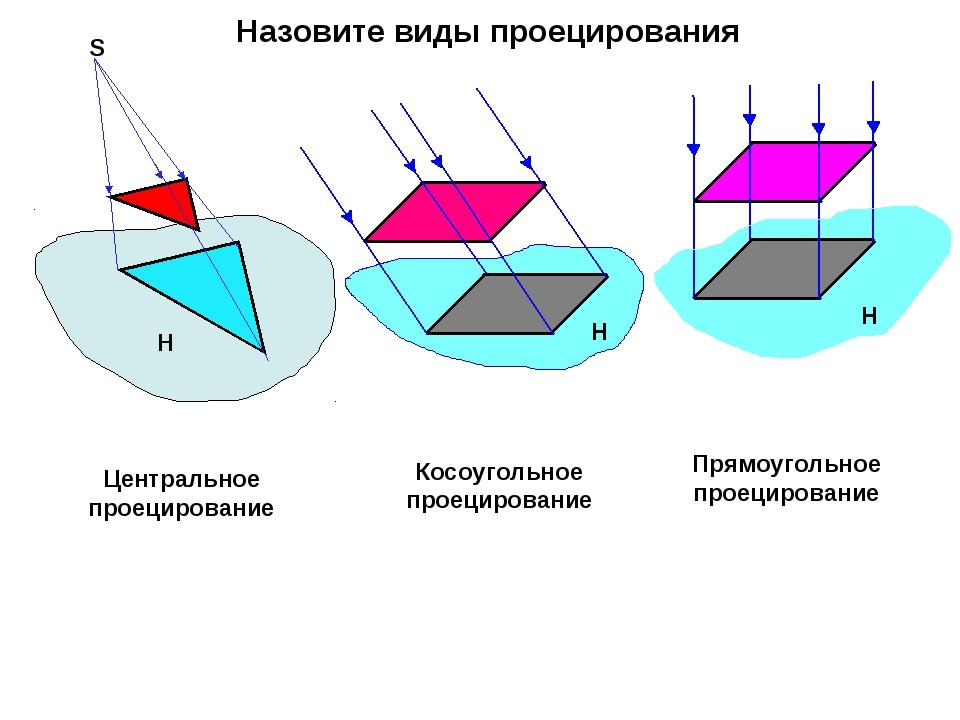
Методы проекций:
-
Параллельные:
-
Косоугольные -
Ортогональные ( прямоугольные)
-
Центральные
2. Параллельное проецирование. Инвариантные свойства параллельного проецирования.
Если проецирующие лучи параллельны друг другу, а центр проецирования удален в бесконечность, то такое проецирование называется параллельным.
Свойства параллельного проецирования:
1. Изображения точки есть единственная точка.
2. Непрерывность линии между двумя точками сокращается на изображение линии между теми же точками.
Следствие: если точка принадлежит линии, то проекция этой точки принадлежит проекции этой линии.
3. Изображение прямой есть прямая.
4. Отношение, в котором точка отрезка делит отрезок одинаково в изображении и в оригинале.
Следствие: середина отрезка изображается серединой его проекции.
5. Проекции параллельных прямых параллельны.
6
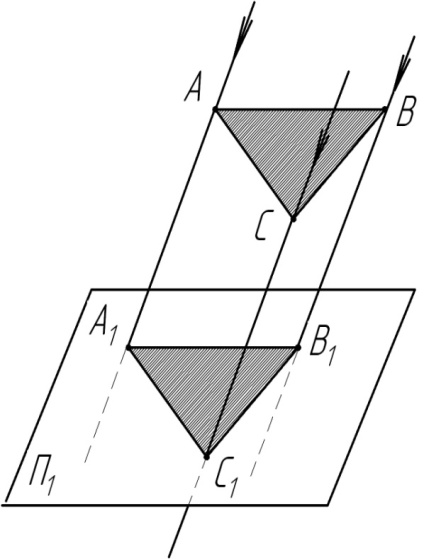 . Элементы объекта, лежащие в плоскости, параллельно плоскости проекции, изображается на ней без искажений.
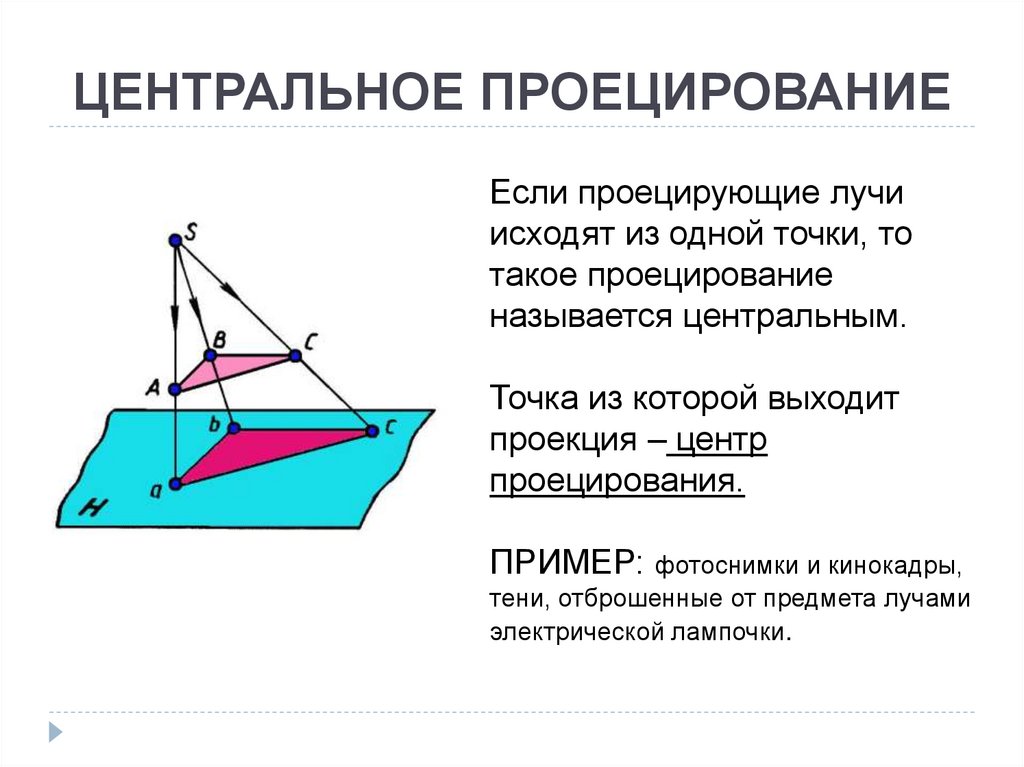
. Элементы объекта, лежащие в плоскости, параллельно плоскости проекции, изображается на ней без искажений.3. Центральное проецирование
Методом проецирования называется способ получения изображений с помощью определенной, присущей только ему совокупности средств проецирования (центра проецирования, направления проецирования, проецирующих лучей, плоскостей (поверхностей) проекций), которые определяют результат — соответствующие проекционные изображения и их свойства.
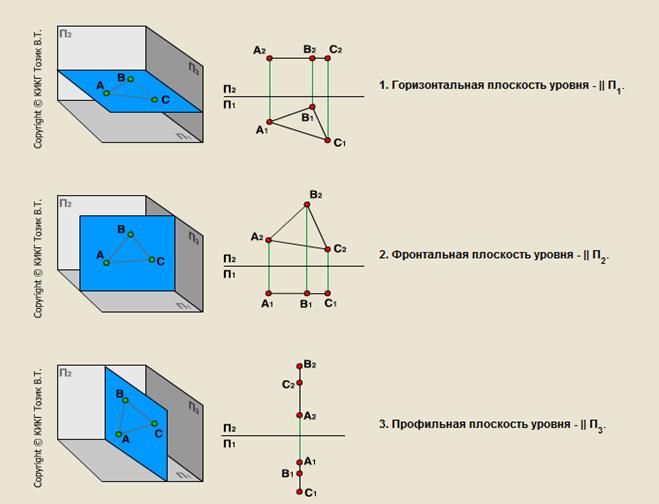
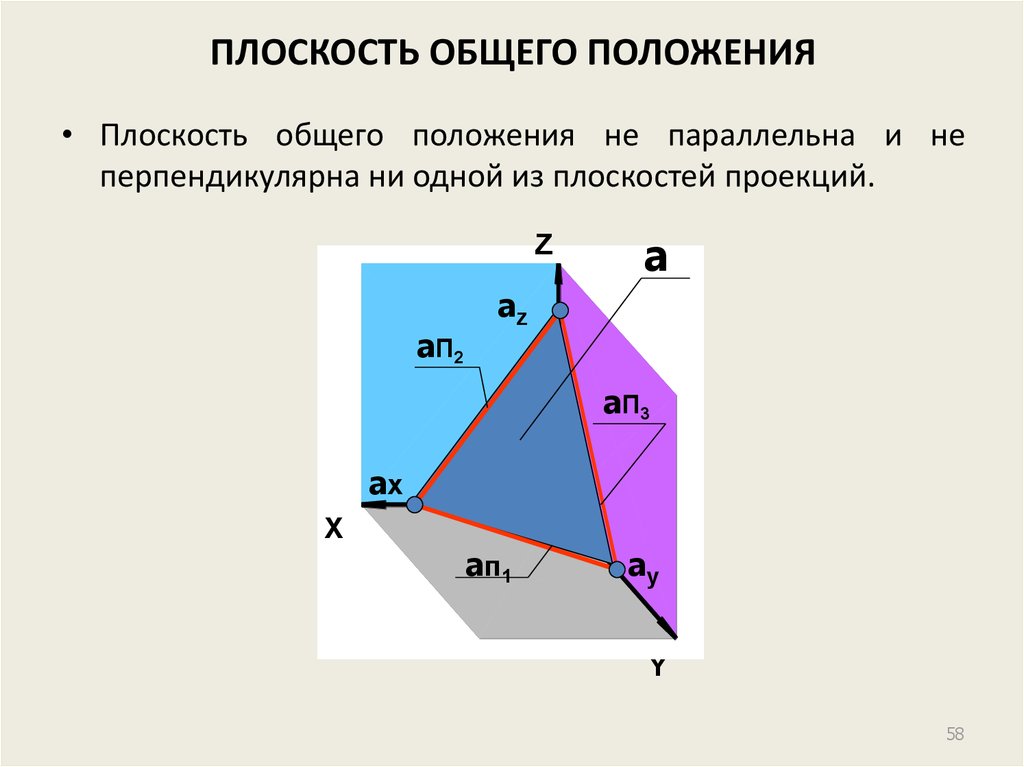
4. Плоскости уровня. Плоскости общего положения.
Плоскости уровня - плоскости параллельные плоскости проекции.
Свойство: одна проекция - истинная величина, две других отрезки прямых.
Плоскость параллельная горизонтальной плоскости проекции называется горизонтальной плоскостью уровня.
Плоскость параллельная фронтальной плоскости проекции называется фронтальной плоскостью уровня.
Плоскость параллельная профильной плоскости проекции называется профильной плоскостью уровня.
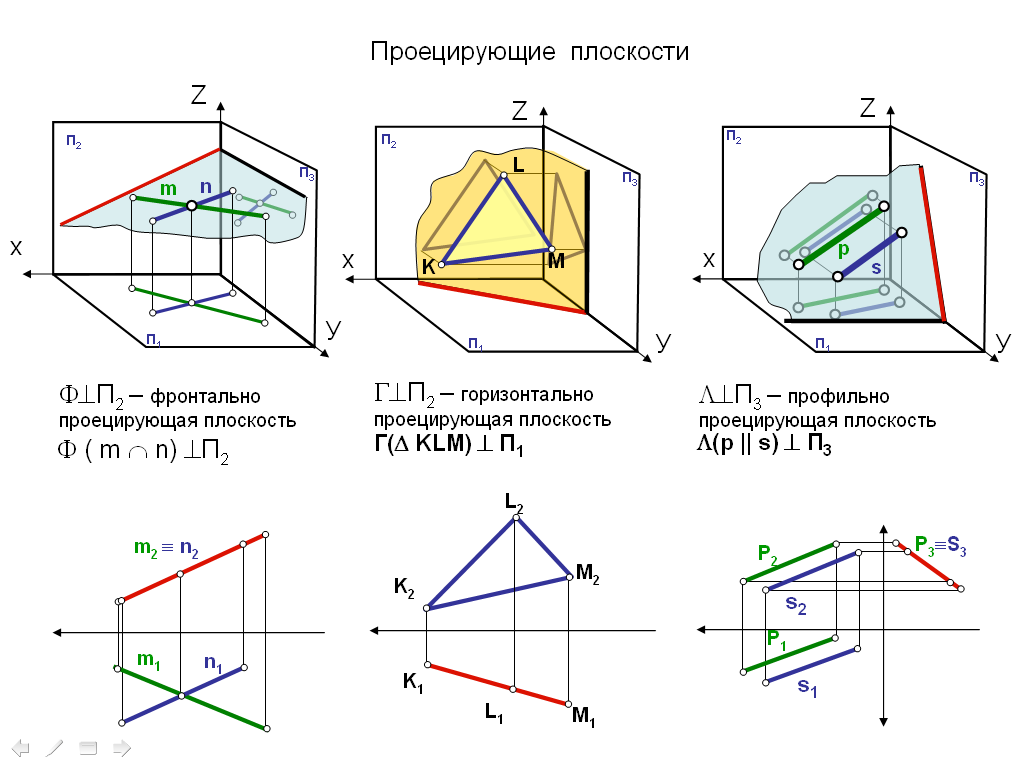
5. Проецирующие плоскости. Плоскости общего положения.
Проецирующие плоскости - плоскости перпендикулярные одной плоскости проекции.
Свойство: отображается отрезком прямой на той плоскости, которой перпендикулярна. На двух других изображается в искаженном виде, но сохраняет геометрическую форму.
Плоскость перпендикулярная горизонтальной плоскости проекции называется горизонтально-проецирующей плоскостью.
Плоскость перпендикулярная фронтальной плоскости проекции называется фронтально-проецирующей плоскостью.
Плоскость перпендикулярная профильной плоскости проекции называется профильно-проецирующей плоскостью.

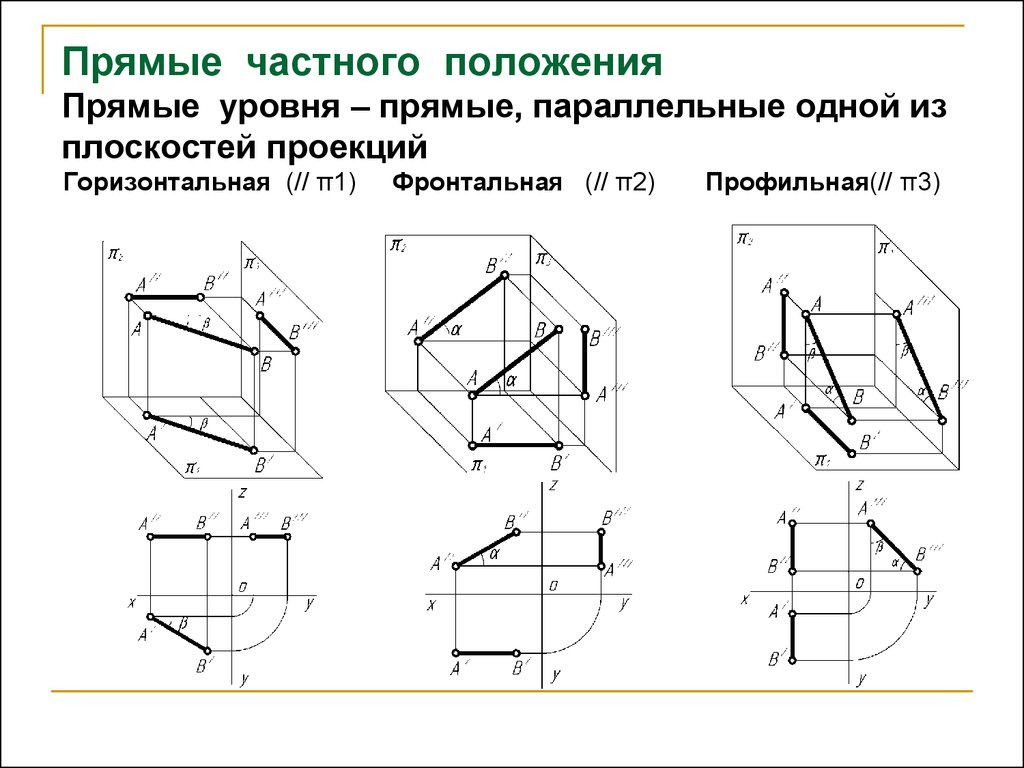
6. Прямые уровня
Прямые уровня – прямые, параллельные одной из плоскостей проекции и наклонные к двум другим.
Свойства:
-
Одна проекция – истинная величина, две другие – отрезки прямых, параллельные осям. -
Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции параллельны осям проекций. -
Если прямая перпендикулярна плоскости проекции, то ее проекцией на эту плоскость является точка, а вторая проекция, перпендикулярная осям проекций.
Прямые уровня:
-
Горизонтальная прямая – прямая параллельная горизонтальной плоскости проекций. -
Фронтальная прямая- прямая параллельная фронтальной плоскости проекций. -
Профильная прямая –прямая параллельная профильной плоскости проекций.
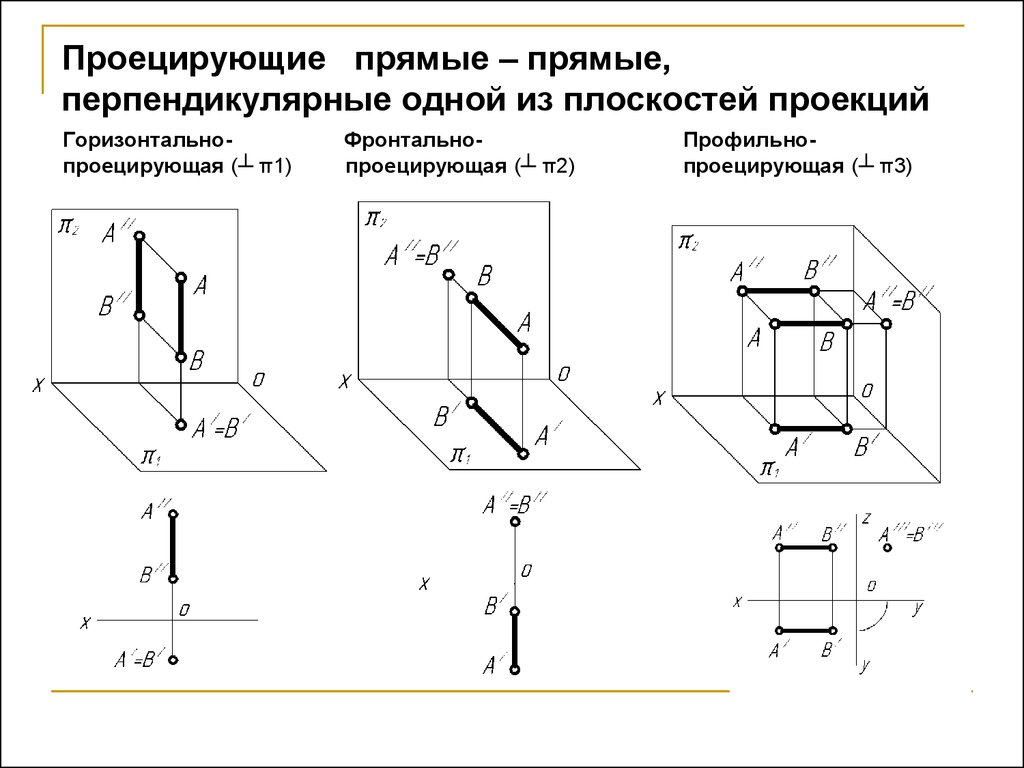
7. Проецирующие прямые
Проецирующие прямые – прямые перпендикулярные какой-либо плоскости проекции.
Свойства:
1)Две проекции – истинная величина, на третьей плоскости проекции прямая проецируется в точку, так как она перпендикулярна плоскости проекции.
Проецирующие прямые:
-
Горизонтально проецирующая прямая – прямая перпендикулярная горизонтальной плоскости проекции. -
Фронтально проецирующая прямая – прямая перпендикулярная фронтальной плоскости проекции. -
Профильно - проецирующая прямая – прямая перпендикулярная профильной плоскости проекции.
8. Виды. Основные и дополнительные виды. Понятие главного вида и схема расположения видов.
Вид - ортогональная проекция, обращенная к наблюдателю в видимой части поверхности предмета, расположенная между ним и плоскостью проецирования. (ГОСТ 2.305 - 2008)
Дополнительный вид получается проецированием предмета на плоскость не параллельную ни одной из плоскостей проекции.
Применяется в случаях, когда отдельные плоскости проецируются с искажением. Обозначается буквами русского алфавита, а у связанного с ним основного вида ставится стрелка, указывающая направление проецирования.
Виды:
1. Вид спереди
2. Вид сверху
3. Вид слева
4. Вид справа
5. Вид снизу
6. Вид сзади
Основные виды: спереди, сверху, слева.
Главный вид - вид, который дает наибольшую информацию о форме и размерах предмета.
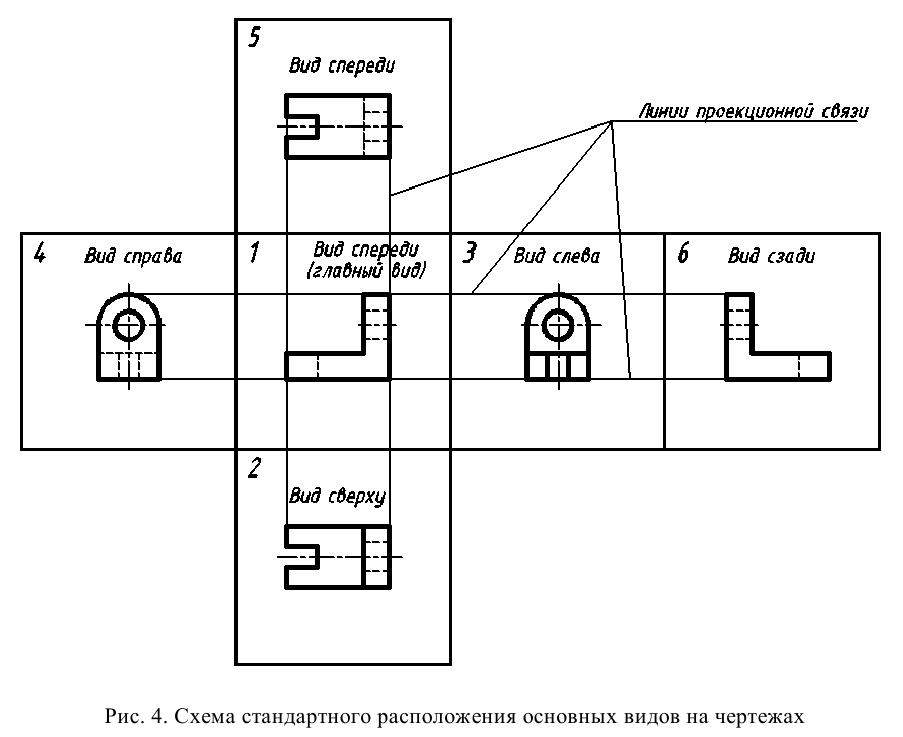
9. Виды. Требования ГОСТ 2.305-2008 к расположению видов
Виды:
1. Вид спереди
2. Вид сверху
3. Вид слева
4. Вид справа
5. Вид снизу
6. Вид сзади


10. Дополнительный вид. Порядок построения. Обозначение дополнительных видов.
Дополнительный вид получается проецированием предмета на плоскость не параллельную ни одной из плоскостей проекции.
Применяется в случаях, когда отдельные плоскости проецируются с искажением. Обозначается буквами русского алфавита, а у связанного с ним основного вида ставится стрелка, указывающая направление проецирования.
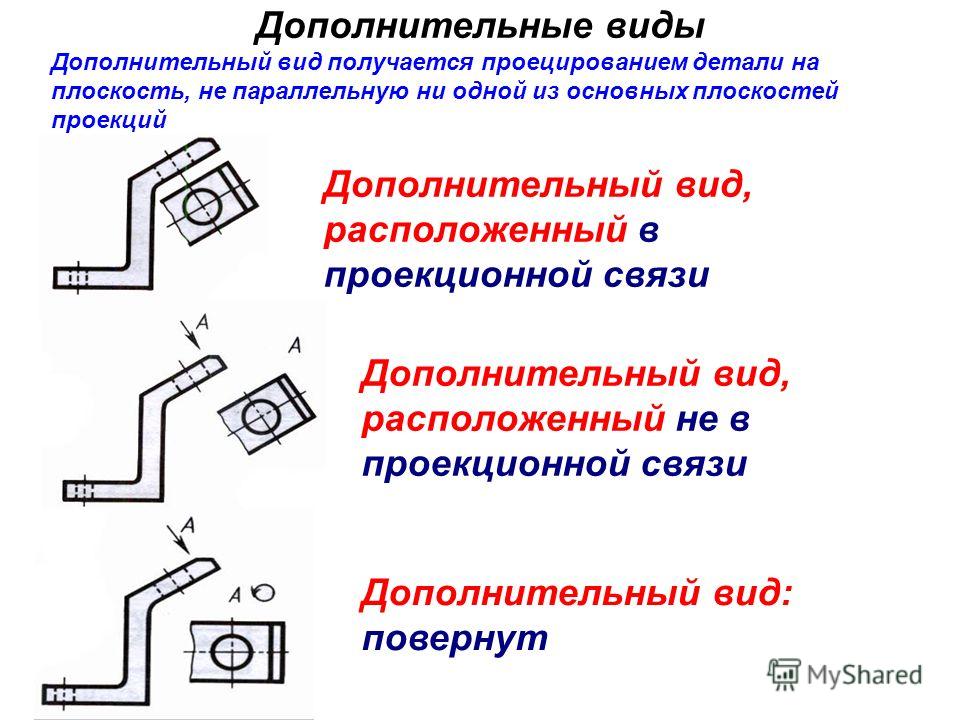
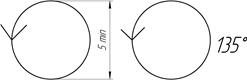
Алгоритм построения:
1) Найти вид, где плоскость будет проецироваться в отрезок прямой.
2) Отметить характерные точки; отметить проекции точек на другом изображении.
3) Провести линии проекционной связи перпендикулярно проекции плоскости на том виде, где она проецируется.
4) Обозначить проекции осей, закрепленных за плоскостью, на которых строим доп. вид.
5) Построить координаты характерных точек.
6) Соединить точки в логической последовательности.
11. Поверхности. Определитель поверхности. Каркасные линии поверхности
Поверхность - это множество положений, образующих l, перемещающихся в пространстве по определенному закону.
В качестве образующих могут использоваться прямые и кривые линии.
Закон перемещения образующих может быть задан линиями другого направления. Эти линии называются направляющими (m).
Образование поверхностей
1. Аналитический. Характеризует задание непрерывной поверхности. В этом случае поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют уравнению, задающему поверхность: F = (x, y, z) = 0
2. Каркасный. Берется плотный каркас линий, принадлежащих поверхности.
3. Кинематический.(Используется в инженерной графике).
Кинематический. В этом случае поверхность рассматривается как совокупность последовательных положений некоторой линии, называемой образующей l, непрерывно перемещающейся в пространстве вдоль другой линии – направляющей q – по определённому закону. Такие поверхности называют кинематическими.
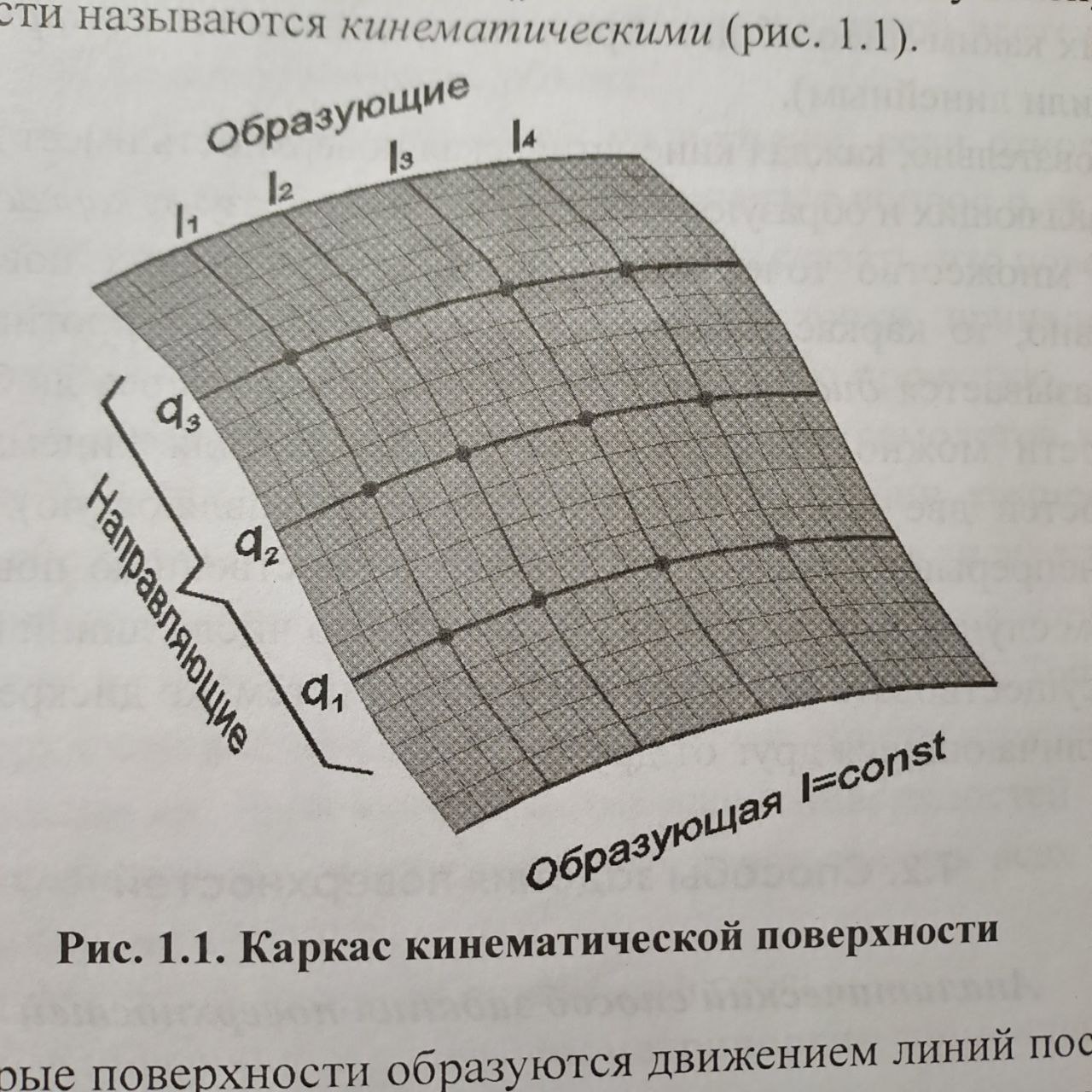
Определитель поверхности - это совокупность условий, однозначно определяющих поверхность в пространстве.
геометрическая часть определителя - изображение образующей и направляющей.
алгоритмическая часть определителя - устанавливает связь между геометрическими элементами.
Множество точек или линий, принадлежащих поверхности и объединённых каким-либо общим признаком, называется её каркасом (точечным или линейным)
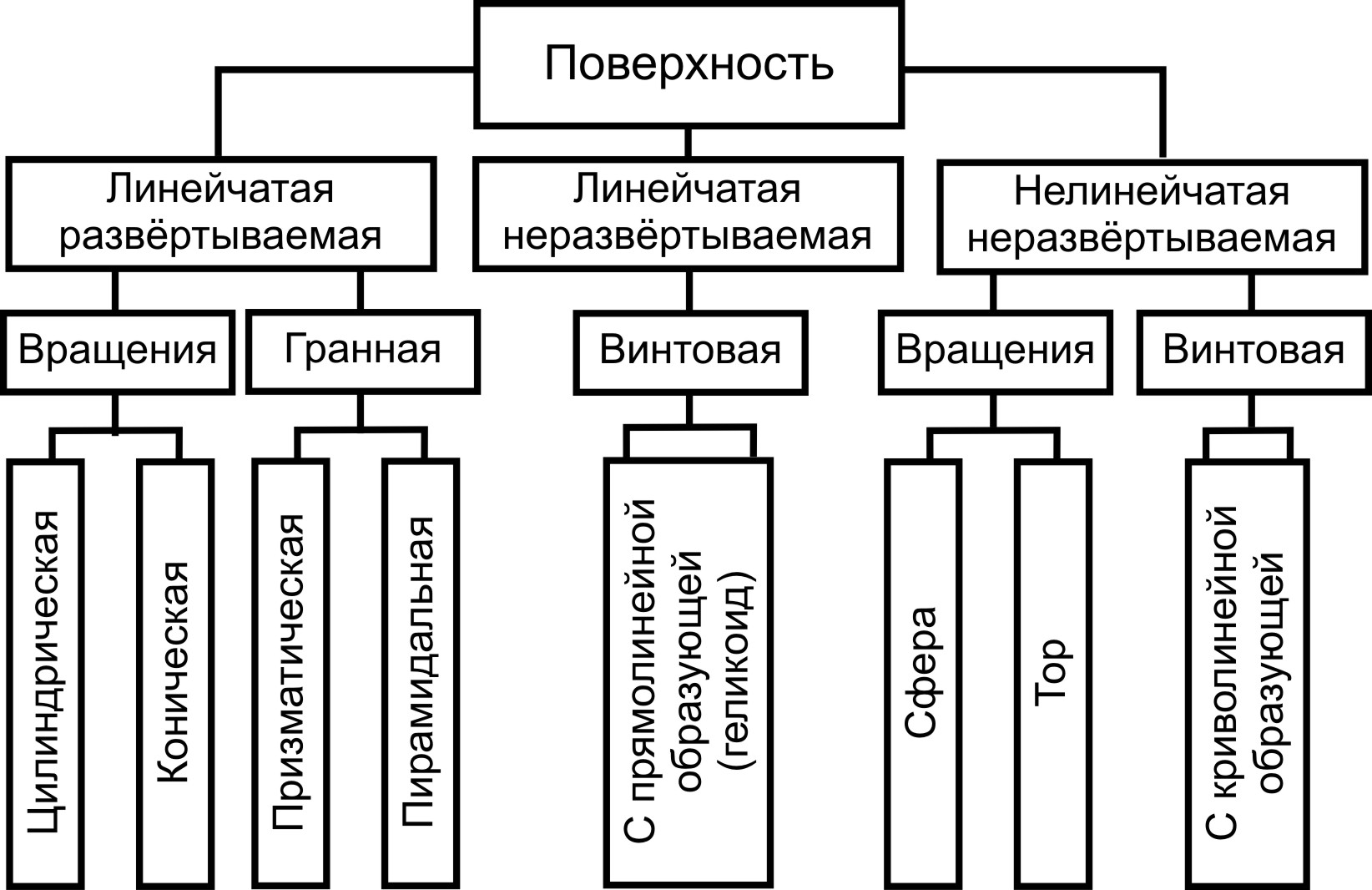
12. Классификация поверхностей.
13. Поверхности вращения. Образование поверхностей вращения.
Поверхности вращения – поверхность, описываемая какой-нибудь линией образующей частности прямой при ее вращении вокруг неподвижной оси.
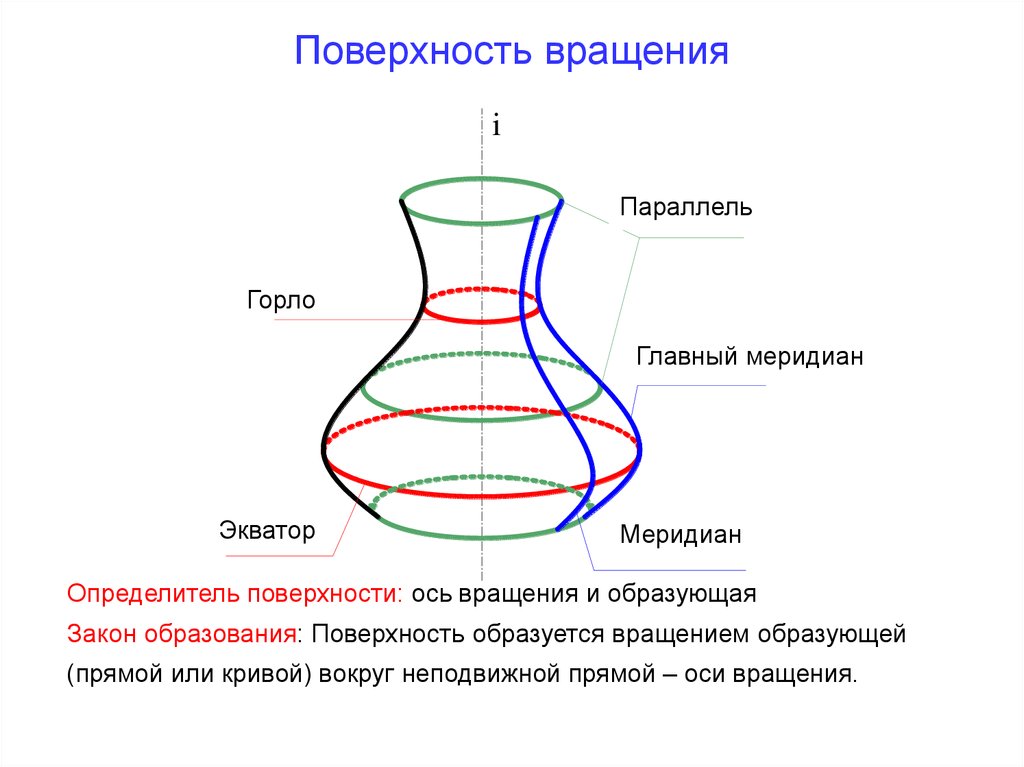
Меридиан, расположенный во фронтальной плоскости проецируется без искажений и называется главным фронтальным меридианом.
Он определяет фронтальный очерк поверхности.
Параллель наибольшего размера называется экватором, наименьшего - горлом.
Экватор определяет горизонтальный очерк поверхности.
Линейчатая поверхность:
Цилиндр и конус - образующая прямая линия
Нелинейчатая поверхность:
Сферическая и торовая поверхность - образующая окружность.
Цилиндр - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными основаниями (плоскостями).
Конус - геометрическое тело, ограниченное конической поверхностью, которая получается при вращении прямой, закрепленной на оси, и плоскостью, пересекающей все образующие.
Если ось конуса перпендикулярна основаниям, такой конус называется прямым.
14. Плоские сечения конуса.
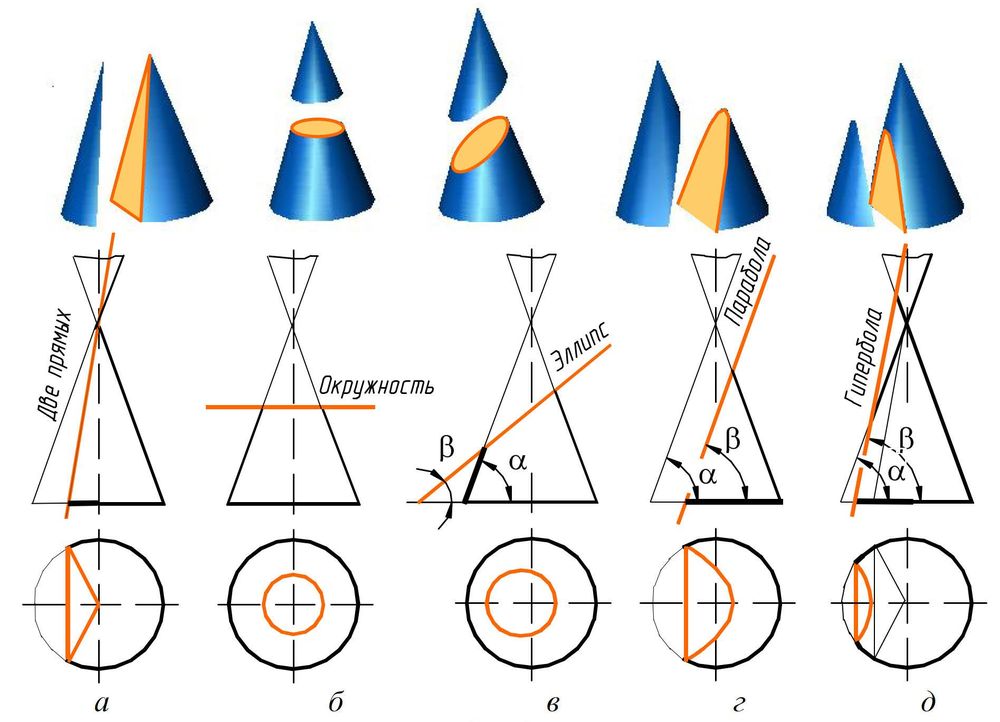
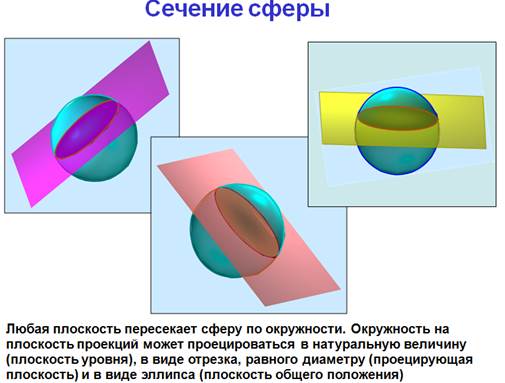
15. Основные каркасные линии сферы. Плоские сечения сферы.
Сфера - поверхность, образованная вращением окрестности вокруг отрезка, являющегося ее диаметром.
Экватор - окружность, которая получается пересечением сферы плоскостью перпендикулярной оси вращения и проходящей через центр сферы.
Меридиан - окружность, которая получается пересечением сферы плоскостью перпендикулярной плоскости экватора и проходящей через центр сферы.
16. Определение линии пересечения двух геометрических тел (частный случай).
Частный случай пересечения:
-
Если одна из поверхностей занимает проецирующее положение, то её вырожденная проекция (своя поверхность, спроецированная в линию), включая проекцию линии пересечения -
Вторая проекция этой линии строится из условия принадлежности её точек не проецирующей поверхности (при помощи линии каркаса) -
А третья – по координатам ОСК
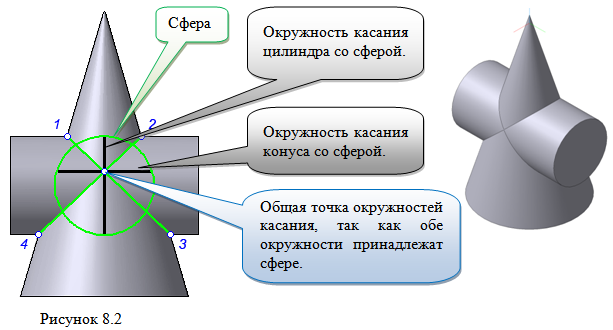
Теорема Монжа 1. Две поверхности, описанные вокруг общей сферы, пересекаются по двум плоским кривым (Рисунок 8.1).
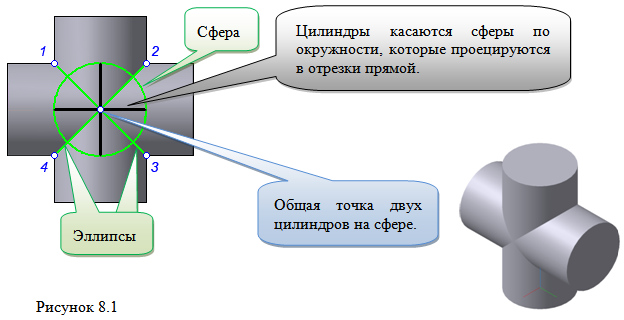
Крайние образующие цилиндров пересекаются в точках 1, 2, 3, 4.
Цилиндры пересекаются по эллипсам.
