Файл: Методы оптимизации.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчеты по практике

Дисциплина: Не указана

Добавлен: 28.04.2024

Просмотров: 26

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

1 Введение

2. Ход работы

Минимизация одномерной функции f2(x)

Минимизация многомерной функции без ограничений на переменные

Минимизация многомерной функции без ограничений на переменные



Весь код для минимизации многомерной функции без ограничений на переменные находится в приложении Б и В.

В качестве условия остановки было выбрано значение равное 0.001.


      1. Минимизация многомерной функции f1(x)



Функция f1(x) задана формулой f1(x) = 2*(X1 - 7) * (X1 - 7) + 5 * (X2 - 2) * (X2 - 2)

График функции представлен на рисунке 2.1. Исходя из графика можно увидеть, что точка минимума находится по координатам (7;2).



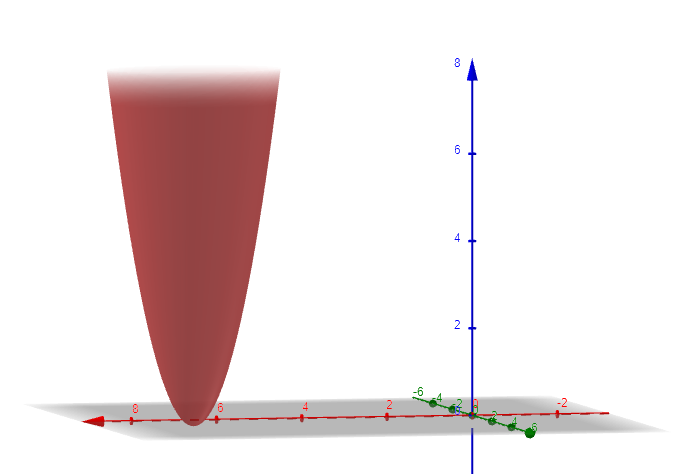
Рисунок 2.2 – График многомерной функции f1(x)




На рисунке 2.3-2.7 представлен результат работы программы для

f1(x) функции

Для каждого метода начальная точка бралась с координатами (0;0). Метод

быстрого спуска сошёлся за 11 итераций, метод Гельфанда-Цейтлина сошёлся сразу же, не зависимо от выбранной точки. Метод Нелдера-Мида работал 5 итераций.




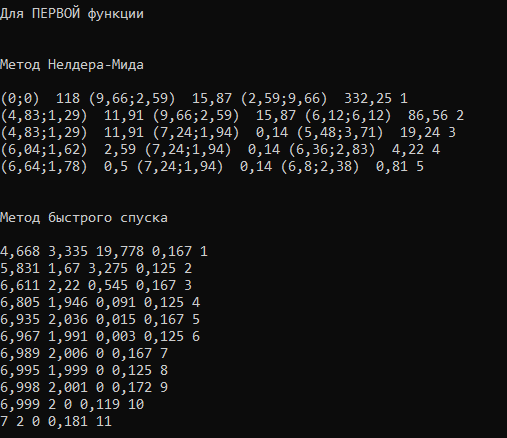
Рисунок 2.3 – Работа программы для функции f1(x) методами Нелдера-Мида и быстрого спуска


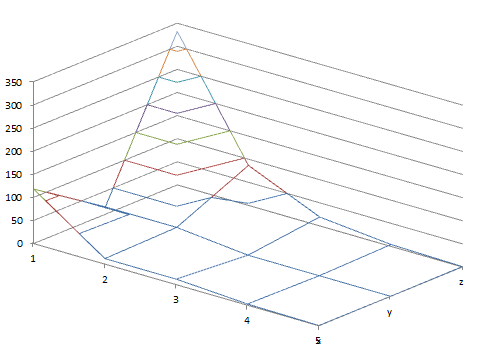
Рисунок 2.4 – График программы для функции f1(x) методом Нелдера-Мида



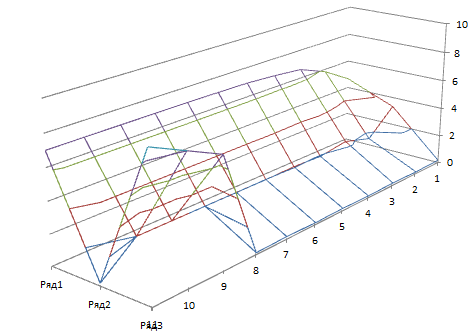
Рисунок 2.5 – График программы для
функции f1(x) методом быстрого спуска


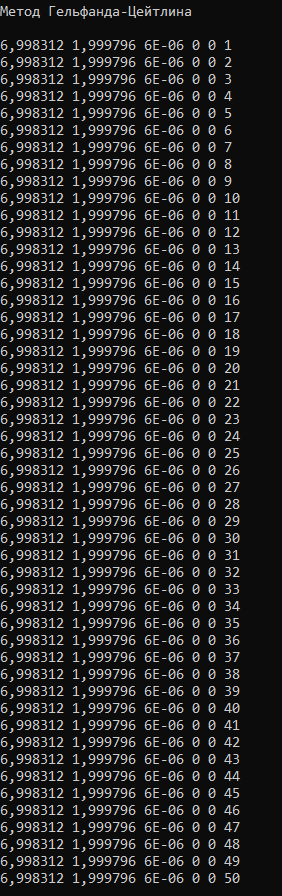
Рисунок 2.6 – Работа программы для функции f1(x) методом Гельфанда-Цейтлина



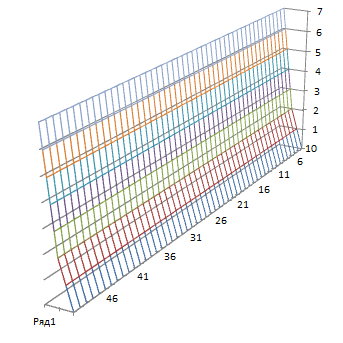
Рисунок 2.7 – График программы для функции f1(x) методом Гельфанда-Цейтлина


      1. Минимизация многомерной функции f2(x)



Функция f2(x) задана формулой f2(x) = (X1 - 2) * (X1 - 2) + (X2 - 7) * (X2 - 7) + 50 * (X2 + 2 * X1 - 6) * (X2 + 2 * X1 - 6) + 7.6

График функции представлен на рисунке 2.8. Исходя из графика можно увидеть, что точка минимума находится по координатам (0,009;6,01).



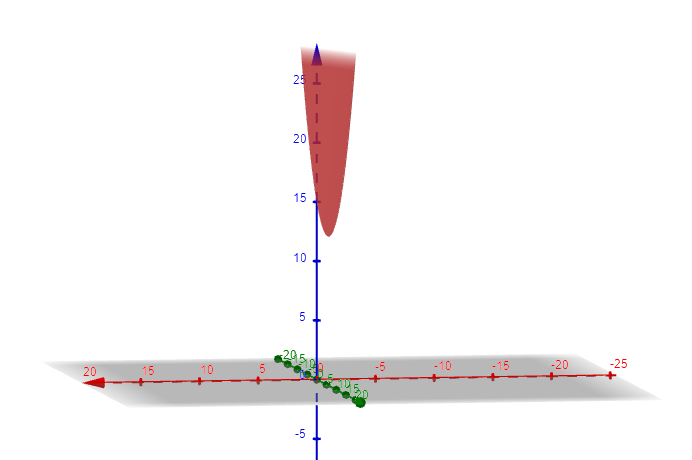
Рисунок 2.8 – График многомерной функции f2(x)

Для каждого метода начальная точка бралась с координатами (0;0). Метод быстрого спуска сошёлся за 568 итераций, метод Гельфанда-Цейтлина сошёлся за 30 итераций. Метод Нелдера-Мида работал 17 итераций.

На рисунке 2.9-2.15 представлен результат работы программы для функции

f2(x).



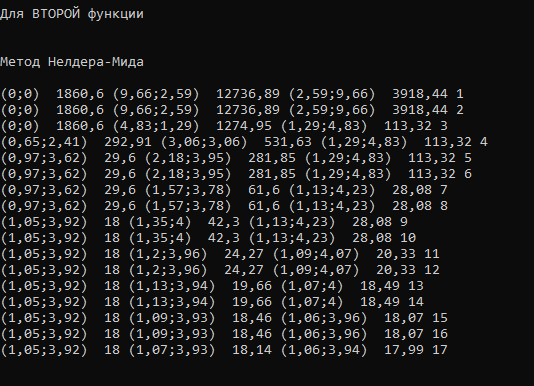
Рисунок 2.9– Работа программы для функции f2(x) методом Нелдера-Мида


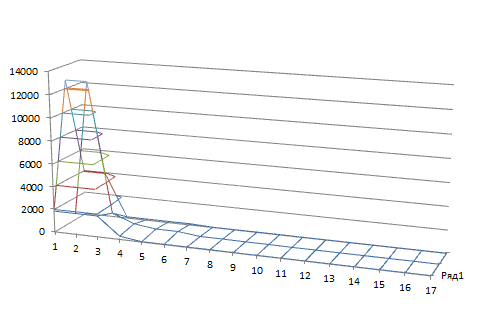
Рисунок 2.10 – График программы для функции f2(x) методом Нелдера-Мида



Рисунок 2.11 – Работа программы для
функции f2(x) методом Быстрого спуска первые 15 итераций


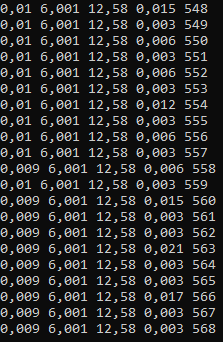
Рисунок 2.12 – Работа программы для функции f2(x) методом Быстрого спуска последние 20 итераций



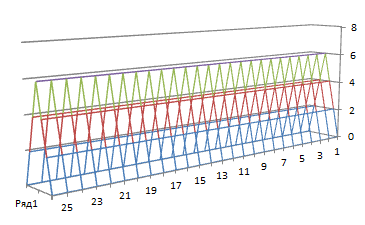
Рисунок 2.13 – График программы для функции f2(x) методом Быстрого спуска последние 20 итераций


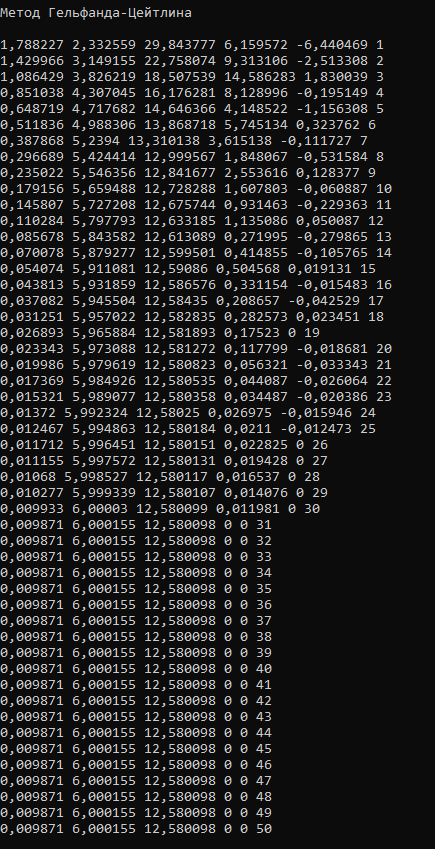
Рисунок 2.14 – Работа программы для функции f2(x) методом Гельфанда-Цейтлина



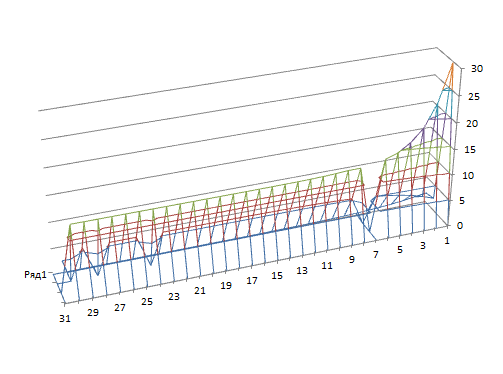Рисунок 2.15 – График программы для функции f2(x) методом Гельфанда-Цейтлина



3 Заключение


В ходе выполнения лабораторной работы мы ознакомились с методами минимизации одномерных и многомерных функций.





Приложение А
(обязательное)

using System;
namespace Lab1_1

{

internal class Program

{

static void Main(string[] args)

{

int N = 0;

double A = 0;

double Y = 0;

List xf1 = new List();

List xf2 = new List();

List xf3 = new List();

List yf1 = new List();

List yf2 = new List();

List yf3 = new List();
Console.WriteLine("ЗОЛОТОЕ СЕЧЕНИЕ");
Console.WriteLine("\nПервая функция");

GoldenRatio(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf1.Clear(); yf1.Clear();

Console.WriteLine("\nВторая функция");

GoldenRatio(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf1.Clear(); yf1.Clear();

Console.WriteLine("\nТретья функция");

GoldenRatio(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf1, ref yf1);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf1.Clear(); yf1.Clear();
Console.WriteLine("МЕТОД ДИХОТОМИИ");
Console.WriteLine("\nПервая функция");

DihMeth(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf2.Clear(); yf2.Clear();

Console.WriteLine("\nВторая функция");

DihMeth(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf2.Clear(); yf2.Clear();

Console.WriteLine("\nТретья функция");

DihMeth(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf2, ref yf2);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf2.Clear(); yf2.Clear();
Console.WriteLine("МЕТОД ФИБОНАЧЧИ");
FibonachiMethod(FirstFunction(), 0, 10, ref N, ref A, ref Y, ref xf3, ref yf3);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf3.Clear(); yf3.Clear();

Console.WriteLine("\nВторая функция");

FibonachiMethod(SecondFunction(), 0, 10, ref N, ref A, ref Y, ref xf3, ref yf3);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

A = Y = 0; N = 0;

xf3.Clear(); yf3.Clear();

Console.WriteLine("\nТретья функция");

FibonachiMethod(ThirdFunction(), 0, 10, ref N, ref A, ref Y, ref xf3, ref yf3);

Console.Write($"Входная точка: {A}, Минимальное значение функции = {Y} Число итераций: {N}\n");

xf3.Clear(); yf3.Clear();

}
static Operation FirstFunction()

{
double GetFunction(double x)

{

return 2 * (x - 7) * (x - 5) * (x - 2);

}
return GetFunction;

}
static Operation SecondFunction()

{

double GetFunction(double x)

{

return x / 2 + 7 * Math.Sin(5 * 3.14 * x + 2);

}

return GetFunction;

}
static Operation ThirdFunction()

{

double GetFunction(double x)

{

return 2 - 7 * Math.Exp(-1 * Math.Pow((x - 5) / 2, 2));

}

return GetFunction;

}
static (double, double, int) GoldenRatio(Operation Function, double a, double b, ref int N, ref double A, ref double Y, ref List xf1, ref List yf1)

{

double XB, XA;

const double Alph = 0.618;

const double Bet = 0.382;
while (Math.Abs(a - b) > 0.0001)

{

XB = a + Bet * Math.Abs(a - b);

XA = a + Alph * Math.Abs(a - b);

if (Function(XB) > Function(XA))

{

a = XB;
}

else

{

b = XA;

}

N++;

if (Function(a) < Function(b))

{

A = a;

xf1.Add(a);

Y = Function(a);

yf1.Add(Y);

}

else

{

A = b;

xf1.Add(a);

Y = Function(b);

yf1.Add(Y);

}

Console.WriteLine("{0}\t{1:F5}\t{2:F5}", N, A, Y);

}
if (Function(a) < Function(b))

{

A = a;

Y = Function(a);

return (A, Y, N);

}

else

{

A = b;

Y = Function(b);

return (A, Y, N);

}

}
static (double, double, int) DihMeth(Operation Function, double a, double b, ref int N, ref double A, ref double Y, ref List xf2, ref List yf2)

{

double Sigma = 0.00001;

double X1;

double X2;

while (Math.Abs(a - b) >= 0.0001)

{

X1 = (a + b - Sigma) / 2;

X2 = (a + b + Sigma) / 2;

if (Function(X1) > Function(X2))

{

a = X1;

}

else

{

b = X1;

}

N++;

A = (a + b) / 2;

xf2.Add(A);

Y = Function(a);

yf2.Add(Y);

Console.WriteLine("{0}\t{1:F5}\t{2:F5}", N, A, Y);

}

A = (a + b) / 2;

Y = Function(a);

return (A, Y, N);

}

static (double, double, int) FibonachiMethod(Operation Function, double a, double b, ref int N, ref double A, ref double Y, ref List xf3, ref List yf3)

{

double X1, X2;

int k, n = 0;

k = 1;

long usl = Convert.ToInt64(NumberFib(1));
for (int i = 1; usl < (Math.Abs(a - b) / 0.0001); i++, n = i - 1)

usl = Convert.ToInt64(NumberFib(i));

while (Math.Abs(a - b) >= 0.0001)

{

X1 = a + (NumberFib(n - k + 1) / NumberFib(n - k + 3) * (b - a));

X2 = a + (NumberFib(n - k + 2) / NumberFib(n - k + 3) * (b - a));

if (Function(X1) >= Function(X2))

{

a = X1;

k++;

}

else

{

b = X2;

k++;

}

N++;

A = (a + b) / 2;

xf3.Add(A);

Y = Function((a + b) / 2);

yf3.Add(Y);

Console.WriteLine("{0}\t{1:F5}\t{2:F5}", N, A, Y);

}

A = (a + b) / 2;

Y = Function((a + b) / 2);

return (A, Y, N);

}
static double NumberFib(int num)

{

return Convert.ToInt64((Math.Pow((1 + Math.Sqrt(5)) / 2, num) - Math.Pow((1 - Math.Sqrt(5)) / 2, num)) / Math.Sqrt(5));

}
delegate double Operation(double g);

delegate int Operati(int n);

}

}
Приложение Б
(обязательное)


namespace MO21

{

public class Program

{

public static double D(double a, double b)

{

return b - a;

}

private static double DeFfirst(double X1, double X2)

{

return 4 * X1 - 28;

}

private static double DeFsecond(double X1, double X2)

{

return 10 * X2 - 20;

}

private static double Function(double X1, double X2)

{

return 2 * (X1 - 7) * (X1 - 7) + 5 * (X2 - 2) * (X2 - 2);

}

private static void FastDown()

{

double X11 = 0;

double X12 = 0;

double epsilon = 0.001;

double border_a = -2000;

double border_b = 2000;

double Alfa = 0.618;

double Beta = 0.382;

int count = 0;

do

{

double t = Gold(border_a, border_b, Alfa, Beta, X11, X12);

double tempX1 = X11;

double tempX2 = X12;

X11 = X11 - t * DeFfirst(tempX1, tempX2);

X12 = X12 - t * DeFsecond(tempX1, tempX2);

count++;

Console.WriteLine(Math.Round(X11, 3) + " " + Math.Round(X12, 3) + " " + Math.Round(Function(X11, X12), 3) + " " + Math.Round(t, 3) + " " + count);

} while (Math.Abs(DeFfirst(X11, X12)) > epsilon && Math.Abs(DeFsecond(X11,

X12)) > epsilon);

}

private static void GelfCeit()

{

double t1, t2, X01 = 0, X02 = 0, GlobalCount = 0, Count1 = 0, Count2 = 0,

G1, G2, Alf = 0.618, Bet = 1 - Alf;

do

{

do

{

if (Math.Abs(DeFfirst(X01, X02)) > 0.01)

{

G1 = DeFfirst(X01, X02);

}

else

G1 = 0;

if (Math.Abs(DeFsecond(X01, X02)) > 0.01)

{

G2 = DeFsecond(X01, X02);

}

else

G2 = 0;

t1 = Gold(-2000, 2000, Alf, Bet, X01, X02);

X01 -= t1 * G1;

X02 -= t1 * G2;

Count1++;

} while (Count1 < 10);

Count1 = 0;

do

{

if (Math.Abs(DeFfirst(X01, X02)) > 0.01)

{

G1 = DeFfirst(X01, X02);

}

else

G1 = 0;

if (Math.Abs(DeFsecond(X01, X02)) > 0.01)

{

G2 = DeFsecond(X01, X02);

}

else

G2 = 0;

t2 = Gold(-2000, 2000, Alf, Bet, X01, X02);

X01 -= t2 * G1;

X02 -= t2 * G2;

Count2++;

} while (Count2 < 10);

Count2 = 0;

GlobalCount++;

Console.WriteLine(Math.Round(X01, 6) + " " + Math.Round(X02, 6) + " "

+ Math.Round(Function(X01, X02), 6) + " " + Math.Round(G1, 6) + " " + Math.Round(G2,

6) + " " + GlobalCount);

} while (GlobalCount < 50);

}

public static double Gold(double a, double b, double Alf, double Bet, double

X11, double X12)

{

var count = 0;

double XB;

double XA;

do

{

XB = a + Bet * D(a, b);

XA = a + Alf * D(a, b);

if (T(X11, X12, XB) >= T(X11, X12, XA))

{

a = XB;

}

else

{

b = XA;

}

count++;

} while (D(a, b) >= 0.01);

if (T(X11, X12, XA) <= T(X11, X12, XB))

{

return XA;

}

else

{

return XB;

}

}

private static void Main(string[] args)

{

Console.WriteLine("\nДля ПЕРВОЙ функции\n");

Console.WriteLine("\nМетод Нелдера-Мида\n");

NelderMid();

Console.WriteLine("\nМетод быстрого спуска\n");

FastDown();

Console.WriteLine("\nМетод Гельфанда-Цейтлина\n");

GelfCeit();

}

private static void NelderMid()

{

var n = 2;

var count = 1;

double Xh = 0, Xh1, Xh2, Xl = 0, Xl1, Xl2, t = 10, X11, X12, X21, X22,

X31, X32, X61, X62, X71, X72, A, X51, X52, X41, X42, Max, Min;

var d2 = t * (Math.Pow(n + 1, 0.5) - 1) / (Math.Pow(2, 0.5) * n);

var d1 = t * (Math.Pow(n + 1, 0.5) + n - 1) / (Math.Pow(2, 0.5) * n);

X11 = 0;

X12 = 0;

X21 = d1;

X22 = d2;

X31 = d2;

X32 = d1;

Max = double.MinValue;

Min = double.MaxValue;

if (Function(X11, X12) > Function(X21, X22) && Function(X11, X12) >

Function(X31, X32))

{

Xh = Function(X11, X12);

Xh1 = X11;

Xh2 = X12;

}

else if (Function(X21, X22) > Function(X11, X12) && Function(X21, X22) >

Function(X31, X32))

{

Xh = Function(X21, X22);

Xh1 = X21;

Xh2 = X22;

}

else

{

Xh = Function(X31, X32);

Xh1 = X31;

Xh2 = X32;

}

if (Function(X11, X12) < Function(X21, X22) && Function(X11, X12) <

Function(X31, X32))

{

Xl = Function(X11, X12);

Xl1 = X11;

Xl2 = X12;

}

else if (Function(X21, X22) < Function(X11, X12) && Function(X21, X22) <

Function(X31, X32))

{

Xl = Function(X21, X22);

Xl1 = X21;

Xl2 = X22;

}

else

{

Xl = Function(X31, X32);

Xl1 = X31;

Xl2 = X32;

}

do

{

Console.Write("(" + Math.Round(X11, 2) + ";" + Math.Round(X12, 2) + ") " + Math.Round(Function(X11, X12), 2) + " ");
Console.Write("(" + Math.Round(X21, 2) + ";" + Math.Round(X22, 2) + ") " + Math.Round(Function(X21, X22), 2) + " ");
Console.Write("(" + Math.Round(X31, 2) + ";" + Math.Round(X32, 2) + ") " + Math.Round(Function(X31, X32), 2) + " ");
Console.WriteLine(count);

//смещенный центр тяжести

if (Xh == Function(X11, X12))

{

X41 = (X21 + X31) / n;

X42 = (X22 + X32) / n;

}

else if (Xh == Function(X21, X22))

{

X41 = (X11 + X31) / n;

X42 = (X12 + X32) / n;

}

else

{

X41 = (X11 + X21) / n;

X42 = (X12 + X22) / n;

}

//точка отражения

X51 = 2 * X41 - Xh1;

X52 = 2 * X42 - Xh2;

if (Function(X51, X52) < Xl)

{

//точка растяжения

X61 = 2 * X51 - X41;

X62 = 2 * X52 - X42;

if (Function(X61, X62) < Xl)

{

Xh1 = X61;

Xh2 = X62;

Xh = Function(Xh1, Xh2);

}

else

{

Xh1 = X51;

Xh2 = X52;

Xh = Function(Xh1, Xh2);

}

}

else

{

if (Function(X51, X52) > Function(X11, X12) && Function(X51, X52)

> Function(X21, X22) && Function(X51, X52) > Function(X31, X32))

{

if (Function(X51, X52) > Xh)

{

//редукция

X11 = 0.5 * Xl1 + 0.5 * X11;

X12 = 0.5 * Xl2 + 0.5 * X12;

X21 = 0.5 * Xl1 + 0.5 * X21;

X22 = 0.5 * Xl2 + 0.5 * X22;

X31 = 0.5 * Xl1 + 0.5 * X31;

X32 = 0.5 * Xl2 + 0.5 * X32;

if (Function(X11, X12) > Function(X21, X22) &&

Function(X11, X12) > Function(X31, X32) && Function(X11, X12) > Max)

{

Xh = Function(X11, X12);

Xh1 = X11;

Xh2 = X12;

}

else if (Function(X21, X22) > Function(X11, X12) &&

Function(X21, X22) > Function(X31, X32) && Function(X21, X22) > Max)

{

Xh = Function(X21, X22);

Xh1 = X21;

Xh2 = X22;

}

else

{

Xh = Function(X31, X32);

Xh1 = X31;

Xh2 = X32;

}

if (Function(X11, X12) < Function(X21, X22) &&

Function(X11, X12) < Function(X31, X32) && Function(X11, X12) < Min)

{

Xl = Function(X11, X12);

Xl1 = X11;

Xl2 = X12;

}

else if (Function(X21, X22) < Function(X11, X12) &&

Function(X21, X22) < Function(X31, X32) && Function(X21, X22) < Min)

{

Xl = Function(X21, X22);

Xl1 = X21;

Xl2 = X22;

}

else

{

Xl = Function(X31, X32);

Xl1 = X31;

Xl2 = X32;

}

}

else

{

//Сжатие

X71 = 0.5 * X51 - X41;

X72 = 0.5 * X52 - X42;

if (Function(X71, X72) > Xh)

{

//редукция

X11 = 0.5 * Xl1 + 0.5 * X11;

X12 = 0.5 * Xl2 + 0.5 * X12;

X21 = 0.5 * Xl1 + 0.5 * X21;

X22 = 0.5 * Xl2 + 0.5 * X22;

X31 = 0.5 * Xl1 + 0.5 * X31;

X32 = 0.5 * Xl2 + 0.5 * X32;

if (Function(X11, X12) > Function(X21, X22) &&

Function(X11, X12) > Function(X31, X32) && Function(X11, X12) > Max)

{

Xh = Function(X11, X12);

Xh1 = X11;

Xh2 = X12;

}

else if (Function(X21, X22) > Function(X11, X12) &&

Function(X21, X22) > Function(X31, X32) && Function(X21, X22) > Max)

{

Xh = Function(X21, X22);

Xh1 = X21;

Xh2 = X22;

}

else

{

Xh = Function(X31, X32);

Xh1 = X31;

Xh2 = X32;

}

if (Function(X11, X12) < Function(X21, X22) &&

Function(X11, X12) < Function(X31, X32) && Function(X11, X12) < Min)

{

Xl = Function(X11, X12);

Xl1 = X11;

Xl2 = X12;

}

else if (Function(X21, X22) < Function(X11, X12) &&

Function(X21, X22) < Function(X31, X32) && Function(X21, X22) < Min)

{

Xl = Function(X21, X22);

Xl1 = X21;

Xl2 = X22;

}

else

{

Xl = Function(X31, X32);

Xl1 = X31;

Xl2 = X32;

}

}

else

{

Xh1 = X71;

Xh2 = X72;

Xh = Function(Xh1, Xh2);

}

}

}

else

{

Xh1 = X51;

Xh2 = X52;

Xh = Function(Xh1, Xh2);

}

}

count++;

A = (Math.Pow(Function(X11, X12) - Function(X41, X42), 2) +

Math.Pow(Function(X21, X22) - Function(X41, X42), 2) + Math.Pow(Function(X31, X32) -

Function(X41, X42), 2)) / (n + 1);

} while (A >= 0.01);

Console.WriteLine();

}

public static double T(double X11, double X12, double t)

{

return 2*((X11 - t * DeFfirst(X11, X12)) - 7) * ((X11 - t * DeFfirst(X11, X12)) -7) +5 * ((X12 - t * DeFsecond(X11, X12)) - 2) * ((X12 - t * DeFsecond(X11,X12)) - 2);

}

}

}

Приложение В
(обязательное)

namespace MO22

{

public class Program

{

public static double D(double a, double b)

{

return b - a;

}

private static double DeFfirst(double X1, double X2)

{

return 402 * X1 + 200 * X2 - 1204;

}

private static double DeFsecond(double X1, double X2)

{

return 200 * X1 + 102 * X2 - 614;

}

private static double Function(double X1, double X2)

{

return (X1 - 2) * (X1 - 2) + (X2 - 7) * (X2 - 7) + 50 * (X2 + 2 * X1 - 6) * (X2 + 2 * X1 - 6) + 7.6;

}

private static void FastDown()

{

double X11 = 0;

double X12 = 0;

double epsilon = 0.001;

double border_a = -2000;

double border_b = 2000;

double Alfa = 0.618;

double Beta = 0.382;

int count = 0;

do

{

double t = Gold(border_a, border_b, Alfa, Beta, X11, X12);

double tempX1 = X11;

double tempX2 = X12;

X11 = X11 - t * DeFfirst(tempX1, tempX2);

X12 = X12 - t * DeFsecond(tempX1, tempX2);

count++;

Console.WriteLine(Math.Round(X11, 3) + " " + Math.Round(X12, 3) + " "

+ Math.Round(Function(X11, X12), 3) + " " + Math.Round(t, 3) + " " + count);

} while (Math.Abs(DeFfirst(X11, X12)) > epsilon && Math.Abs(DeFsecond(X11,

X12)) > epsilon);

}

private static void GelfCeit()

{

double t1, t2, X01 = 0, X02 = 0, GlobalCount = 0, Count1 = 0, Count2 = 0,

G1, G2, Alf = 0.618, Bet = 1 - Alf;

do

{

do

{

if (Math.Abs(DeFfirst(X01, X02)) > 0.01)

{

G1 = DeFfirst(X01, X02);

}

else

G1 = 0;

if (Math.Abs(DeFsecond(X01, X02)) > 0.01)

{

G2 = DeFsecond(X01, X02);

}

else

G2 = 0;

t1 = Gold(-2000, 2000, Alf, Bet, X01, X02);

X01 -= t1 * G1;

X02 -= t1 * G2;

Count1++;

} while (Count1 < 10);

Count1 = 0;

do

{

if (Math.Abs(DeFfirst(X01, X02)) > 0.01)

{

G1 = DeFfirst(X01, X02);

}

else

G1 = 0;

if (Math.Abs(DeFsecond(X01, X02)) > 0.01)

{

G2 = DeFsecond(X01, X02);

}

else

G2 = 0;

t2 = Gold(-2000, 2000, Alf, Bet, X01, X02);

X01 -= t2 * G1;

X02 -= t2 * G2;

Count2++;

} while (Count2 < 10);

Count2 = 0;

GlobalCount++;

Console.WriteLine(Math.Round(X01, 6) + " " + Math.Round(X02, 6) + " "

+ Math.Round(Function(X01, X02), 6) + " " + Math.Round(G1, 6) + " " + Math.Round(G2,

6) + " " + GlobalCount);

} while (GlobalCount < 50);

}

public static double Gold(double a, double b, double Alf, double Bet, double

X11, double X12)

{

var count = 0;

double XB;

double XA;

do

{

XB = a + Bet * D(a, b);

XA = a + Alf * D(a, b);

if (T(X11, X12, XB) >= T(X11, X12, XA))

{

a = XB;

}

else

{

b = XA;

}

count++;

} while (D(a, b) >= 0.01);

if (T(X11, X12, XA) <= T(X11, X12, XB))

{

return XA;

}

else

{

return XB;

}

}

private static void Main(string[] args)

{

Console.WriteLine("\nДля ВТОРОЙ функции\n");

Console.WriteLine("\nМетод Нелдера-Мида\n");

NelderMid();

Console.WriteLine("\nМетод быстрого спуска\n");

FastDown();

Console.WriteLine("\nМетод Гельфанда-Цейтлина\n");

GelfCeit();
}

private static void NelderMid()

{

var n = 2;

var count = 1;

double Xh = 0, Xh1, Xh2, Xl = 0, Xl1, Xl2, t = 10, X11, X12, X21, X22,

X31, X32, X61, X62, X71, X72, A, X51, X52, X41, X42, Max, Min;

var d2 = t * (Math.Pow(n + 1, 0.5) - 1) / (Math.Pow(2, 0.5) * n);

var d1 = t * (Math.Pow(n + 1, 0.5) + n - 1) / (Math.Pow(2, 0.5) * n);

X11 = 0;

X12 = 0;

X21 = d1;

X22 = d2;

X31 = d2;

X32 = d1;

Max = double.MinValue;

Min = double.MaxValue;

if (Function(X11, X12) > Function(X21, X22) && Function(X11, X12) >

Function(X31, X32))

Смотрите также файлы