Файл: Содержание Теоретический раздел 4.doc

Переходим к основному алгоритму симплекс-метода.

№1

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В индексной строке F(x) выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее:

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (5) и находится на пересечении ведущего столбца и ведущей строки.

Базис	В	x1	x2	x3	x4	x5	min
x3	432	2	5	1	0	0	86.4
x4	424	3	4	0	1	0	106
x5	532	5	3	0	0	1	177.33
F(X1)	0	-34	-50	0	0	0	0

После преобразований получаем новую таблицу:

Базис	В	x1	x2	x3	x4	x5
x2	86.4	0.4	1	0.2	0	0
x4	78.4	1.4	0	-0.8	1	0
x5	272.8	3.8	0	-0.6	0	1
F(X1)	4320	-14	0	10	0	0

---

№2

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В индексной строке F(x) выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i1

и из них выберем наименьшее:

Следовательно, 2-ая строка является ведущей.

Разрешающий элемент равен (1.4) и находится на пересечении ведущего столбца и ведущей строки.

Базис	В	x1	x2	x3	x4	x5	min
x2	86.4	0.4	1	0.2	0	0	216
x4	78.4	1.4	0	-0.8	1	0	56
x5	272.8	3.8	0	-0.6	0	1	71.79
F(X2)	4320	-14	0	10	0	0	0

После преобразований получаем новую таблицу:

Базис	В	x1	x2	x3	x4	x5
x2	64	0	1	0.43	-0.29	0
x1	56	1	0	-0.57	0.71	0
x5	60	0	0	1.57	-2.71	1
F(X2)	5104	0	0	2	10	0

---

Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план

Окончательный вариант симплекс-таблицы:

Базис	В	x1	x2	x3	x4	x5
x2	64	0	1	0.43	-0.29	0
x1	56	1	0	-0.57	0.71	0
x5	60	0	0	1.57	-2.71	1
F(X3)	5104	0	0	2	10	0

Оптимальный план можно записать так:

x₂ = 64

x₁ = 56

x₅ = 60

F(X) = 34*56 + 50*64 = 5104

2 способ – геометрический метод

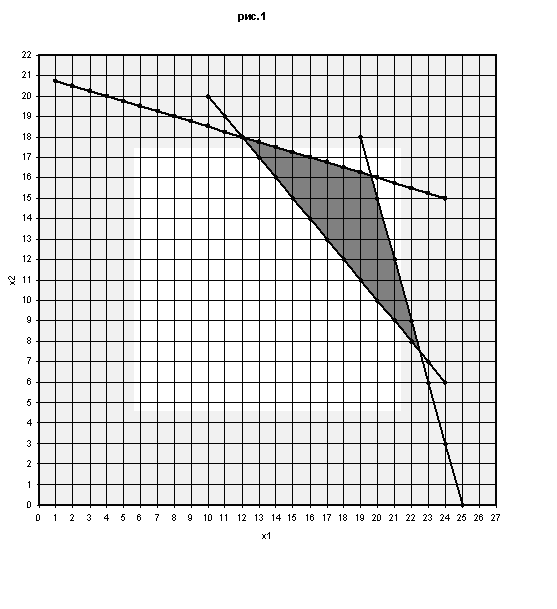
Геометрический метод решения задач оптимизации сводится к нахождению оптимального решения задачи в одной из угловых точек многоугольника(рис. 1) для

линейной функции F = 30х₁ + 40х₂ → max при следующих ограничениях:
3 х₁ + х₂ ≤ 75, (I)

х₁ + х₂ ≤ 30, (II) (12)

х₁ +4х₂ ≤ 84, (III), х₁ ≥ 0, х₂ ≥ 0, х₂ ≥ х₁
по смыслу задачи.

Изобразим многоугольник решений данной задачи.
I

II


О
А

В

С

бласть АВС, изображённая на рисунке, является областью допустимых значений функции F. Принимая во внимание систему (12), можно заметить, что самое оптимальное решение Находится в точке А, находящейся на пересечении прямых I и II, то есть координаты точки А определяются решением системы уравнений:
3 х₁ + х₂ ≤ 75, х₁ = 12,

х₁ + х₂ ≤ 30, или х₂ = 18., т. е. А(12, 18)
максимальное значение линейной функции равно :
F_max= 30*12 + 40*18 = 1080.
Итак, F_max = 1080 при оптимальном решении х₁ = 12, х₂ = 18, т. е. максимальная прибыль в 1080 ден. ед. может быть достигнута при производстве 12 единиц продукции А и 18 единиц продукции В. Ответ: F

---

_max = 1080.

Заключение
Алгоритмы безусловной минимизации(максимизации) функций многих переменных можно сравнивать и исследовать как с теоретической, так и с экспериментальной точек зрения.

Первый подход может быть реализован полностью только для весьма ограниченного класса задач, например, для сильно выпуклых квадратичных функций. При этом возможен широкий спектр результатов от получения бесконечной минимизирующей последовательности в методе циклического покоординатного спуска до сходимости не более чем за n итераций в методе сопряженных направлений.

Мощным инструментом теоретического исследования алгоритмов являются теоремы о сходимости методов. Однако, как правило, формулировки таких теорем абстрактны, при их доказательстве используется аппарат современного функционального анализа. Кроме того, зачастую непросто установить связь полученных математических результатов с практикой вычислений. Дело в том, что условия теорем труднопроверяемы в конкретных задачах, сам факт сходимости мало что дает, а оценки скорости сходимости неточны и неэффективны. При реализации алгоритмов также возникает много дополнительных обстоятельств, строгий учет которых невозможен (ошибки округления, приближенное решение различных вспомогательных задач и т.д.) и которые могут сильно повлиять на ход процесса.

Поэтому на практике часто сравнение алгоритмов проводят с помощью вычислительных экспериментов при решении так называемых специальных тестовых задач. Эти задачи могут быть как с малым, так и с большим числом переменных, иметь различный вид нелинейности. Они могут быть составлены специально и возникать из практических приложений, например задача минимизации суммы квадратов, решение систем нелинейных уравнений и т.п.

Список литературы

1. 
   Трофимов А.А. Информационные системы в экономике и управлении - М.: ЭКОМ, 2007.-227с.
   
2. 
   Попов А.А. Excel: Практическое руководство. М: ДЕСС КОМ, 2000.-356с.
   
3. 
   Козырев А.А. «Информационные системы маркетинга»: методические указания по выполнению контрольной работы для самостоятельной работы студентов» - М.: Вузовский учебник, 2007.-248с.
   
4. 
   Козырев А.А.. Компьютерные информационные технологии в экономике и управлении. - М.: Вузовский учебник, 2007.- 381с.
   
5. 
   Романов А.Н., Одинцов Б.Е. Информационные системы в экономике (лекции, упражнения и задачи): Учеб. пособие. – М.: Вузовский учебник,2007.- 132с.
   

---

---