ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕОБРАЗОВАТЕЛЬНОЕБЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

ФИНАНСОВЫЙ УНИВЕРСИТЕТ

ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ

А ЛТАЙСКИЙ ФИЛИАЛ


По дисциплине «Финансовая математика»

Студент _________________________ Пастухова Алёна Сергеевна

(подпись)

Группа18-1Б-ЭК02 Номер личного дела 100.02/180084

Преподаватель канд.тех.наук, Жевнов Денис Анатольевич

Барнаул 2021



Решение.

По условию задачи

Денежная сумма – разовая, проценты – простые. P=11000, S=12000

Период начисления 8 месяцев.

Формула наращения для простых процентов: 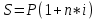, где

S – наращенная сумма в конце срока;

Р – первоначальная сумма;

n – срок ссуды (в годах);

i – процентная ставка.

Выделим из формулы наращения процентную ставку:

i = (S/P-1)*n.

Воспользуемся формулой наращения по простым процентам в MS Excel ( / Дата и время / ДОЛЯ ГОДА). Найдем значение n, учитывая, что вклад на 8 месяцев. В банке используются точные проценты с точным числом дней ссуды (английская практика).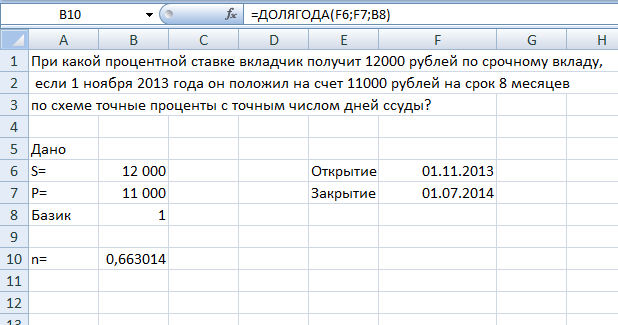



Рис. 1. Расчет доли года.

Теперь определим процентную ставку по формуле i = (S/P-1)*n. Вставим формулу в ячейку В12.



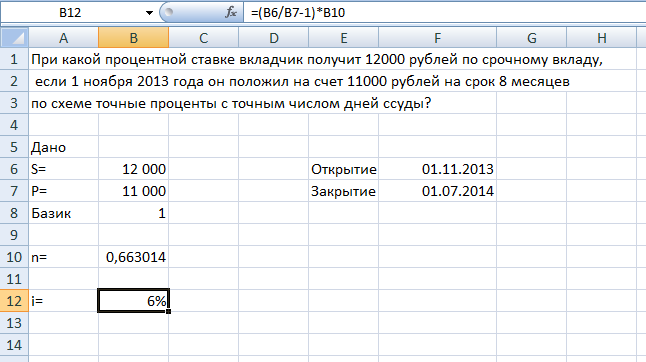
Рис.2. Расчет процентной ставки.
Ответ: процентная ставка 6%.



Решение.

Согласно условию задачи рассматривается операция наращения разовой суммы Р по номинальной процентной ставке j=9,5%. Величина Р не задана, соответствующая наращенная сумма S=100 000.

Срок операции n=2.5 года, m=12(ежемесячное начисление процентов).

Воспользуемся финансовой функцией ПС (Ставка; Кпер; Плт; Бс; Тип).

Расчеты будем производить в MS Excel.

---

Ставка – процентная ставка за период ;

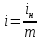Кпер – общее число периодов платежей по аннуитету ;

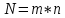Плт – выплата, производимая в каждый период и не меняющаяся на протяжении всего периода ренты;

Бс – требуемое значение будущей стоимости или остатка средств после последней выплаты;


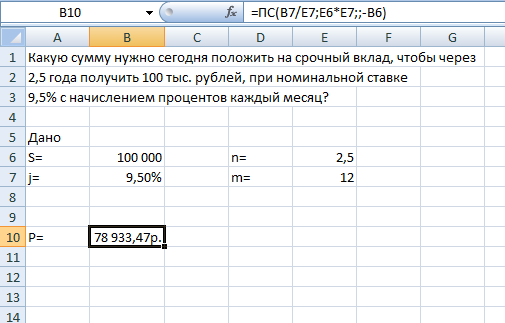
Рис.3. расчет первоначальной суммы вклада
Ответ: сумма которую нужно положить на срочный вклад 78 933,47р.



Решение.

Для нахождения суммы, которую получит векселедержатель будем использовать финансовую функцию ПС (Ставка; Кпер; Плт; Бс; Тип) в Excel.

По условию задачи: S = 60000 рублей, j= 8,6%, n = 1,5, m=2.


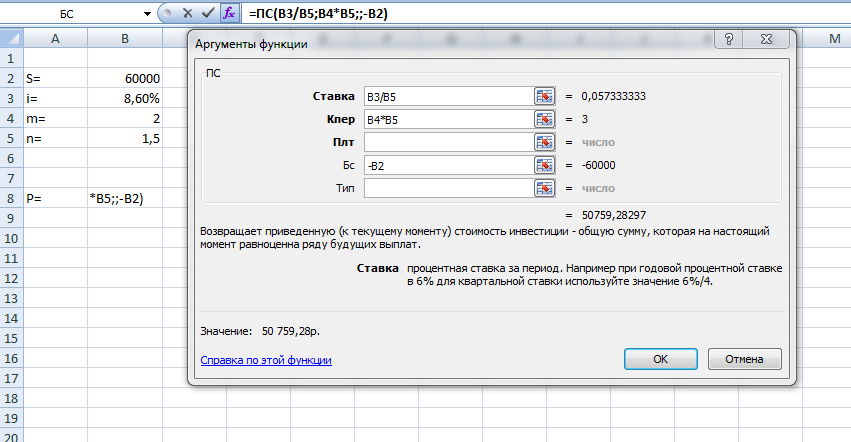
Рис. 3.1. Расчет денежной суммы, которую получит векселедержатель

Ответ: Векселедержатель получит 50 759,28 руб



Решение.

Денежная сумма –переодические платежи:

R=5000

Срок n=15 лет.

Проценты сложные, j=10%, m=12 раз в год.

Для расчета цены, по которой был приобретен станок воспользуемся стандартной финансовой функцией ПС (Ставка; Кпер; Плт; Бс; Тип).



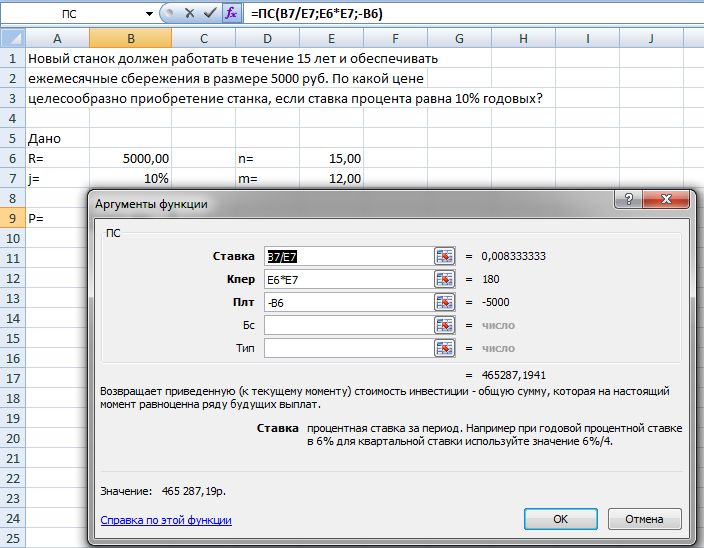
Рис.4 Расчет цены приобритения станка.

Ответ: целесообразно приобрести станок по 465 287,19р.





Решение.

1. 
   Найдем матрицу рисков.
   

Каждый элемент матрицы рисков определяется равенством 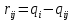, т.е. получается вычитанием данного элемента 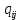из максимального в каждом столбце.

Решение проведем с помощью Excel.

В ячейку В7 введем функцию =МАКС(В3:В6) и скопируем ее в ячейки С7:F7.

---

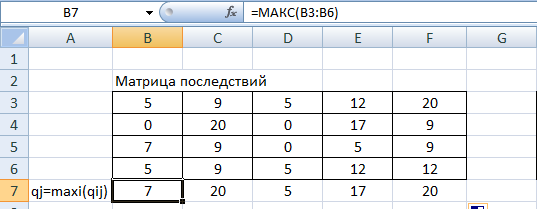
Рис.5. Определение максимального элемента.

Получили: q₁ = 7; q₂ = 20; q₃ = 5; q₄ = 17; q₅ = 20.

Найдем каждый элемент матрицы рисков с помощью равенства



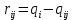
Например, для j-1 получим:









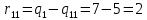
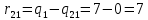
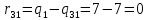
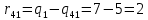
Все вычисления выполним в Excel. Так для элемента r₁₁ в ячейке Н3 будет функция для вычисления =$В7$-В3.

Для элемента r₁₂ в ячейке I3 будет функция =$C7$-C3,

Для элемента r₁₃ в ячейке J3 будет функция =$D7$-D3,

Для элемента r₁₄ в ячейке K3 будет функция =$E7$-E3,

Для элемента r₁₅ в ячейке L3 будет функция =$F7$-F3.

Формулы ячеек H3:L3 скопируем в соответствующие ячейки. И получим матрицу рисков.



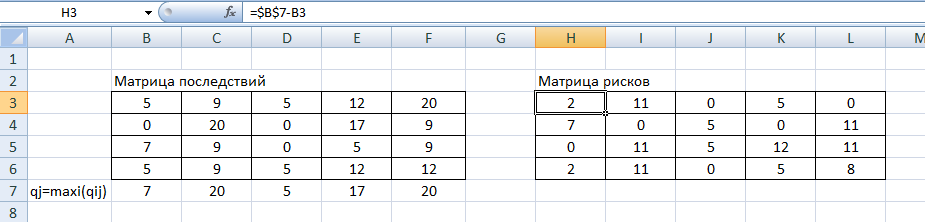
Рис.6. Результаты вычислений.

Матрица рисов имеет вид:

R=

2. 
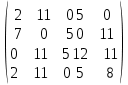
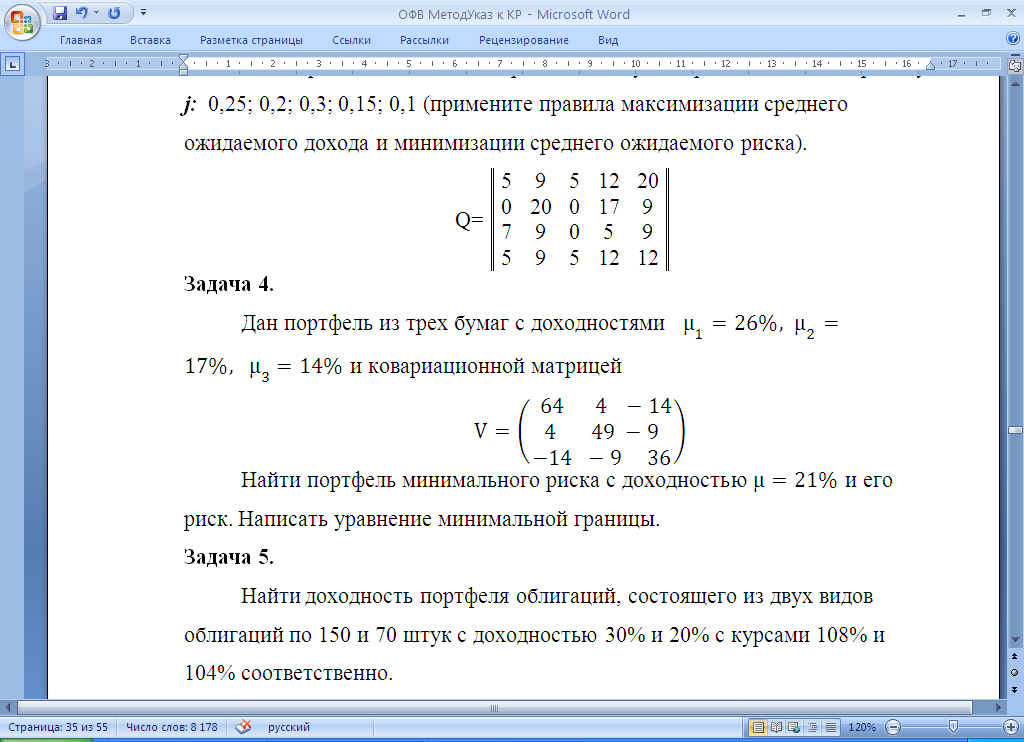
   Проведите анализ ситуации полной неопределенности, применив правила по принятию решений Вальда, Сэвиджа и Гурвица (взять λ равному 0,5; 0,4 и 0,3).
   

Определим решение по правилу Вальда.

Проанализируем каждое решение, т.е в каждой строке матрицы Q найдем 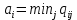- самый маленький, но гарантированный доход.

Правило Вальда рекомендует выбрать решение i₀ с наибольшим

a_i : i₀ =max_i(min_jq_ij)

В каждой строке матрицы Q найдем минимальное значение. В ячейку В10 введем функцию =МИН(B3:F3) и скопируем ее в ячейки В11, В12 и В13.



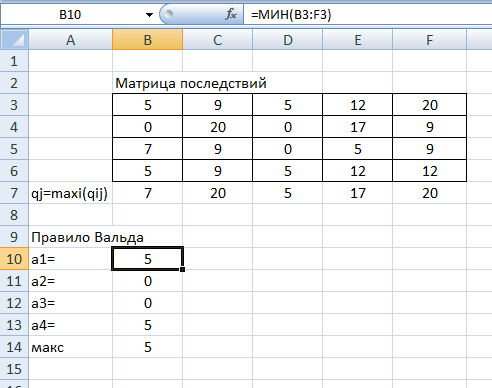
Рис.7. Результаты расчетов по правилу Вальда

Получили: а₁ = 5, а₂ = 0, а₃ = 0, а₄ = 5.

Среди всех чисел а_i выберем наибольшее. Наибольшее значение а₁ = а₄ =5.

Значит, правило Вальда рекомендует принять первое или четвертое решение.

---

Определим решение по правилу Сэвиджа(правило минимального риска).

Правило Сэвиджа рекомендует принять решение 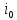с наименьшим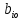



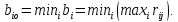
Рассматривая каждое решение, в каждой строке матрицы R найдем максимальный риск .

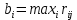Расчеты выполним в Excel. В ячейку G10 введем функцию =МАКС(H3:L3) и скопируем ее в ячейки G11, G12 и G13.

Получили:

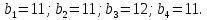
Выберем наименьшее 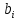. Наименьшее значение .



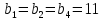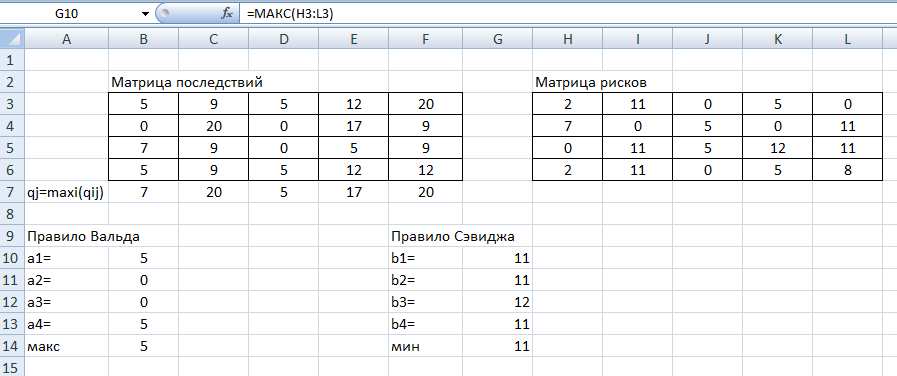
Рис.8. Результаты расчетов по правилу Сэвиджа.

Правило Сэвиджа рекомендует принять первое, второе и четвертое решение.

Применим правило Гурвица. (взять λ равному 0,5; 0,4 и 0,3).

По правилу Гурвица взвешиваются пессимистический и оптимистический подходы и принимается решение i, при котором достигается максимум



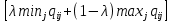
Рассмотрим различные значения :

1. 
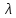   При .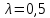
   

Проанализируем каждое решение. Для каждой строки матрицы Q вычислим величину параметра 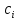. Для этого в ячейку В18 введем функцию =$B$17*МИН(B3:F3)+(1-$B$17)*МАКС(B3:F3).

И скопируем ее в ячейки В19, В20 и В21. Получили:



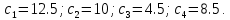
Максимальное значение .

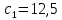Следовательно, при 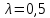, правило Гурвица рекомендует первое решение.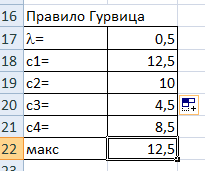

---

Рис.9

Аналогично проведем вычисления для остальных значений .

2. 
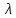   При .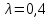
   

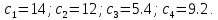
Максимальное значение .

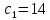При 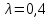, правило Гурвица рекомендует первое решение.

3. 
   При .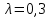
   

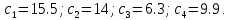
Максимальное значение .

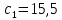При 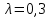, правило Гурвица рекомендует первое решение.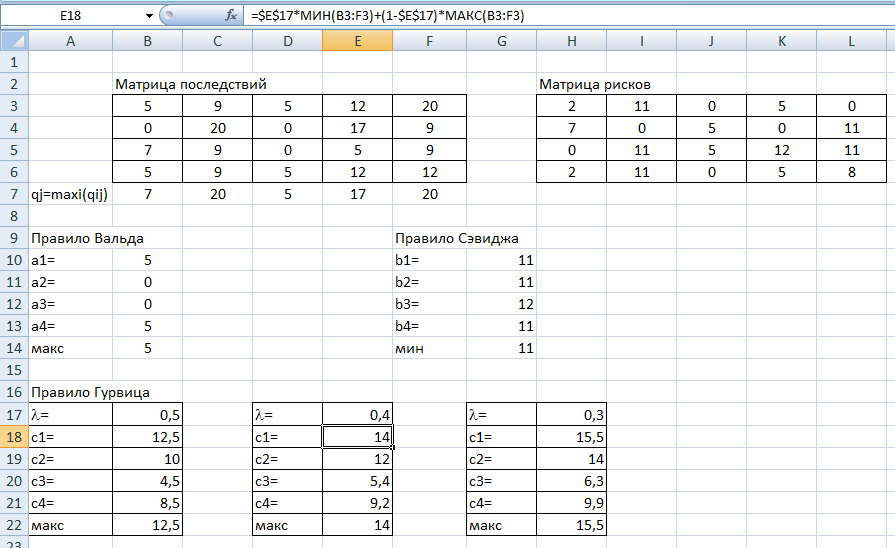



Рис.10. Результаты вычисление по правилу Гурвица
Примененные правила не дают однозначной рекомендации. В таких случаях выбирается то решение, которое рекомендуется чаще других. Рекомендации оформим в виде таблицы.

Решение	Критерии					Число решений, принятых по разным критериям
	Вальда	Сэвиджа	Гурвица
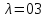А1	+	+	+	+	+		5
А2		+					1
А3
А4	+	+					2

---

Смотрите также файлы

• Лабораторная работа 8 Исследование простейшей демографической модели Мальтуса.doc

• Практическая работа по теме "Растровая графика".docx

• Тема Анализ эффективности рекламной деятельности в первом блоке.pdf

• Программа доо Химическая лаборатория.docx

• Занятие по математике в подготовительной группе Веселая математика вместе с Буратино.docx