Файл: Высшего образования финансовый университет при правительстве российской федерации.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Однозначно нужно выбрать первое решение.
3)Проведите анализ ситуации частичной неопределенности при известных вероятностях того, что реальная ситуация развивается по варианту j: 0,25; 0,2; 0,3; 0,15; 0,1 (примените правила максимизации среднего ожидаемого дохода и минимизации среднего ожидаемого риска).
Решение сделаем в Excel. Подготовим матрицы последствий и рисков и введем вероятности того, что реальная ситуация развивается по варианту
j: 0,25; 0,2; 0,3; 0,15; 0,1
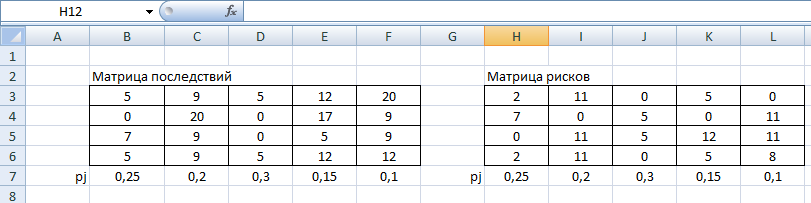
Рис. 11
Применим правило максимизации среднего ожидаемого дохода.
Доход, получаемый фирмой при реализации i-го решения, является случайной величиной
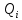 , с рядом распределения
, с рядом распределения 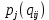 . Математическое ожидание
. Математическое ожидание 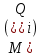 и есть средний ожидаемый доход, обозначаемый также
и есть средний ожидаемый доход, обозначаемый также 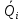 . Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.
. Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.Найдем средний ожидаемый доход для каждого решения при указанных вероятностях. Для этого в ячейку C10 введем функцию: =СУММПРОИЗВ($B$7:$F$7;B3:F3) и скопируем ее в ячейки C11, C12, C13. Получим: М(Q1) = 8,35; М(Q2) = 7,45; М(Q3) = 5,2; М(Q4) = 7,55.
Определили, что максимальный средний ожидаемый доход равен 8,35 и соответствует первому решению.
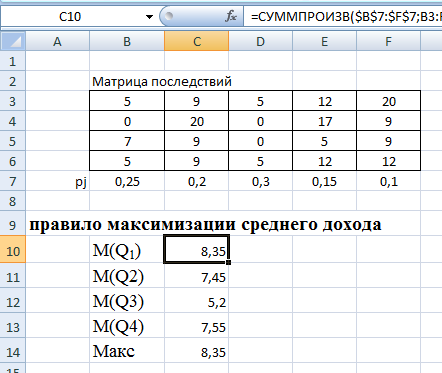
Рис.12. Результаты расчетов по правилу максимизации среднего ожидаемого дохода.
Правило минимизации среднего ожидаемого риска.
Риск фирмы при реализации i-го решения является случайной величиной
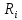 рядом распределения
рядом распределения 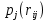 . Математическое ожидание,
. Математическое ожидание, 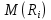 и есть средний ожидаемый риск, обозначаемый также
и есть средний ожидаемый риск, обозначаемый также 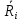 . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
Вычислим средние ожидаемые риски при указанных вероятностях для каждого решения. В ячейку I10 введем функцию: =СУММПРОИЗВ($H$7:$L$7;H3:L3) и скопируем ее в ячейки I11, I12, I13. Получим средние риски: М(R1) = 3,45; М(R2) = 4,35; М(R3) = 6,6; М(R4) = 4,25.
Правило рекомендует принять решение, влекущее минимальный средний риск. Минимальный средний риск равен 3,45 и соответствует первому решению.
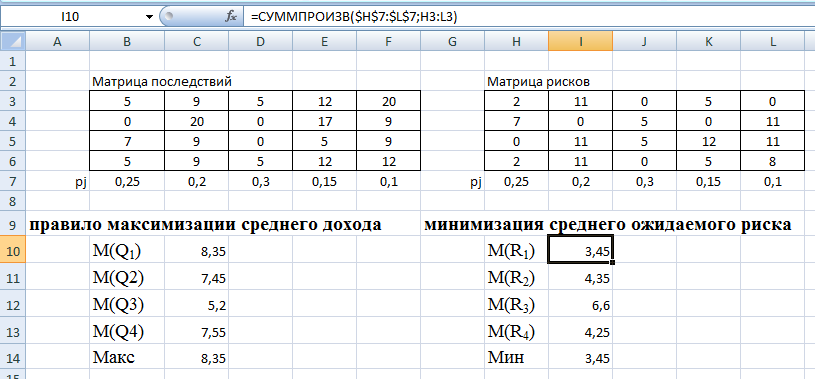
Рис.13. Результаты расчетов по правилу минимизации среднего ожидаемого риска.
В условиях частичной неопределенности нужно выбирать только первое решение.

Решение.
Портфель минимального риска с заданной доходностью находится по формуле Х = V-1(λI + ν
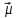 ).
).Для нахождения портфеля предварительно надо вычислить:
- обратную матрицу V-1;
- константы (при этом константы α, γ, ???? – положительные числа):
- α = ITV-1I, β = ITV-1
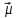 =
= 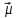 TV-1I,
TV-1I,- γ =
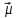 TV-1
TV-1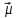 , ???? = αγ – β2;
, ???? = αγ – β2;- λ =
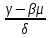 ; ν =
; ν = 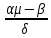 .
.Вычисления проведем в Excel.
Внесем исходные данные.
Р
 ис.14. Исходные данные
ис.14. Исходные данныеВведем зависимости.
Уравнение минимальной границы имеет вид:
σ =
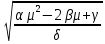
| Формула | Ячейка | Функция для вычисления |
| V-1 | B6:D8 | {=МОБР(C2:E4)} |
| ITV-1 | B10:D10 | {=МУМНОЖ(O2:Q2;B6:D8)} |
| α = ITV-1I | G6 | {=МУМНОЖ(B10:D10;M2:M4)} |
| β = ITV-1 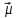 | G8 | {=МУМНОЖ(B10:D10;H2:H4)} |
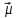 TV-1 TV-1 | B12:D12 | {=МУМНОЖ(O4:Q4;B6:D8)} |
| γ = 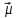 TV-1 TV-1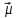 | G10 | {=МУМНОЖ(B12:D12;H2:H4)} |
| ???? = αγ-β2 | K6 | =G6*G10-C8^2 |
| λ = γ-βμ/???? | K8 | =(G10-G8*K3)/K6 |
| ν = αμ-β/???? | K10 | =(G6*K3-G8)/K6 |
| λI+ν 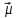 | F15 | =$K$8*B15+$K$10*D15 |
| F16:F17 | Скопировать формулу из ячейки F15 | |
| X = V-1(λI+ν 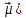 | С19:С21 | {=МУМНОЖ(B6:D8;F15:F17)} |
| XT | J16:L16 | {=ТРАНСП(C19:C21)} |
| XTV | J18:L18 | {=МУМНОЖ(J16:L16;C2:E4)} |
| XTVX | J20 | {=МУМНОЖ(J18:L18;C19:C21)} |
| σ | J20 | =КОРЕНЬ(J20) |
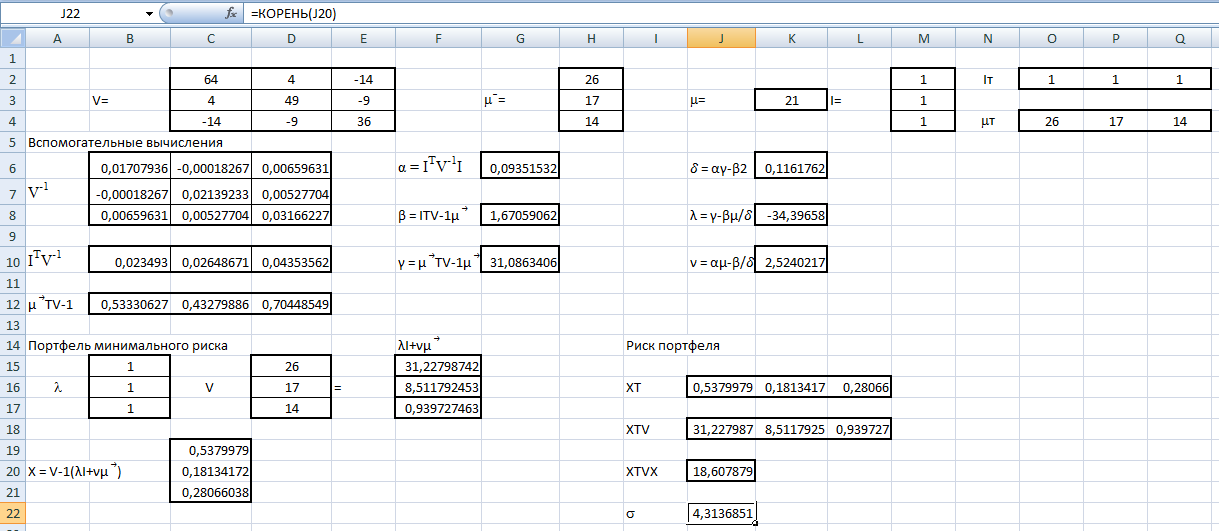
Рис.15. Результаты расчета портфеля минимального риска
Получили: Х = (0,538; 0,181; 0,281). Чтобы обеспечить доходность портфеля
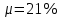 необходимо взять 53,8% бумаг первого вида; 18,1% - второго и 28,1% - третьего вида.
необходимо взять 53,8% бумаг первого вида; 18,1% - второго и 28,1% - третьего вида.Риск каждой бумаги определим по ковариационной матрице: по диагонали стоят дисперсии, поэтому для рисков бумаг имеем:
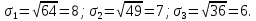
Риск портфеля равен 4,31 и оказался меньше риска первой бумаги (σ1=8), второй (σ1=7) и третьей (σ1=6) бумаг. При этом доходность портфеля μ=21% на 5% меньше доходности первой бумаги, на 4% больше доходности второй и на 7% больше доходности третьей бумаги.
Уравнение минимальной границы имеет вид:
σ =
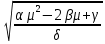
Подставляя в нее найденные значения констант α=0,09; β=1,67; γ=31,09; ????=0,12 получим
σ =
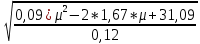 =
= 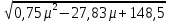 .
.Итак, минимальная граница имеет вид σ =
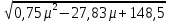 .
.
Решение.
При ρ1 = 0,3, q1 = 150, К1 = 108; ρ2 = 0,2, q2 = 70, К2 = 104, m=2
воспользуемся формулой
ρ =
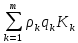 /
/ 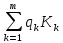 , где
, где ρk – доходность облигации,
qk – количество облигаций данного вида,
Kk – курс облигации.
Вычисления выполним в Excel.
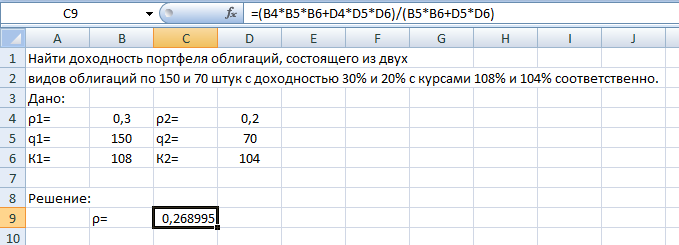
Рис.16. Результаты вычислений поиска доходности портфеля облигаций
Ответ: Доходность портфеля облигаций равна ρ ≈ 0,269.