ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 6
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
КСП
Предмет: Математика
| Раздел долгосрочного планирования: Отношения и пропорция | Школа: Средняя школа лицей №27 | | ||
| Дата: 04.10.2022 | ФИО учителя: Темиргалиева Ж.М. | | ||
| Класс: 6Д | Присутствовало: | Отсутствовали: | ||
| Тема урока: | Длина окружности. Площадь круга. Шар. Сфера. | | ||
| Цели обучения, достигаемые на этом уроке (Ссылка на учебный план) | 6.3.3.2 знать, что отношение длины окружности к ее диаметру есть число постоянное; 6.3.3.3 знать и применять формулу длины окружности; 6.3.3.4 знать и применять формулу площади круга. | | ||
| Цель урока | Все ученики: Определяютотношение длины окружности к ее диаметру. Знают, что отношение длины окружности к ее диаметру есть число постоянное. Знают значение числа . Воспроизводят формулу длины окружности и формулу площади круга. Решают задачи на нахождение длины окружности и площади круга по формулам. Большинство учеников: Находят длину окружности, результат округляют. Находят площадь кольца, используя формулу площади круга. Некоторые ученики: Решают задачи прикладного характера, составляя алгоритм. | | ||
| Критерии оценивания | Обучающийся: Показывает, что отношение длины окружности к ее диаметру есть число постоянное. Формулирует формулу длины окружности. Формулирует формулу площади круга. Решает задачи на нахождение длины окружности. Решают задачи на нахождение площади круга. | | ||
Ход урока
| Время / этапы урока | Деятельность учителя Каким образом я достигну целей обучения? | Деятельность учащихся | Оценивание (метод/ прием/ техника/ стратегия) | Ресурсы | |||||||||||||||||||||
| Начало урока Орг. момент 1 мин | Учитель делит учащихся на группы. На столе лежат геометрические фигуры: квадрат, круг, прямоугольник, треугольник. Учащиеся, выбирая одну геометрическую фигуру, делятся на группы. Мы живём с братишкой дружно, Нам так весело вдвоём, Мы на лист поставим кружку, Обведём карандашом. Получилось то, что нужно – Называется … (ОКРУЖНОСТЬ) Совместная постановка цели урока. | Учащиеся выбирают геометрическую фигуру и рассаживаются по группам. Учащиеся, видя тему урока, пробуют определить цель урока. | | | |||||||||||||||||||||
| Актуализация опорных знаний 5 мин | Работа в группах. Стратегия «Горячий стул». Учащиеся в группах составляют вопросы по теме «Окружность». Представитель от каждой группы идёт в другую группу и садится на стул. Ученики из других групп задают составленные вопросы. Учитель ходит по группам, подводит итог работы, отмечает лучшие вопросы и ответы. | Составляют вопросы в группах по теме «Окружность». Задают вопросы представителю другой группы. | Устный комментарий учителя. Взаимооценивание. Смайлики. | Диалог и поддержка учителя. | |||||||||||||||||||||
| Основная часть 10 мин | Работа в парах. Исследовательская работа. Сегодня на уроке мы познакомимся с формулой для вычисления длины окружности и площади круга, научимся применять их для решения задач. Вы знаете, что длину отрезка можно измерить с помощью линейки. А как измерить длину окружности, если сама окружность – кривая линия? Я просила Вас принести на урок стакан и нитку. Вам после проведённого исследования необходимо будет заполнить таблицу:
Алгоритм исследования: Поставьте стакан на лист бумаги и обведите его карандашом. На бумаге получим замкнутую кривую линию – окружность. Обведите стакан ниткой (один раз) так, чтобы конец нитки совпал с началом в одной и той же точке окружности. Выпрямите эту нитку и по линейке измерьте ее длину, это и будет длина окружности. Найдите по рисунку диаметр окружности, измерьте его с помощью линейки. Вычислите отношение длины окружности к её диаметру. Длину окружности обозначают буквой С. Заполните таблицу. Вывод: Вы принесли стаканы разного диаметра, соответственно длина нитки, которой вы обведёте стакан, будет разной. Какой вывод Вы можете сделать? Чему равно отношение длины окружности к её диаметру? Если мы каждый раз будем так измерять длину окружности, то это будет слишком долго, не всегда возможно. Поэтому существует формула, но перед тем как к ней перейти познакомимся с числом пи. Длина окружности прямо пропорциональна длине её диаметра. Поэтому для всех окружностей отношение длины окружности к длине её диаметра является одним и тем же числом. Это число обозначают греческой буквой (читается пи). Если обозначить длину окружности буквой С, а длину диаметра буквой D, то С:D=. Поэтому С=D. Так как D=2R, то С=2R. Подсчёты показали, что с точностью до десятитысячных =3,1416 (22/7). Если значение округлить до сотых, то получим значение 3,14. Рассмотрим круг. Фигура, ограниченная окружностью, называется кругом. Круг имеет свою площадь, но не имеет длины. Площадь круга вычисляется по формуле:. | Выполняют построения и измеряют линейкой длину, полученной линии. Определяют отношение длины окружности к её диаметру. | Наблюдение. Устный комментарий учителя. Самооценивание степени понимания. Палец — большой вверх для положительной оценки, вниз — для отрицательной. | Диалог и поддержка учителя. Поддержка между учащимися. Диалог и поддержка учителя. | |||||||||||||||||||||
| Закрепление 8 мин | Работа в группах. Решают задания из учебника. Каждый ученик решает 4 задачи, выбрав любые исходные данные. Затем учащиеся выполняют взаимопроверку внутри группы при помощи активной стратегии «Карусель». По итогам работы учитель группам предлагает правильное решение на доске для взаимооценивания. № 245, 246, 247, 248 (А.Е.Абылкасымова) №245 Найдите длину окружности, если длина её радиуса равна 5см; 3,5м; 12мм. №246 Найдите длину радиуса окружности, если её длина равна 56см; 7м; 18,6м. №247 Найдите площадь круга, длина радиуса которого равна 6см; 12м; 3,5см. №248 Найдите длину радиуса круга, площадь которого равна 314м2; 12,56м2; 78,5см2. | С целью закрепления знаний, учащиеся решают задачи в группе, обсуждают и выполняют взаимопроверку и взаимооценивание, используя дескрипторы и верные ответы, предложенные учителем: Дескрипторы: Обучающийся - использует формулу длины окружности; - находит длину окружности; - находит длину радиуса окружности; - использует формулу площади круга; - находит площадь круга; - находит длину радиуса круга. | Учащиеся комментируют количество правильно решенных задач в группе. | По заданию и результату. | |||||||||||||||||||||
| Самостоятельная работа 10 мин | Индивидуальная работа. Учитель раздает карточки с заданиями по вариантам. (Приложение 2). | С целью определения уровня усвоения материала учащиеся пишут самостоятельную работу. Дескрипторы: Обучающийся - использует формулу длины окружности; - находит длину окружности; - округляет результат; - составляет алгоритм решения; - использует формулу для нахождения площади круга; - вычисляет площади кругов; - вычисляет площадь кольца; - находит площадь квадрата; - находит радиус круга; - вычисляет площадь заштрихованной части фигуры; - решает задачу прикладного характера, составляя алгоритм. | Оценивание учителем после урока. | По заданию и результату. | |||||||||||||||||||||
| 1 вариант 1.Радиус окружности равен 3см. Найдите длину окружности. Результат округлите до десятых. 2.Длина радиуса большей окружности равна 21см, длина радиуса меньшей окружности – 16см. Вычислите площадь кольца, образованного этими окружностями. 3. Вычислите площадь заштрихованной фигуры. | 2 вариант 1.Радиус окружности равен 4см. Найдите длину окружности. Результат округлите до десятых. 2.Длина радиуса большей окружности равна 17см, длина радиуса меньшей окружности – 7см. Вычислите площадь кольца, образованного этими окружностями. 3. Вычислите площадь заштрихованной фигуры. | ||||||||||||||||||||||||
| 4*. 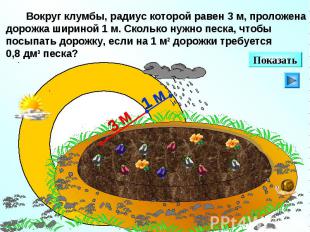 | |||||||||||||||||||||||||
| Конец урока Домашнее задание 2 мин | Учитель информирует о домашнем задании. Самостоятельно разобрать такие понятия как шар и сфера. Желающим подготовить презентацию по данной теме в виде … (по желанию учащихся). Решить задачу стр.57. №251, задачу по рисунку. №251 На фото вы видите архитектурный символ выставки Астана ЭКСПО-2017. Центральным элементом Выставочного комплекса «Нұр Әлем» является самое большое сферическое здание в мире. 1.Найдите длину диаметра этой сферы, вычислив значение выражения (5,6+89,7-56,007+40,707)м. 2.Найдите высоту здания, вычислив значение выражения (7,456,56:8,08+48,2)м.  | Учащиеся уточняют, задают вопросы по домашнему заданию. | | | |||||||||||||||||||||
| Рефлексия 4 мин | Стратегия «Лесенка успеха». | Учащиеся оценивают свою деятельность на уроке. Приклеивают стикеры на ступени, которых достигли. | Самооценивание знания и понимания, применения. | Диалог и поддержка учителя. | |||||||||||||||||||||
