Файл: Контрольная работа Дискретная математика и Теория вероятностей.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 14
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
до 
: 
Ответ: выделенные элементы и графики в решении.
105. Величина
распределена по нормальному закону с параметрами 
и 
. Найти среднее значение (математическое ожидание), дисперсию и среднеквадратичное отклонение . Аналитически записать и изобразить графики функции плотности вероятности и функции распределения вероятности . Определить вероятности того, что при единичном испытании примет значение: от 
до 
; от 
до 
; от 
до 
.Решение.
1. Математическое ожидание (по свойствам нормально распределенной величины):
2. Дисперсия (по свойствам нормально распределенной величины):
3. Среднеквадратичное отклонение:
.4. График функции распределения (по свойствам нормально распределенной величины).
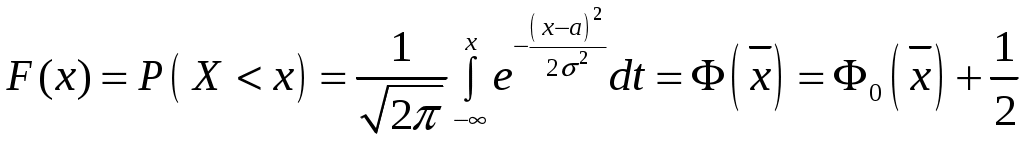,где
.
 |  |  |  |
 |  |  |  |
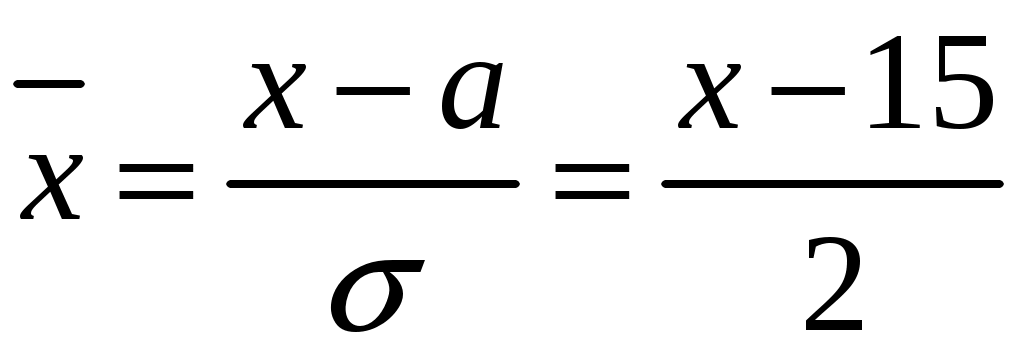
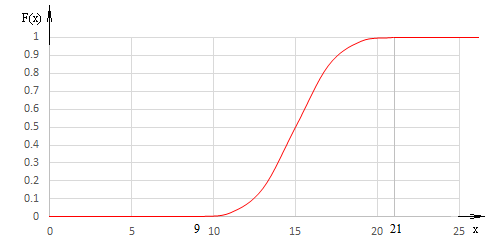
5. График функции плотности распределения.
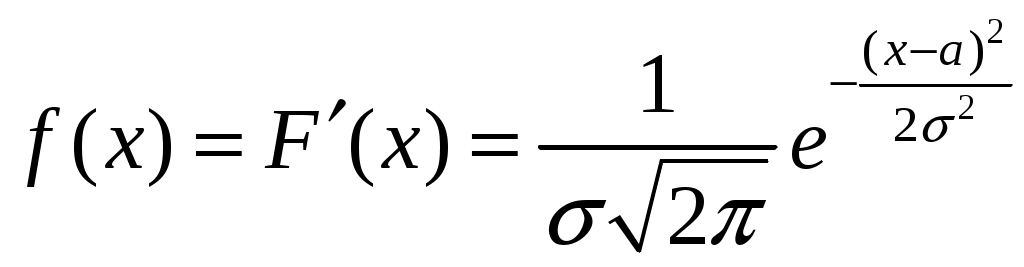, где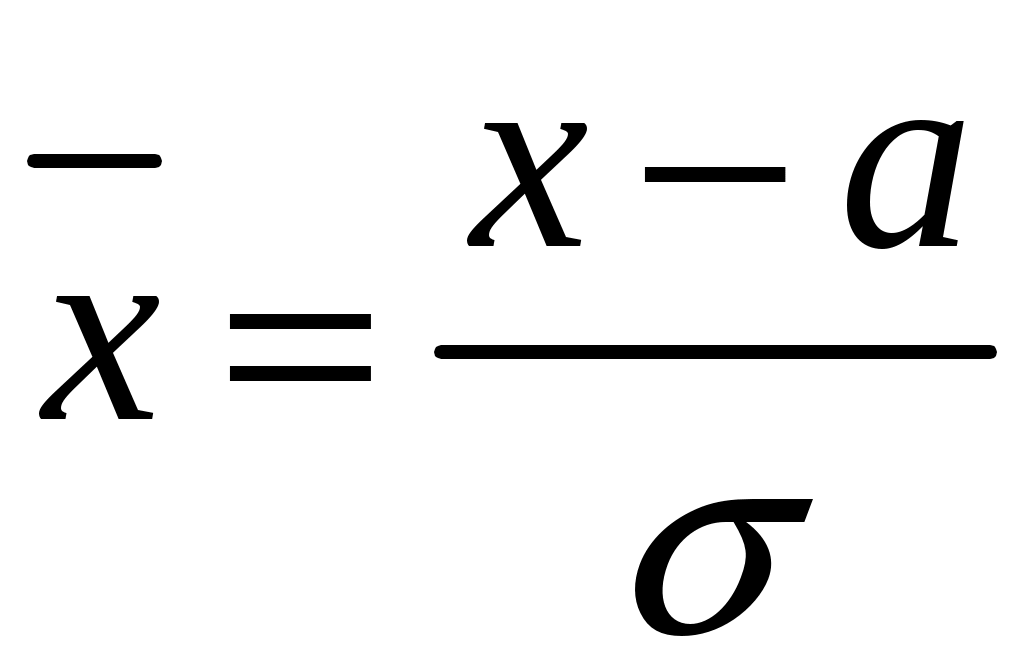 
.| | |   | |
 | |  |  |
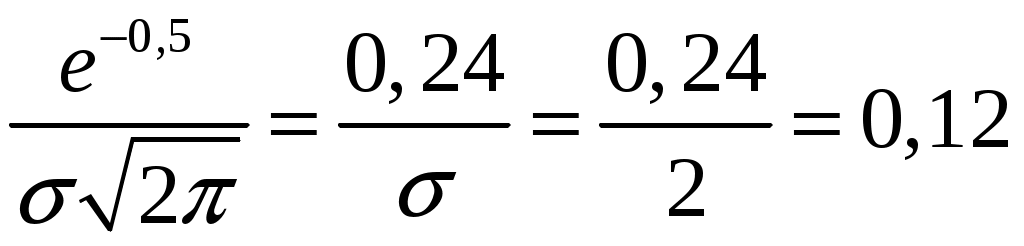| Прим. | Линия практически горизонтальна | Точки перегиба | максимум |
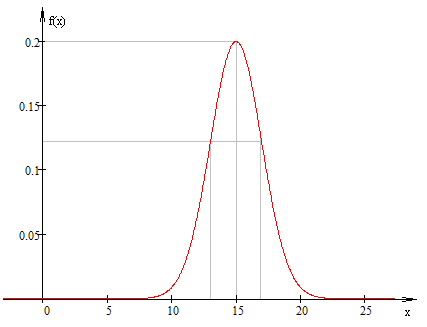
6. Найдем вероятности:
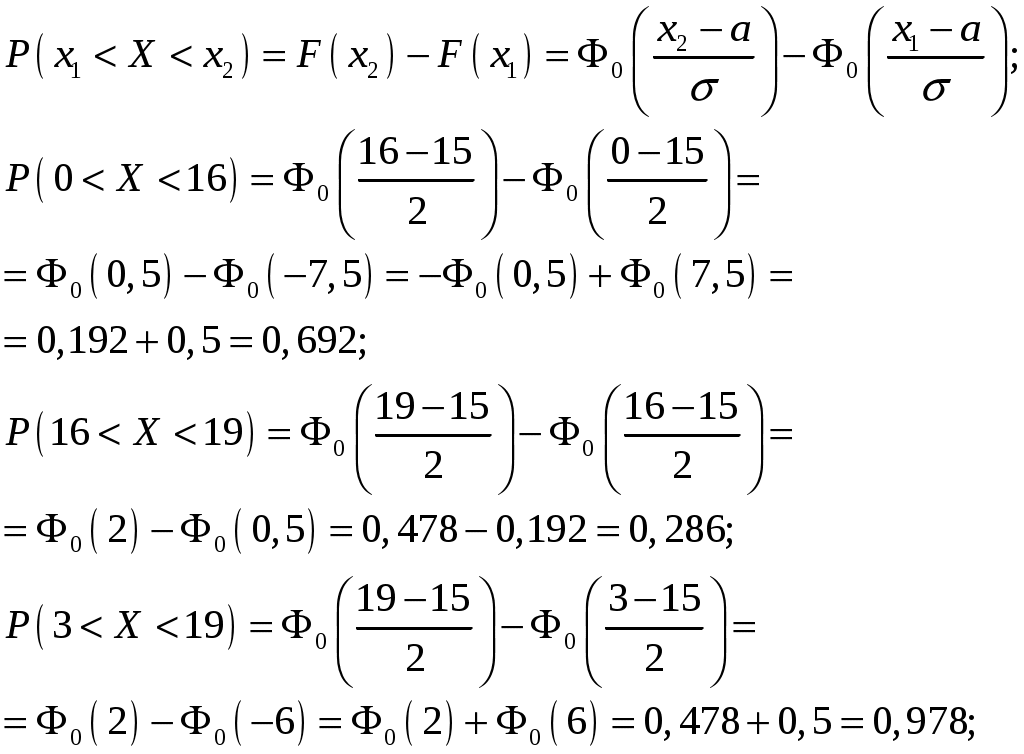
Ответ: выделенные элементы и графики в решении.