Файл: Курсовой проект по дисциплине Инженерные конструкции сооружений (наименование дисциплины) Проектирование железобетонного резервуара.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 44
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Расчетная схема для определения усилий в полке, окаймленной двумя продольными и двумя поперечными ребрами плиты покрытия, представляет собой защемленную по краям четырёхугольную пластинку (рисунок 1.3), загруженную равномерной нагрузкой.
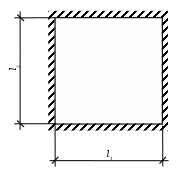
Рисунок 1.3 – Защемленная по краям полка, окаймленная двумя продольными и двумя поперечными ребрами плиты покрытия
Расстояние в свету между двумя поперечными ребрами плиты (одно из этих ребер является средним) на уровне низа полки
.Расстояние в свету между двумя продольными ребрами плиты на уровне низа полки
.Расстояния
и 
примерно равны и рассматриваемую часть полки можно считать практически квадратной.Равномерно распределенная нагрузка для расчета полки плиты по предельным состояниям первой группы
.При расчете полки плиты по методу предельного равновесия расчетное значение (для предельных состояний первой группы) изгибающего момента на опорах и в середине пролетов (отнесенное к полосе шириной 1 м)
.Поперечные ребра плиты покрытия можно рассматривать как свободно опертые балки (пренебрегая некоторым защемлением поперечных ребер в продольных ребрах).
Расчетная схема для определения усилий в среднем поперечном ребре плиты покрытия приведена на рисунке 1.4.
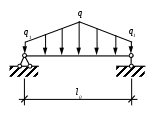
Рисунок 1.4 – Расчетная схема для определения усилий в среднем поперечном ребре плиты покрытия
Расчетный пролет поперечного ребра плиты равен расстоянию в свету между продольными ребрами на уровне низа поперечного ребра:
.Равномерно распределенная нагрузка от веса поперечного ребра плиты (для расчета по предельным состояниям первой группы)
.Максимальное расчетное значение (для предельных состояний первой группы) действующей на поперечное ребро плиты распределенной нагрузки
.Минимальное расчетное значение (для предельных состояний первой группы) действующей на поперечное ребро плиты распределенной нагрузки
.Максимальный изгибающий момент для расчета по предельным состояниям первой группы
.Максимальная поперечная сила для расчета по предельным состояниям первой группы
.1.4 Определение характеристик бетона и арматуры
Примем бетон класса по прочности на сжатие В 25.
Нормативное значение (расчетное значение для предельных состояний второй группы) сопротивления бетона осевому сжатию (призменная прочность)
.Нормативное значение (расчетное значение для предельных состояний второй группы) сопротивления бетона осевому растяжению
.Расчетное значение сопротивления бетона осевому сжатию для предельных состояний первой группы
.Расчетное значение сопротивления бетона осевому растяжению для предельных состояний первой группы
.Примем передаточную прочность бетона (прочность бетона к моменту его обжатия)
.Эту прочность следует назначать не менее 15 МПа и не менее 50 % принятого класса бетона по прочности на сжатие.
Начальный модуль упругости бетона при сжатии и растяжении
.Коэффициент ползучести
.
Примем в качестве предварительно напряженной арматуры арматуру класса A800 (A-V) по прочности на растяжение.
Нормативное значение (расчетное значение для предельных состояний второй группы) сопротивления арматуры растяжению
.Расчетное значение сопротивления арматуры растяжению для предельных состояний первой группы
.Примем в качестве предварительно ненапряженной продольной (а в ряде случаев – поперечной) арматуры арматуру класса А400 (A-III) по прочности на растяжение.
Нормативное значение (расчетное значение для предельных состояний второй группы) сопротивления арматуры растяжению
.Расчетное значение сопротивления арматуры растяжению для предельных состояний первой группы
.Расчетное значение сопротивления арматуры сжатию для предельных состояний первой группы
.Расчетное значение сопротивления поперечной арматуры (хомутов и отогнутых стержней) растяжению для предельных состояний первой группы
.Примем в качестве поперечной арматуры, арматуры сеток и сжатой продольной арматуры поперечного ребра плиты покрытия арматуру класса В500 (Вр-I) по прочности на растяжение.
Нормативное значение (расчетное значение для предельных состояний второй группы) сопротивления арматуры растяжению
.Расчетное значение сопротивления арматуры растяжению для предельных состояний первой группы
.Расчетное значение сопротивления арматуры сжатию для предельных состояний первой группы
.Расчетное значение сопротивления поперечной арматуры (хомутов и отогнутых стержней) растяжению для предельных состояний первой группы
.Модуль упругости принятой арматуры
.1.5 Расчет полки плиты покрытия на действие изгибающего момента
Подбор арматуры полки плиты выполняют как для изгибаемого элемента прямоугольного поперечного сечения высотой
и шириной 
.Рабочая высота поперечного сечения полки плиты
.Определим вспомогательную величину
.Определим по таблице вспомогательную величину
.Так как
, то требуемая площадь поперечного сечения продольной арматуры в растянутой зоне бетона 
.Расстояние между осями стержней продольной арматуры должно быть не более удвоенной высоты поперечного сечения элемента, т.е. не более 100 мм. Примем десять стержней диаметром 4 мм класса В500 с
= 126 мм2.1.6 Расчет поперечного ребра плиты покрытия на действие изгибающего момента
Рабочая высота поперечного сечения поперечного ребра плиты
.Определим по таблице вспомогательную величину
.Определим по таблице вспомогательную величину
.Значение
, вводимое в расчет, принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более
.Поперечное сечение поперечного ребра плиты покрытия приводим к эквивалентному тавровому (рисунок 1.5). Ширина ребра в запас прочности принята 50 мм.