Файл: Лабораторная работа 2 изучение характеристик электростатического поля проверил.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.04.2024

Просмотров: 46

Скачиваний: 0

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Минцифры

СибГУТИ

Кафедра физики

Лабораторная работа 3.2

ИЗУЧЕНИЕ ХАРАКТЕРИСТИК ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Выполнил:

Проверил:

Измерения сняты _____________________________________________

Дата, подпись преподавателя
Отчет принят _____________________________________________

Дата, подпись преподавателя
Защита _____________________________________________

Оценка, дата, подпись преподавателя

Новосибирск, 2022 г

  1. ЦЕЛЬ РАБОТЫ

Исследовать электростатическое поле, графически изобразить сечение эквипотенциальных поверхностей и силовые линии для некоторых конфигураций поля.

  1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ


В пространстве любое заряженное тело создает вокруг себя

электромагнитное поле, которое взаимодействует с внешним электромагнитным полем. Электромагнитное поле действует на помещенные в него электрические заряды с силой, пропорциональной величине заряда и не зависящей от скорости движения заряда – это является основным свойством электромагнитного поля. Электростатическое поле – поле, создаваемое неподвижными зарядами. Определить величину взаимодействия между зарядами можно благодаря Закону Кулона, который записывается по формуле:

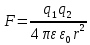; (1)

где 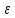– диэлектрическая проницаемость, характеризующая среду между зарядами, 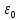– электрическая постоянная, 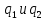– абсолютные величины взаимодействующих зарядов, 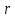– расстояние между ними.

В каждой точке пространства электростатическое поле характеризуется двумя величинами: потенциалом и напряженностью:

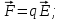(2)

Электрическое поле можно охарактеризовать также потенциалом – энергетической величиной, численной равной работе по переносу единичного, положительного, точечного заряда q из данной точки поля в бесконечность:


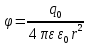; (3)
С работой сил электрического поля по перемещению точечного заряда из точки с потенциалом 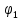в точку с потенциалом 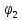связана разность потенциалов следующим образом:

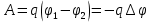; (4)

Электростатическое поле графически принято изображать в виде силовых линий и эквипотенциальных полей. Силовые линии электрического поля – это линии, проведенные в пространстве таким образом, чтобы касательная к ним совпадала с направлением вектора E  в данной точке.



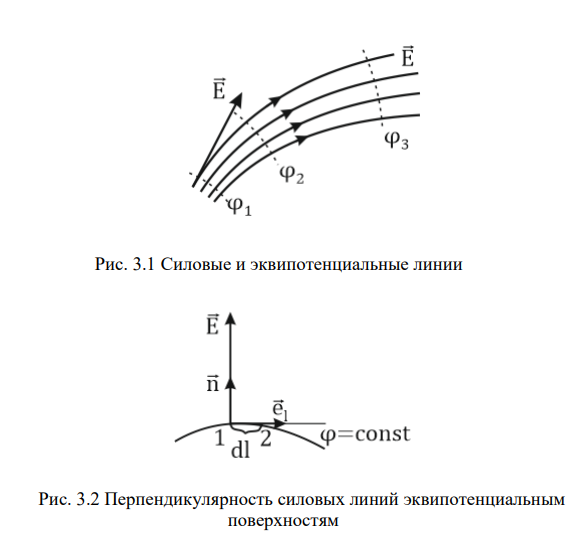
Поверхности, во всех точках которой потенциал имеет одно и то же значение называются эквипотенциальными. Эти поверхности целесообразно проводить так, чтобы разность потенциалов между соседними поверхностями была одинаковой. Тогда по густоте эквипотенциальных поверхностей можно наглядно судить о значении напряженности поля в разных точках. Величина напряженности больше там, где гуще эквипотенциальные поверхности.

Свойства силовых линий, следующие:

1) Начинаются на положительных зарядах, заканчиваются на отрицательных зарядах. В данной работе заряды располагаются на внешней поверхности металлических электродов.

2) Перпендикулярны эквипотенциальным поверхностям, в том числе поверхностям электродов.

3) В тех областях поля, где силовые линии расположены ближе друг к другу, величина напряженности поля больше.

4) Направлены в сторону наиболее быстрого убывания потенциала.

Расчитаем работу при малом перемещении 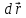для нахождения связи между напряженностью и потенциалом:

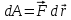; (5)

Выражение для напряженности в трехмерном пространстве:

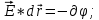(6)

Для случая одномерного пространства при перемещении заряда вдоль оси х на расстояние dx при фиксированных значениях координат у и z ( dy  dz  0 ):


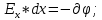(7)

Выразив эту формулу через 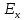получим:

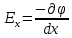; (8)

На другие оси координат получить выражения можно по аналогии:

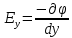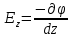; ; (9)

Вектор напряженности можно построить, используя полученные векторы осей декартовых координат:

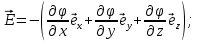(10)

Сокращенно данное выражение можно записать так:

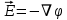; (11)

Вектор функции, характеризующий скорость пространственного изменения функции и направленный в сторону максимального возрастания называется градиентом функции.

Погрузив заряженные тела в проводящую среду, в ней потечет электрический ток. Для того, чтобы ток не прекращался, необходимо непрерывное возобновление исходных зарядов путем подключения тел к внешнему источнику. В каждой точке среды ток характеризуется плотностью тока 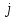- величиной тока, приходящейся на единицу площади, перпендикулярной направлению тока. Между плотностью тока и напряженностью электрического поля существует связь, называемая законом Ома в дифференциальной форме:

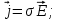(12)

где 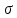- удельная электропроводность среды, величина, обратная удельному сопротивлению. При постоянном токе распределение заряда в пространстве не изменяется, и электрическое поле точно такое же, как и в электростатическом случае.

  1. Описание лабораторной установки

Установка представляет собой прямоугольную ванну с водой, в которую погружены два неподвижных электрода различной формы Электроды присоединены к источнику постоянного низковольтного напряжения ИН. Также имеется подвижный электрод (зонд) З, с помощью которого студент исследует распределение потенциала в ванночке между 6 электродами. Вольтметр показывает напряжение между отрицательно заряженным электродом и точкой в ванне, в которую помещен зонд.






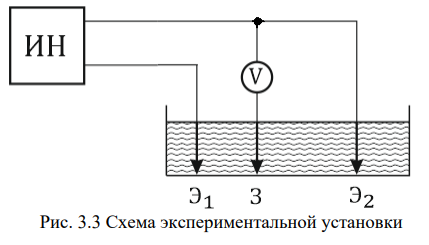
Плоский электрод заряжен отрицательно, круглый – заряжен положительно. Потенциал отрицательно заряженного электрода принимается равным НУЛЮ. Точки, для которых вольтметр показывает одинаковое значение разности потенциалов, относятся к одной и той же эквипотенциальной поверхности. Виртуа ьная лабораторная установка является программным симулятором реального лабораторного оборудования и позволяет смоделировать на персональном компьютере поведение настоящего электрического поля, создаваемого используемой конфигурацией электродов ванны, и получить значения измеряемых физических величин, находящиеся в соответствии с реальным экспериментом.



  1. Задание

Вариант №1

Потенциал, В
Координаты точек

№1
№2
№3
№4
№5
№6
№7

x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см

2
18,50
9,45
17,60
8,70
17,50
7,80
17,90
6,96
18,80
6,50
19,90
6,80
19,90
9,20

3
19,70
10,10
18,60
10,20
17,40
9,48
16,90
8,52
17,00
7,30
17,60
6,35
19,00
5,78

4
19,5
11,90
18,50
11,90
16,90
11,20
15,50
9,09
15,60
6,39
17,50
4,43
19,80
4,13

5
10,00
15,70
9,95
12,70
10,00
10,30
10,00
7,13
10,00
5,43
10,00
3,30
9,95
0,61

6
1,00
11,90
3,21
11,00
4,36
9,61
4,68
8,04
4,27
6,22
2,36
4,39
0,32
4,09

7
0,14
10,00
1,68
10,10
2,64
9,43
3,14
8,09
2,68
6,65
1,36
5,83
0,14
5,96

8
0,14
9,26
1,14
9,52
1,95
9,17
2,50
8,26
2,18
7,04
1,32
6,52
0,27
6,65




C

B

A














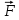
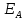
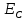
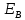
Рис. 1

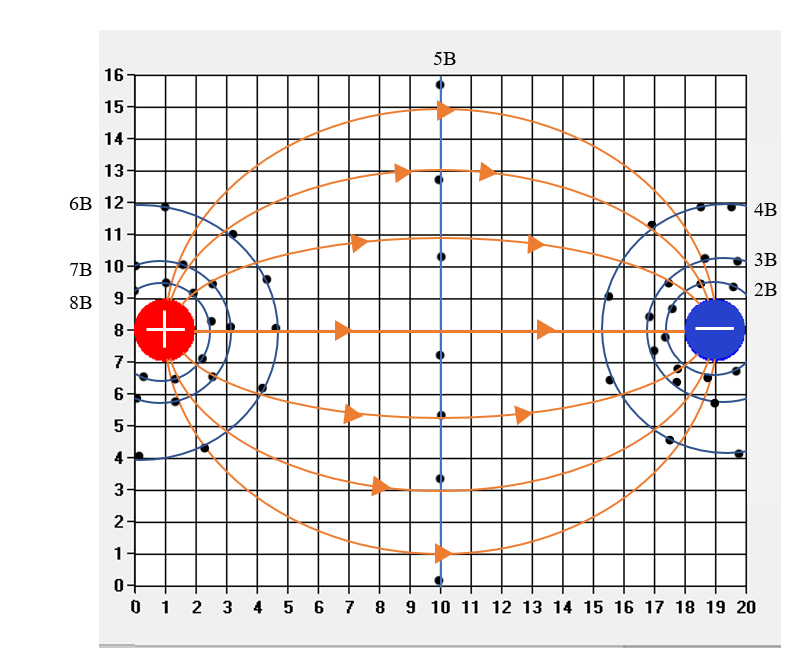
Найдем величину электрического поля в точке с помощью формулы: ;

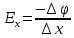Координаты точек для расчета возьмем из условий задания, а именно:

А (3,8), B (10, 8), С (16,8).

;

;

;

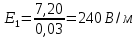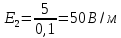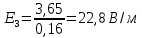Величину силы, действующей на электрон, помещенный в каждую из этих точек найдем по формуле: ;







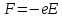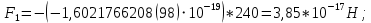
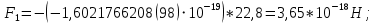
Вариант №2

Потенциал, В
Координаты точек

№1
№2
№3
№4
№5
№6
№7

x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см
x, см
y, см

2
1.23
15.60
1.23
13.00
1.18
10.70
1.18
7.83
1.18
5.52
1.23
3.48
1.23
0.61

3
3.27
15.70
3.27
13.50
3.18
11.10
3.23
8.91
3.18
6.43
3.18
3.78
3.00
0.87

4
8.50
15.60
8.14
13.00
8.05
10.80
7.91
8.04
8.00
5.26
8.18
3.04
8.50
0.48

5
19.40
14.60
16.80
13.40
15.00
11.70
14.00
8.91
14.10
6.35
15.20
4.09
19.80
1.30

6
19.70
10.80
18.00
10.60
16.90
9.70
16.30
8.17
16.80
6.39
18.00
5.39
19.70
5.22

7
19.90
9.61
18.60
9.76
17.90
9.38
17.20
8.14
17.40
7.19
18.20
6.38
19.50
6.24

8
20.00
8.93
19.30
9.29
18.60
9.26
17.80
8.60
17.70
7.81
18.30
6.88
19.40
6.71

Смотрите также файлы