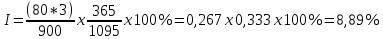Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная ДОТ

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

____________Корпоративные финансы___________



Группа ММ20М571
Студент
Бабкин М.В.


МОСКВА 2023


Задание 1

Вам поручено провести анализ досрочно погашаемой корпоративной облигации с номиналом 1000 рублей и 12% ставкой купона, который выплачивается раз в год, со сроком до погашения 20 лет и условием досрочного выкупа не ранее, чем через 4 года по курсу 112% номинала.

Текущий курс облигации 116% от номинала.

Требуется определить:

a. текущую доходность облигации

b. приблизительную доходность к погашению

c. полную доходность к погашению

d. приблизительную доходность к досрочному погашению (отзыву)

e. полную доходность к досрочному погашению (отзыву).
Решение:

1. 
   Текущая доходность определяется по формуле:
   

CY = 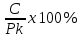, где: C – годовой процентный купонный доход; Pk - текущий рыночный курс.

Найдём годовой процентный купонный доход:

С = 1000 * 12% = 120 руб.

Вычислим текущий рыночный курс:

Pk = 1000 * 1,16 = 1 160 руб.

Определим текущую доходность:

2. 
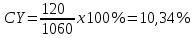
   Приблизительная доходность к погашению определяется по формуле:
   

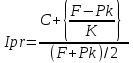, где С – годовой процентный купонный доход; Pk – текущий рыночный курс; F – номинал облигации; n – годы, остающиеся до погашения.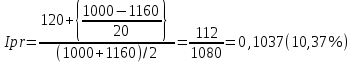

2. 
   Полная доходность к погашению определяется по формуле:
   

---

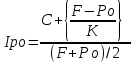, где С – годовой процентный купонный доход; Po – курс отзыва; F – номинал облигации; n – годы, остающиеся до погашения.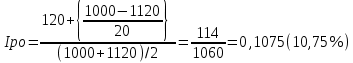

2. 
   Приблизительная доходность к досрочному погашению (отзыву) определяется по формуле:
   

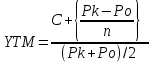, где С – годовой процентный купонный доход; Pk – текущий рыночный курс; Po – курс отзыва; n – лет к погашению.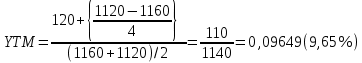

2. 
   Определим полную доходность к досрочному погашению (отзыву):
   

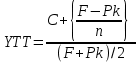, где С – годовой процентный купонный доход; Pk – текущий рыночный курс; F – номинал облигации; n – лет к погашению.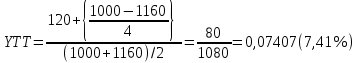


Задание 2

Допустим, вы купили корпоративную облигацию со сроком до погашения 10 лет, номиналом 1000 рублей и ставкой купона 8%, который выплачивается один раз в год. Сразу же после проведения вами этой операции, рыночные ставки возросли до 10%, и этот уровень зафиксирован.

Определите реализованную вами доходность, если вы продали эту облигацию 3 года спустя.
Решение:

Реализованная доходность – это норма прибыли, полученная инвестором
за период времени, меньший, чем срок действия выпуска.

Расчёт данного показателя ведётся по формуле:

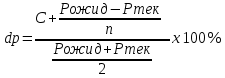, гдеС – годовой купонный доход; Рожид – ожидаемый будущий курс; Ртек – текущий рыночный курс; n – период владения облигацией.

1. 
   Определим ожидаемый будущий курс по формуле текущей стоимости облигации: ,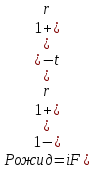
   где t – срок обращения облигации; F – номинальная цена облигации; r – годовые проценты по облигации; i – рыночная процентная ставка.
   

2. 
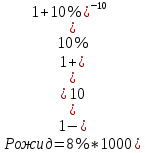
   Найдём годовой процентный купонный доход: С = 1000 * 8% = 80 руб.
   
3. 
   Облигация приобретена по номиналу, следовательно: Ртек = F = 1000 руб.
   
4. 
   Таким образом, реализованная доходность облигации составляет:
   

---

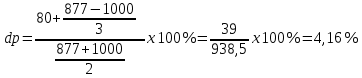
Задание 5

1000 рублевая облигация с 8-процентным купоном продаётся на рынке
с дисконтом в 10%, со сроком обращения 3 года. Определите текущую доходность облигации и доходность к погашению.
Решение:

1. 
   Текущая доходность определяется по формуле:
   

CY = 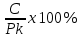, где: C – годовой процентный купонный доход; Pk - текущий рыночный курс.

Определим текущую цену облигации на рынке: Pk = 1000 – 10% = 900 руб.

Найдём годовой процентный купонный доход: С = 1000 * 8% = 80 руб.

Текущая доходность равна:

2. 
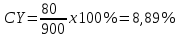
   Доходность к погашению определяется по формуле:
   

I = 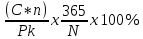, где C – годовой процентный купонный доход, Pk – текущий рыночный курс, n – срок обращения облигации, N – лет к погашению.

---

Смотрите также файлы

• 365стр. Проверь начало.docx

• Учебнометодическое пособие по дисциплине Введение в компьютерные технологии Москва Физический факультет мгу имени М. В. Ломоносова 2022.docx

• Новогодний праздник в старшей группе Снегурочка и бабаЯга Сигнал к началу праздника.docx

• Ситуационный практикум 1.docx

• Саба Балалар мен лкендер Сынып.docx