Файл: Отчет по лабораторной работе 1 по дисциплине Теория языков программирования и методы трансляции.docx
Добавлен: 29.04.2024
Просмотров: 33
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
C(n) (рис. 3).
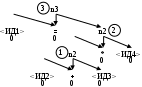
Рис. 3 – Дерево с уровнями
Уровни записываются для того, чтобы контролировать использование временных ячеек памяти. Две нужные нам величины нельзя заслать в одну и ту же ячейку памяти.
Теперь определим синтаксически управляемый алгоритм генерации кода, предназначенный для вычисления кода C(n) всех вершин дерева, состоящих из листьев корня типа «а» и внутренних вершин типа «б» и «в».
Алгоритм.
Вход. Помеченное упорядоченное дерево, представляющее собой оператор присвоения, включающий только арифметические операции «*» и «+». Предполагается, что уровни всех вершин уже вычислены.
Выход. Код в ячейке ассемблера, вычисляющий этот оператор присвоения.
Метод. Делать шаги 1) и 2) для всех вершин уровня 0, затем для вершин уровня 1 и т.д., пока не будут отработаны все вершины.
1) Пусть n – лист с меткой <ИДi>.
1.1. Допустим, что элемент i таблицы идентификаторов является переменной. Тогда C(n) – имя этой переменной.
1.2. Допустим, что элемент j таблицы идентификаторов является константой k, тогда C(n) – цепочка =k.
2) Если n – лист с меткой «=», «+» или «*», то C(n) – пустая цепочка.
3) Если n – вершина типа «а» и ее прямые потомки – это вершины n1, n2 и n3, то C(n) – цепочка LOAD C(n3); STORE C(n1).
4) Если n – вершина типа «б» и ее прямые потомки – это вершины n1, n2 и n3, то C(n) – цепочка C(n3); STORE $l(n); LOAD C(n1); ADD $l(n). Эта последовательность занимает временную ячейку, именем которой служит знак «$» вместе со следующим за ним уровнем вершины n. Непосредственно видно, что если перед этой последовательностью поставить LOAD, то значение, которое она поместит в сумматор, будет суммой значений выражений поддеревьев, над которыми доминируют вершины n1 и n3. Выбор имен временных ячеек гарантирует, что два нужных значения одновременно не появятся в одной ячейке.
5) Если n – вершина типа «в», а все остальное – как и в 4), то C(n) – цепочка C(n3); STORE $l(n); LOAD C(n1); MPY $l(n).
Применим этот алгоритм к нашему примеру (рис. 4).

Рис. 4 – Дерево с генерированными кодами
Таким образом, в корне мы получили программу на языке типа «ассемблер», эквивалентную исходному выражению.
Естественно, эта программа далека от оптимальной, но это можно исправить на этапе оптимизации.
Рассмотрим приемы, которые делают код более коротким:
1) Если «+» – коммутативная операция, то можно заменить последовательность команд LOAD α; ADD β; последовательностью LOAD β; ADD α. Требуется, однако, чтобы в других местах не было перехода к оператору
ADD β.
2) Подобным же образом, если «*» – коммутативная операция, то можно заменить LOAD α; MPY β; на LOAD β; MPY α.
3) Последовательность операторов типа STORE α; LOAD α; можно удалить из программы при условии, что или ячейка α не будет использоваться далее, или перед использованием ячейка α будет заполнена заново.
4) Последовательность LOAD α; STORE β; можно удалить, если за ней следует другой оператор LOAD и нет перехода к оператору STORE β, а последующие вхождения β будут заменены на α вплоть до того места, где появится другой оператор STORE γ.
Получим оптимизированную программу для нашего примера (табл. 3).
Таблица 3 – Оптимизация кода
Детерминированный конечный автомат с магазинной памятью (ДМП-автомат, или ДМПА) – это семерка
P = (Q, Σ, Γ, δ, q0, Z0, F),
где:
– Q – конечное множество символов состояния, представляющих всевозможные состояния управляющего устройства;
– Σ – конечный входной алфавит;
– Γ – конечный алфавит магазинных символов;
– δ – функция переходов, отображение множества Q×(Σ∪{e
}∪{⊥})×Γ во множество Q×Γ*;
– q0∈Q – начальное состояние управляющего устройства;
– Z0∈Γ – символ, находящийся в магазине в начальный момент (начальный символ);
– F⊆Q – множество заключительных состояний.
Конфигурацией ДМП-автомата P называется тройка (q, w, α)∈Q×Σ*×Γ*, где:
– q – текущее состояние устройства;
– w – неиспользованная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
– α – содержимое магазина; самый левый символ цепочки α считается верхним символом магазина; если α = e, то магазин считается пустым.
Здесь «⊥» – специальный маркер, обозначающий конец входной цепочки. То есть считаем, что на входе ДМПА находится символ «⊥», если вся входная цепочка прочитана (w = e).
Такт работы ДМП-автомата P будет представляться в виде бинарного отношения , определенного на конфигурациях. Будем писать
, определенного на конфигурациях. Будем писать
(q, aw, Zα) (q', w, γα),
(q', w, γα),
если функция переходов δ(q, a, Z) = (q', γ), где q, q'∈Q, a∈Σ∪{e}∪{⊥}, w∈Σ*, Z∈Γ, α, γ∈Γ*.
Если δ(q, a, Z) = (q', γ), то говорят о том, что ДМП-автомат P, находясь в состоянии q и имея a в качестве текущего входного символа, расположенного под входной головкой, а Z – в качестве верхнего символа магазина, может:
– перейти в состояние q';
– сдвинуть головку на одну ячейку вправо;
– заменить верхний символ магазина цепочкой γ магазинных символов.
Если Z = e, то символ из стека не удаляется, т.е. верхний символ магазина не принимается в расчет. Если γ = e, то верхний символ удаляется из магазина, тем самым магазинный список сокращается. Если a = e, будем называть этот такт e-тактом. В e - такте текущий входной символ не принимается во внимание и входная головка не сдвигается. Однако состояние управляющего устройства и содержимое памяти могут измениться.
Начальной конфигурацией ДМП-автомата P называется конфигурация вида (q0, w, Z0), где w∈Σ*, т.е. управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно распознать, и в магазине есть только начальный символ Z0. Заключительная конфигурация – это конфигурация вида (q, е, α), где q∈F и α∈Γ*.
Говорят, что цепочка w допускается ДМП-автоматом P, если (q0, w, Z0) ?* (q, е, α) для некоторых q∈F и α∈Γ*. А L(P) – т.е. язык, определяемый автоматом P, – это множество цепочек, допускаемых автоматом P.
В простейшем случае, когда ДМПА не использует стек, т.е. все его конфигурации имеют вид (q, w, e), он вырождается в обычный детерминированный конечный автомат (ДКА) M = (Q, Σ, δ, q0, F), где:
– Q – конечное множество состояний;
– Σ – конечное множество допустимых входных символов;
– δ – функция переходов, отображение множества Q×(Σ∪{⊥}) во множество Q;
– q0∈Q – начальное состояние управляющего устройства;
– F⊆Q – множество заключительных состояний.
То есть ДКА – это частный случай ДМПА.
Построенный автомат:
– Q –{ START, S1, S2, S3, S4, S5, S6, CH, CHS1, CHS2, CHS3, CHS3_, CHS4 CH1, CH1S1, CH1S2, CH1S3, CH1S3_, CH1S4, NUM, NUM2, NUME, NUME2,FINISH;
– Σ – –{ +-*=()_. [A-Z] [a-z] [0-9]};
– Γ –{ =(+*};
– δ –
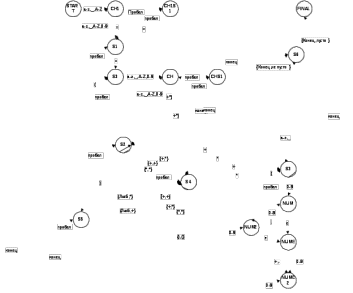
– q0∈Q – START;
– Z0∈Γ – Стек в начале пуст
– F⊆Q – FINISH.
Результаты работы программы:
COST=(PRICE+TAX)*0.98
Таблица имен
COST variable
PRICE variable
TAX variable
0.98 constant
Псевдопрограмма
1:load PRICE;
2:store $1;
3:load TAX;
4:add $1;
5:store $2;
6:load 0.98;
7:mpy $2;
8:store COST;
Псевдопрограмма после оптимизиции
1:load TAX;
2:add PRICE;
3:mpy 0.98;
4:store COST;
На языке C# разработана программа для разбора математического выражения и построения по нему псевдопрограммы. Дерево синтаксического разбора строится с помощью помощью ДМПА автомата.
1. Калайда В.Т., Романенко В.В. Теория языков программирования и методы трансляции: учебное пособие / В.Т. Калайда, В.В. Романенко. –Томск: ФДО, ТУСУР, 2019. – 219 с.
2. Калайда В. Т., Романенко В.В.Теория языков программирования и методы трансляции: учебное методическое пособие / В.Т. Калайда, В.В. Романенко. – Томск: ФДО, ТУСУР, 2019. – 125 с.
Приложение А
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
namespace W1
{
class Program
{
static class PsewdoProgram
{
static private List cmds;
static private List ops;
static public void PrepareProg()
{
cmds = new List();
ops = new List();
}
static public void AddCmd(String cmd, String operand)
{
cmds.Add(cmd);
ops.Add(operand);
}
static public void UpdOperand(string s)
{
ops[ops.Count - 1] = s;
}
static public void SaveProg(StreamWriter f)
{
for (int i = 0; i < cmds.Count; i++)
f.WriteLine("{2}:{0} {1};", cmds[i], ops[i], i + 1);
}
static public void SaveProg()
{
for (int i = 0; i < cmds.Count; i++)
Console.WriteLine("{2}:{0} {1};", cmds[i], ops[i], i + 1);
}
static private void optimize1()
{
for (int i = 0; i < cmds.Count() - 1; i++)
{
if (cmds[i] != "load") continue;
for (int j = i + 1; j < cmds.Count() - 1; j++)
{
if (cmds[j] != "add") break;
string tmp = ops[i];
ops[i] = ops[j];
ops[j] = tmp;
if (optimize3()) return;
break;
}
}
}
static private void optimize2()
{
for (int i = 0; i < cmds.Count() - 1; i++)
{
if (cmds[i] != "load") continue;
for (int j = i + 1; j < cmds.Count() - 1; j++)
{
if (cmds[j] != "mpy") break;
string tmp = ops[i];
ops[i] = ops[j];
ops[j] = tmp;
if (optimize3()) return;
break;
}
}
}
static private bool optimize3() //3е
{
for (int i = 0; i < cmds.Count() - 1; i++)
{
if (cmds[i] != "store") continue;
if (cmds[i + 1] != "load") continue;
if (ops[i] != ops[i + 1]) continue;
cmds.RemoveAt(i); ops.RemoveAt(i);
cmds.RemoveAt(i); ops.RemoveAt(i);
SaveProg();
return true;
}
return false;
}
static private void optimize4() // 4
{
for (int i = 0; i < cmds.Count() - 3; i++)
{
if (cmds[i] != "load") continue;
if (cmds[i + 1] != "store") continue;
if (cmds[i + 2] != "load") continue;
for (int j = i + 3; j < cmds.Count(); j++)
{
if (ops[i + 1] == ops[j])
if (cmds[j] == "store") break;
else
{
ops[j] = ops[i];
}
}
cmds.RemoveAt(i); ops.RemoveAt(i);
cmds.RemoveAt(i); ops.RemoveAt(i);
SaveProg();
return;
}
}
static public void OptimizeAll()
{
while (true)
{
SaveProg();
int l = cmds.Count;
optimize1();
optimize2();
optimize3();
optimize4();
if (l == cmds.Count) break;
}
}
}
class Tree
{
private string node;
private Tree left, right;
public Tree(string str, Tree l, Tree r)
{
node = str;
left = l;
right = r;
}
public void BuildProg()
{
if (node == "=")
{
PsewdoProgram.AddCmd("load", "");
right.BuildProg();
PsewdoProgram.AddCmd("store", left.node);
return;
}
if (node == "+" || node == "*")
{
right.BuildProg();
PsewdoProgram.AddCmd("store", string.Format("${0}", MaxLengthToTerm()));
PsewdoProgram.AddCmd("load", "");
left.BuildProg();
PsewdoProgram.AddCmd(node == "*" ? "mpy" : "add", string.Format("${0}", MaxLengthToTerm()));
return;
}
PsewdoProgram.UpdOperand(node);
}
private int MaxLengthToTerm()
{
if (left == null) return 0;
int l = left.MaxLengthToTerm();
int r = right.MaxLengthToTerm();
return 1 + (l > r ? l : r);
}
}
class RobotDMPA
{
private string[,] dmpa_rules;
private List stack = new List();
private Dictionary> tablenames = new Dictionary>();
private List inputchars = new List();
private int inputindex;
private List T = new List();
public RobotDMPA()
{
dmpa_rules = new string[,] {
{"START", "[A-Z]", "", "ADDCHAR", "CH1", "y"},
{"START", "[a-z]", "", "ADDCHAR", "CH1", "y"},
{"START", "_", "", "ADDCHAR", "CH1", "y"},
{"CH1", "[A-Z]", "", "ADDCHAR", "CH1", "y"},
{"CH1", "[a-z]", "", "ADDCHAR", "CH1", "y"},
{"CH1", "_", "", "ADDCHAR", "CH1", "y"},
{"CH1", "[0-9]", "", "ADDCHAR", "CH1", "y"},
{"CH1", " ", "", "FIXNAME", "CH1S1", "n"},
{"CH1", "=", "", "FIXNAME", "S1", "n"},
{"CH1S1", " ", "", "", "CH1S1","y"},
{"CH1S1", "=", "", "", "S1", "n"},
{"S1", " ", "", "", "S1", "y"},
{"S1", "=", "", "A2", "S3", "y"},
{"S2", " ", "", "", "S2", "y"},
{"S2", "", "", "", "S6", "n"},
{"S2", "+", "+", "A3", "S4", "n"},
{"S2", "+", "*", "A4", "S4", "n"},
{"S2", "+", "", "A2", "S3", "y"},
{"S2", "*", "*", "A3", "S4", "n"},
{"S2", "*", "", "A2", "S3", "y"},
{"S2", ")", "", "", "S5", "n"},
{"S3", "(", "", "A2", "S3", "y"},
{"S3", " ", "", "", "S3", "y"},
{"S3", "[A-Z]","", "ADDCHAR", "CH", "y"},
{"S3", "[a-z]","", "ADDCHAR", "CH", "y"},
{"S3", "_","", "ADDCHAR", "CH", "y"},
{"S3", "[0-9]","", "ADDCHAR", "NUM", "y"},
{"CH", "[A-Z]", "", "ADDCHAR", "CH", "y"},
{"CH", "[a-z]", "", "ADDCHAR", "CH", "y"},
{"CH", "_", "", "ADDCHAR", "CH", "y"},
{"CH", "[0-9]", "", "ADDCHAR", "CH", "y"},
{"CH", " ", "", "FIXNAME", "CHS1", "n"},
{"CH", "+", "", "FIXNAME", "S2", "n"},
{"CH", "*", "", "FIXNAME", "S2", "n"},
{"CH", ")", "", "FIXNAME", "S2", "n"},
{"CH", "", "", "FIXNAME", "S6", "n"},
{"CHS1", " ", "", "", "CHS1","y"},
{"CHS1", "+", "", "", "S2", "n"},
{"CHS1", "*", "", "", "S2", "n"},
{"CHS1", ")", "", "", "S2", "n"},
{"CHS1", "", "", "", "S2", "n"},
{"CHS2", " ", "", "", "CHS2","y"},
{"S4", " ", " ", "", "S4", "y"},
{"S4", "+", "+", "A3", "S4", "n"},
{"S4", "+", "*", "A4", "S4", "n"},
{"S4", "+", "", "A2", "S3", "y"},
{"S4", "*", "*", "A4", "S4", "n"},
{"S4", "*", "", "A2", "S3", "y"},
{"S5", " ", " ", "", "S5", "y"},
{"S5", ")", "(", "A5", "S2", "y"},
{"S5", "", "+", "A4", "S5", "n"},
{"S5", "", "*", "A4", "S5", "n"},
{"S6", "", "", "A4", "S6", "n"},
{"S6", "", "", "", "FINAL", "n"},
{"NUM", "[0-9]", "", "ADDCHAR", "NUM", "y"},
{"NUM", "E", "", "ADDCHAR", "NUME", "y"},
{"NUM", "e", "", "ADDCHAR", "NUME", "y"},
{"NUM", ".", "", "ADDCHAR", "NUM2", "y"},
{"NUM", "", "", "FIXNAME", "S2", "n"},
{"NUM2", "[0-9]", "", "ADDCHAR", "NUM2", "y"},
{"NUM2", "E", "", "ADDCHAR", "NUME", "y"},
{"NUM2", "e", "", "ADDCHAR", "NUME", "y"},
{"NUM2", "", "", "FIXNAME", "S2", "n"},
{"NUME", "+", "", "ADDCHAR", "NUME2", "y"},
{"NUME", "-", "", "ADDCHAR", "NUME2", "y"},
{"NUME", "[0-9]", "", "ADDCHAR", "NUME2", "y"},
{"NUME2", "[0-9]", "", "ADDCHAR", "NUME2", "y"},
{"NUME2", "", "", "FIXNAME", "S2", "n"},
{"", "", "", "", "", ""}};
}
private void loadfile(string fn)
{
string s = File.ReadAllText(fn);
string spaces = " \n\r\t";
foreach (char ch in s)
{
if (spaces.IndexOf(ch) == -1) inputchars.Add(ch);
else inputchars.Add(' ');
}
inputindex = 0;
}
public Tree BuildTree()
{
loadfile("Input.txt");
int i = 0;
string ch;
bool end = inputindex >= inputchars.Count;
char lex = inputchars[inputindex];
string buf = "";
string lastname = "";
string DMPState = "START";
while (DMPState != "FINAL")
{
i = 0;
while (dmpa_rules[i, 0] != "")
{
ch = dmpa_rules[i, 0];
if (ch != DMPState) { i++; continue; }
ch = dmpa_rules[i, 1];
bool fnd = ch == "";
if (!fnd)
{
if (ch.Length == 5 && ch[0] == '[' && ch[1] <= lex
&& ch[2] == '-' && ch[3] >= lex && ch[4] == ']') fnd = true;
if (ch == "" && end) fnd = true;
if (!fnd && ch[0] == lex) fnd = true;
}
ch = dmpa_rules[i, 2];
bool stok = ch == "";
if (!stok)
{
if (ch == "" && stack.Count == 0) stok = true;
if (ch == "" && stack.Count > 0) stok = true;
if (ch[0] != '<' && ch == stack[stack.Count - 1]) stok = true;
}
if (fnd && stok) break;
i++;
}
if (dmpa_rules[i, 0] == "") break;
ch = dmpa_rules[i, 3];
if (ch != "")
{
if (ch == "ADDCHAR")
{
buf += lex;
}
if (ch == "FIXNAME")
{
tores(buf);
lastname = buf;
buf = "";
}
if (ch == "A1")
{
tores(lex.ToString());
}
if (ch == "A2")
{
stack.Add(lex.ToString());
}
if (ch == "A3")
{
tores(lex.ToString());
stack.RemoveAt(stack.Count - 1);
}
if (ch == "A4")
{
tores(stack[stack.Count - 1]);
stack.RemoveAt(stack.Count - 1);
}
if (ch == "A5")
{
stack.RemoveAt(stack.Count - 1);
}
}
DMPState = dmpa_rules[i, 4];
if (dmpa_rules[i, 5] == "y")
{
inputindex++;
end = inputindex >= inputchars.Count;
lex = end ? '\0' : inputchars[inputindex];
}
}
return DMPState == "FINAL" ? T[0] : null;
}
private void tores(string lex)
{
if (lex == "=")
{
Tree r = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
Tree l = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
T.Add(new Tree("=", l, r));
return;
}
if (lex == "+")
{
Tree l = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
Tree r = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
T.Add(new Tree("+", l, r));
return;
}
if (lex == "*")
{
Tree l = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
Tree r = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
T.Add(new Tree("*", l, r));
return;
}
T.Add(new Tree(lex, null, null));
if (!tablenames.ContainsKey(lex)) tablenames.Add(lex, new List());
}
public void SaveTable(StreamWriter file)
{
foreach (KeyValuePair> k in tablenames)
{
if (k.Key[0] >= '0' && k.Key[0] <= '9') file.WriteLine("{0} constant", k.Key);
else
{
string s = k.Key;
foreach (int j in k.Value)
s += string.Format("[{0}]", j);
file.WriteLine("{0} variable", s);
}
}
}
}
static void Main(string[] args)
{
StreamWriter f = new StreamWriter("Output.txt");
f.AutoFlush = true;
RobotDMPA dmpa = new RobotDMPA();
PsewdoProgram.PrepareProg();
Tree t = dmpa.BuildTree();
if (t != null)
{
f.WriteLine("Таблица имен");
dmpa.SaveTable(f);
t.BuildProg();
f.WriteLine("Псевдопрограмма");
PsewdoProgram.SaveProg(f);
PsewdoProgram.OptimizeAll();
f.WriteLine("Псевдопрограмма после оптимизиции");
PsewdoProgram.SaveProg(f);
}
else f.WriteLine("Ошибка во входном выражении");
}
}
}

Рис. 3 – Дерево с уровнями
Уровни записываются для того, чтобы контролировать использование временных ячеек памяти. Две нужные нам величины нельзя заслать в одну и ту же ячейку памяти.
Теперь определим синтаксически управляемый алгоритм генерации кода, предназначенный для вычисления кода C(n) всех вершин дерева, состоящих из листьев корня типа «а» и внутренних вершин типа «б» и «в».
Алгоритм.
Вход. Помеченное упорядоченное дерево, представляющее собой оператор присвоения, включающий только арифметические операции «*» и «+». Предполагается, что уровни всех вершин уже вычислены.
Выход. Код в ячейке ассемблера, вычисляющий этот оператор присвоения.
Метод. Делать шаги 1) и 2) для всех вершин уровня 0, затем для вершин уровня 1 и т.д., пока не будут отработаны все вершины.
1) Пусть n – лист с меткой <ИДi>.
1.1. Допустим, что элемент i таблицы идентификаторов является переменной. Тогда C(n) – имя этой переменной.
1.2. Допустим, что элемент j таблицы идентификаторов является константой k, тогда C(n) – цепочка =k.
2) Если n – лист с меткой «=», «+» или «*», то C(n) – пустая цепочка.
3) Если n – вершина типа «а» и ее прямые потомки – это вершины n1, n2 и n3, то C(n) – цепочка LOAD C(n3); STORE C(n1).
4) Если n – вершина типа «б» и ее прямые потомки – это вершины n1, n2 и n3, то C(n) – цепочка C(n3); STORE $l(n); LOAD C(n1); ADD $l(n). Эта последовательность занимает временную ячейку, именем которой служит знак «$» вместе со следующим за ним уровнем вершины n. Непосредственно видно, что если перед этой последовательностью поставить LOAD, то значение, которое она поместит в сумматор, будет суммой значений выражений поддеревьев, над которыми доминируют вершины n1 и n3. Выбор имен временных ячеек гарантирует, что два нужных значения одновременно не появятся в одной ячейке.
5) Если n – вершина типа «в», а все остальное – как и в 4), то C(n) – цепочка C(n3); STORE $l(n); LOAD C(n1); MPY $l(n).
Применим этот алгоритм к нашему примеру (рис. 4).

Рис. 4 – Дерево с генерированными кодами
Таким образом, в корне мы получили программу на языке типа «ассемблер», эквивалентную исходному выражению.
Естественно, эта программа далека от оптимальной, но это можно исправить на этапе оптимизации.
2.5 Оптимизация кода
Рассмотрим приемы, которые делают код более коротким:
1) Если «+» – коммутативная операция, то можно заменить последовательность команд LOAD α; ADD β; последовательностью LOAD β; ADD α. Требуется, однако, чтобы в других местах не было перехода к оператору
ADD β.
2) Подобным же образом, если «*» – коммутативная операция, то можно заменить LOAD α; MPY β; на LOAD β; MPY α.
3) Последовательность операторов типа STORE α; LOAD α; можно удалить из программы при условии, что или ячейка α не будет использоваться далее, или перед использованием ячейка α будет заполнена заново.
4) Последовательность LOAD α; STORE β; можно удалить, если за ней следует другой оператор LOAD и нет перехода к оператору STORE β, а последующие вхождения β будут заменены на α вплоть до того места, где появится другой оператор STORE γ.
Получим оптимизированную программу для нашего примера (табл. 3).
Таблица 3 – Оптимизация кода
| | | | |
| Этап 1 | Этап 2 | Этап 3 | |
| Применяем правило 1 к последовательности LOAD PRICE ADD $1 Заменяем ее последовательностью LOAD $1 ADD PRICE | Применяем правило 3 и удаляем последовательность STORE $1 LOAD $1 | К последовательности LOAD =0.98 STORE $2 применяем правило 4 и удаляем ее. В команде MPY $2 заменяем $2 на =0.98 | |
| LOAD =0.98 STORE $2 LOAD TAX STORE $1 LOAD $1 ADD PRICE MPY $2 STORE COST | LOAD =0.98 STORE $2 LOAD TAX ADD PRICE MPY $2 STORE COST | LOAD TAX ADD PRICE MPY =0.98 STORE COST | |
2.6 ДМП автомат
Детерминированный конечный автомат с магазинной памятью (ДМП-автомат, или ДМПА) – это семерка
P = (Q, Σ, Γ, δ, q0, Z0, F),
где:
– Q – конечное множество символов состояния, представляющих всевозможные состояния управляющего устройства;
– Σ – конечный входной алфавит;
– Γ – конечный алфавит магазинных символов;
– δ – функция переходов, отображение множества Q×(Σ∪{e
}∪{⊥})×Γ во множество Q×Γ*;
– q0∈Q – начальное состояние управляющего устройства;
– Z0∈Γ – символ, находящийся в магазине в начальный момент (начальный символ);
– F⊆Q – множество заключительных состояний.
Конфигурацией ДМП-автомата P называется тройка (q, w, α)∈Q×Σ*×Γ*, где:
– q – текущее состояние устройства;
– w – неиспользованная часть входной цепочки; первый символ цепочки w находится под входной головкой; если w = e, то считается, что вся входная лента прочитана;
– α – содержимое магазина; самый левый символ цепочки α считается верхним символом магазина; если α = e, то магазин считается пустым.
Здесь «⊥» – специальный маркер, обозначающий конец входной цепочки. То есть считаем, что на входе ДМПА находится символ «⊥», если вся входная цепочка прочитана (w = e).
Такт работы ДМП-автомата P будет представляться в виде бинарного отношения
 , определенного на конфигурациях. Будем писать
, определенного на конфигурациях. Будем писать(q, aw, Zα)
 (q', w, γα),
(q', w, γα),если функция переходов δ(q, a, Z) = (q', γ), где q, q'∈Q, a∈Σ∪{e}∪{⊥}, w∈Σ*, Z∈Γ, α, γ∈Γ*.
Если δ(q, a, Z) = (q', γ), то говорят о том, что ДМП-автомат P, находясь в состоянии q и имея a в качестве текущего входного символа, расположенного под входной головкой, а Z – в качестве верхнего символа магазина, может:
– перейти в состояние q';
– сдвинуть головку на одну ячейку вправо;
– заменить верхний символ магазина цепочкой γ магазинных символов.
Если Z = e, то символ из стека не удаляется, т.е. верхний символ магазина не принимается в расчет. Если γ = e, то верхний символ удаляется из магазина, тем самым магазинный список сокращается. Если a = e, будем называть этот такт e-тактом. В e - такте текущий входной символ не принимается во внимание и входная головка не сдвигается. Однако состояние управляющего устройства и содержимое памяти могут измениться.
Начальной конфигурацией ДМП-автомата P называется конфигурация вида (q0, w, Z0), где w∈Σ*, т.е. управляющее устройство находится в начальном состоянии, входная лента содержит цепочку, которую нужно распознать, и в магазине есть только начальный символ Z0. Заключительная конфигурация – это конфигурация вида (q, е, α), где q∈F и α∈Γ*.
Говорят, что цепочка w допускается ДМП-автоматом P, если (q0, w, Z0) ?* (q, е, α) для некоторых q∈F и α∈Γ*. А L(P) – т.е. язык, определяемый автоматом P, – это множество цепочек, допускаемых автоматом P.
В простейшем случае, когда ДМПА не использует стек, т.е. все его конфигурации имеют вид (q, w, e), он вырождается в обычный детерминированный конечный автомат (ДКА) M = (Q, Σ, δ, q0, F), где:
– Q – конечное множество состояний;
– Σ – конечное множество допустимых входных символов;
– δ – функция переходов, отображение множества Q×(Σ∪{⊥}) во множество Q;
– q0∈Q – начальное состояние управляющего устройства;
– F⊆Q – множество заключительных состояний.
То есть ДКА – это частный случай ДМПА.
3 Результаты работы
Построенный автомат:
– Q –{ START, S1, S2, S3, S4, S5, S6, CH, CHS1, CHS2, CHS3, CHS3_, CHS4 CH1, CH1S1, CH1S2, CH1S3, CH1S3_, CH1S4, NUM, NUM2, NUME, NUME2,FINISH;
– Σ – –{ +-*=()_. [A-Z] [a-z] [0-9]};
– Γ –{ =(+*};
– δ –

– q0∈Q – START;
– Z0∈Γ – Стек в начале пуст
– F⊆Q – FINISH.
Результаты работы программы:
COST=(PRICE+TAX)*0.98
Таблица имен
COST variable
PRICE variable
TAX variable
0.98 constant
Псевдопрограмма
1:load PRICE;
2:store $1;
3:load TAX;
4:add $1;
5:store $2;
6:load 0.98;
7:mpy $2;
8:store COST;
Псевдопрограмма после оптимизиции
1:load TAX;
2:add PRICE;
3:mpy 0.98;
4:store COST;
4 Выводы
На языке C# разработана программа для разбора математического выражения и построения по нему псевдопрограммы. Дерево синтаксического разбора строится с помощью помощью ДМПА автомата.
Список литературы
1. Калайда В.Т., Романенко В.В. Теория языков программирования и методы трансляции: учебное пособие / В.Т. Калайда, В.В. Романенко. –Томск: ФДО, ТУСУР, 2019. – 219 с.
2. Калайда В. Т., Романенко В.В.Теория языков программирования и методы трансляции: учебное методическое пособие / В.Т. Калайда, В.В. Романенко. – Томск: ФДО, ТУСУР, 2019. – 125 с.
Приложение А
(справочное)
Листинг программы
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.IO;
namespace W1
{
class Program
{
static class PsewdoProgram
{
static private List
static private List
static public void PrepareProg()
{
cmds = new List
ops = new List
}
static public void AddCmd(String cmd, String operand)
{
cmds.Add(cmd);
ops.Add(operand);
}
static public void UpdOperand(string s)
{
ops[ops.Count - 1] = s;
}
static public void SaveProg(StreamWriter f)
{
for (int i = 0; i < cmds.Count; i++)
f.WriteLine("{2}:{0} {1};", cmds[i], ops[i], i + 1);
}
static public void SaveProg()
{
for (int i = 0; i < cmds.Count; i++)
Console.WriteLine("{2}:{0} {1};", cmds[i], ops[i], i + 1);
}
static private void optimize1()
{
for (int i = 0; i < cmds.Count() - 1; i++)
{
if (cmds[i] != "load") continue;
for (int j = i + 1; j < cmds.Count() - 1; j++)
{
if (cmds[j] != "add") break;
string tmp = ops[i];
ops[i] = ops[j];
ops[j] = tmp;
if (optimize3()) return;
break;
}
}
}
static private void optimize2()
{
for (int i = 0; i < cmds.Count() - 1; i++)
{
if (cmds[i] != "load") continue;
for (int j = i + 1; j < cmds.Count() - 1; j++)
{
if (cmds[j] != "mpy") break;
string tmp = ops[i];
ops[i] = ops[j];
ops[j] = tmp;
if (optimize3()) return;
break;
}
}
}
static private bool optimize3() //3е
{
for (int i = 0; i < cmds.Count() - 1; i++)
{
if (cmds[i] != "store") continue;
if (cmds[i + 1] != "load") continue;
if (ops[i] != ops[i + 1]) continue;
cmds.RemoveAt(i); ops.RemoveAt(i);
cmds.RemoveAt(i); ops.RemoveAt(i);
SaveProg();
return true;
}
return false;
}
static private void optimize4() // 4
{
for (int i = 0; i < cmds.Count() - 3; i++)
{
if (cmds[i] != "load") continue;
if (cmds[i + 1] != "store") continue;
if (cmds[i + 2] != "load") continue;
for (int j = i + 3; j < cmds.Count(); j++)
{
if (ops[i + 1] == ops[j])
if (cmds[j] == "store") break;
else
{
ops[j] = ops[i];
}
}
cmds.RemoveAt(i); ops.RemoveAt(i);
cmds.RemoveAt(i); ops.RemoveAt(i);
SaveProg();
return;
}
}
static public void OptimizeAll()
{
while (true)
{
SaveProg();
int l = cmds.Count;
optimize1();
optimize2();
optimize3();
optimize4();
if (l == cmds.Count) break;
}
}
}
class Tree
{
private string node;
private Tree left, right;
public Tree(string str, Tree l, Tree r)
{
node = str;
left = l;
right = r;
}
public void BuildProg()
{
if (node == "=")
{
PsewdoProgram.AddCmd("load", "");
right.BuildProg();
PsewdoProgram.AddCmd("store", left.node);
return;
}
if (node == "+" || node == "*")
{
right.BuildProg();
PsewdoProgram.AddCmd("store", string.Format("${0}", MaxLengthToTerm()));
PsewdoProgram.AddCmd("load", "");
left.BuildProg();
PsewdoProgram.AddCmd(node == "*" ? "mpy" : "add", string.Format("${0}", MaxLengthToTerm()));
return;
}
PsewdoProgram.UpdOperand(node);
}
private int MaxLengthToTerm()
{
if (left == null) return 0;
int l = left.MaxLengthToTerm();
int r = right.MaxLengthToTerm();
return 1 + (l > r ? l : r);
}
}
class RobotDMPA
{
private string[,] dmpa_rules;
private List
private Dictionary
private List
private int inputindex;
private List
public RobotDMPA()
{
dmpa_rules = new string[,] {
{"START", "[A-Z]", "", "ADDCHAR", "CH1", "y"},
{"START", "[a-z]", "", "ADDCHAR", "CH1", "y"},
{"START", "_", "", "ADDCHAR", "CH1", "y"},
{"CH1", "[A-Z]", "", "ADDCHAR", "CH1", "y"},
{"CH1", "[a-z]", "", "ADDCHAR", "CH1", "y"},
{"CH1", "_", "", "ADDCHAR", "CH1", "y"},
{"CH1", "[0-9]", "", "ADDCHAR", "CH1", "y"},
{"CH1", " ", "", "FIXNAME", "CH1S1", "n"},
{"CH1", "=", "", "FIXNAME", "S1", "n"},
{"CH1S1", " ", "", "", "CH1S1","y"},
{"CH1S1", "=", "", "", "S1", "n"},
{"S1", " ", "", "", "S1", "y"},
{"S1", "=", "", "A2", "S3", "y"},
{"S2", " ", "", "", "S2", "y"},
{"S2", "
{"S2", "+", "+", "A3", "S4", "n"},
{"S2", "+", "*", "A4", "S4", "n"},
{"S2", "+", "", "A2", "S3", "y"},
{"S2", "*", "*", "A3", "S4", "n"},
{"S2", "*", "", "A2", "S3", "y"},
{"S2", ")", "", "", "S5", "n"},
{"S3", "(", "", "A2", "S3", "y"},
{"S3", " ", "", "", "S3", "y"},
{"S3", "[A-Z]","", "ADDCHAR", "CH", "y"},
{"S3", "[a-z]","", "ADDCHAR", "CH", "y"},
{"S3", "_","", "ADDCHAR", "CH", "y"},
{"S3", "[0-9]","", "ADDCHAR", "NUM", "y"},
{"CH", "[A-Z]", "", "ADDCHAR", "CH", "y"},
{"CH", "[a-z]", "", "ADDCHAR", "CH", "y"},
{"CH", "_", "", "ADDCHAR", "CH", "y"},
{"CH", "[0-9]", "", "ADDCHAR", "CH", "y"},
{"CH", " ", "", "FIXNAME", "CHS1", "n"},
{"CH", "+", "", "FIXNAME", "S2", "n"},
{"CH", "*", "", "FIXNAME", "S2", "n"},
{"CH", ")", "", "FIXNAME", "S2", "n"},
{"CH", "
{"CHS1", " ", "", "", "CHS1","y"},
{"CHS1", "+", "", "", "S2", "n"},
{"CHS1", "*", "", "", "S2", "n"},
{"CHS1", ")", "", "", "S2", "n"},
{"CHS1", "
{"CHS2", " ", "", "", "CHS2","y"},
{"S4", " ", " ", "", "S4", "y"},
{"S4", "+", "+", "A3", "S4", "n"},
{"S4", "+", "*", "A4", "S4", "n"},
{"S4", "+", "", "A2", "S3", "y"},
{"S4", "*", "*", "A4", "S4", "n"},
{"S4", "*", "", "A2", "S3", "y"},
{"S5", " ", " ", "", "S5", "y"},
{"S5", ")", "(", "A5", "S2", "y"},
{"S5", "", "+", "A4", "S5", "n"},
{"S5", "", "*", "A4", "S5", "n"},
{"S6", "
{"S6", "
{"NUM", "[0-9]", "", "ADDCHAR", "NUM", "y"},
{"NUM", "E", "", "ADDCHAR", "NUME", "y"},
{"NUM", "e", "", "ADDCHAR", "NUME", "y"},
{"NUM", ".", "", "ADDCHAR", "NUM2", "y"},
{"NUM", "", "", "FIXNAME", "S2", "n"},
{"NUM2", "[0-9]", "", "ADDCHAR", "NUM2", "y"},
{"NUM2", "E", "", "ADDCHAR", "NUME", "y"},
{"NUM2", "e", "", "ADDCHAR", "NUME", "y"},
{"NUM2", "", "", "FIXNAME", "S2", "n"},
{"NUME", "+", "", "ADDCHAR", "NUME2", "y"},
{"NUME", "-", "", "ADDCHAR", "NUME2", "y"},
{"NUME", "[0-9]", "", "ADDCHAR", "NUME2", "y"},
{"NUME2", "[0-9]", "", "ADDCHAR", "NUME2", "y"},
{"NUME2", "", "", "FIXNAME", "S2", "n"},
{"", "", "", "", "", ""}};
}
private void loadfile(string fn)
{
string s = File.ReadAllText(fn);
string spaces = " \n\r\t";
foreach (char ch in s)
{
if (spaces.IndexOf(ch) == -1) inputchars.Add(ch);
else inputchars.Add(' ');
}
inputindex = 0;
}
public Tree BuildTree()
{
loadfile("Input.txt");
int i = 0;
string ch;
bool end = inputindex >= inputchars.Count;
char lex = inputchars[inputindex];
string buf = "";
string lastname = "";
string DMPState = "START";
while (DMPState != "FINAL")
{
i = 0;
while (dmpa_rules[i, 0] != "")
{
ch = dmpa_rules[i, 0];
if (ch != DMPState) { i++; continue; }
ch = dmpa_rules[i, 1];
bool fnd = ch == "";
if (!fnd)
{
if (ch.Length == 5 && ch[0] == '[' && ch[1] <= lex
&& ch[2] == '-' && ch[3] >= lex && ch[4] == ']') fnd = true;
if (ch == "
if (!fnd && ch[0] == lex) fnd = true;
}
ch = dmpa_rules[i, 2];
bool stok = ch == "";
if (!stok)
{
if (ch == "
if (ch == "
if (ch[0] != '<' && ch == stack[stack.Count - 1]) stok = true;
}
if (fnd && stok) break;
i++;
}
if (dmpa_rules[i, 0] == "") break;
ch = dmpa_rules[i, 3];
if (ch != "")
{
if (ch == "ADDCHAR")
{
buf += lex;
}
if (ch == "FIXNAME")
{
tores(buf);
lastname = buf;
buf = "";
}
if (ch == "A1")
{
tores(lex.ToString());
}
if (ch == "A2")
{
stack.Add(lex.ToString());
}
if (ch == "A3")
{
tores(lex.ToString());
stack.RemoveAt(stack.Count - 1);
}
if (ch == "A4")
{
tores(stack[stack.Count - 1]);
stack.RemoveAt(stack.Count - 1);
}
if (ch == "A5")
{
stack.RemoveAt(stack.Count - 1);
}
}
DMPState = dmpa_rules[i, 4];
if (dmpa_rules[i, 5] == "y")
{
inputindex++;
end = inputindex >= inputchars.Count;
lex = end ? '\0' : inputchars[inputindex];
}
}
return DMPState == "FINAL" ? T[0] : null;
}
private void tores(string lex)
{
if (lex == "=")
{
Tree r = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
Tree l = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
T.Add(new Tree("=", l, r));
return;
}
if (lex == "+")
{
Tree l = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
Tree r = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
T.Add(new Tree("+", l, r));
return;
}
if (lex == "*")
{
Tree l = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
Tree r = T[T.Count - 1];
T.RemoveAt(T.Count - 1);
T.Add(new Tree("*", l, r));
return;
}
T.Add(new Tree(lex, null, null));
if (!tablenames.ContainsKey(lex)) tablenames.Add(lex, new List
}
public void SaveTable(StreamWriter file)
{
foreach (KeyValuePair
{
if (k.Key[0] >= '0' && k.Key[0] <= '9') file.WriteLine("{0} constant", k.Key);
else
{
string s = k.Key;
foreach (int j in k.Value)
s += string.Format("[{0}]", j);
file.WriteLine("{0} variable", s);
}
}
}
}
static void Main(string[] args)
{
StreamWriter f = new StreamWriter("Output.txt");
f.AutoFlush = true;
RobotDMPA dmpa = new RobotDMPA();
PsewdoProgram.PrepareProg();
Tree t = dmpa.BuildTree();
if (t != null)
{
f.WriteLine("Таблица имен");
dmpa.SaveTable(f);
t.BuildProg();
f.WriteLine("Псевдопрограмма");
PsewdoProgram.SaveProg(f);
PsewdoProgram.OptimizeAll();
f.WriteLine("Псевдопрограмма после оптимизиции");
PsewdoProgram.SaveProg(f);
}
else f.WriteLine("Ошибка во входном выражении");
}
}
}

