Файл: Задача 1 Умножить в двоичной арифметике числа a и b.docx
Добавлен: 29.04.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа по Информатике
Вариант №3
Выполнил: Филатов Алексей Сергеевич
Задача № 1:
Умножить в двоичной арифметике числа a и b.
Умножение начинаем с младших разрядов: если текущий разряд второго числа равен 0, то везде записываем нули, если 1 - то переписываем первое число.
a = 1010, 101 b= 11, 1
1) 1 0 1 0
1 1
= = = = =
1 0 1 0
1 0 1 0
1 1 1 1 0
2) 1 0 1
1
1 0 1
Ответ:
1)1010*11 = 11110
2)101*1 = 101
Задача № 2:
Перевести число a из десятичной в систему счисления по основанию 4
A=4,5625
Целая часть числа находится делением на основание новой
4/4 = 1 и 4-4=0 -> 410 = 104
Дробная часть числа находится умножением на основание новой
5625*4 = 2,25 ->2
25*4 =100 ->1
Ответ: 10.21
Задача № 3:
Перевести число a из двоичной в десятичную систему счисления.
a=1001,1(011)
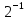* 0, (011) +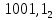 
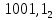
= 9.5
/
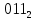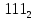= 3/7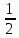
+ 
*
= + 
= 
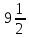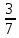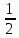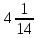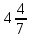= 4.57Ответ: 4.57
Задача № 4:
Перевести число а из восьмеричной в шестнадцатиричную систему счисления.
a=706,21
Переведем число в 10-ю систему счисления
706.218 = 7∙82+0∙81+6∙80+2∙8-1+1∙8-2 = 448+0+6+0.25+0.015625 = 454.26562510
Переведем 454.26562510 в шестнадцатиричную систему
Целая часть находится делением на основание новой
454/16 = 28 -> остаток от деления 6
28/16 = 1 -> остаток от деления 12 = С
Получилось
= 
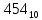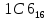
Дробная часть находится умножением на основание новой
0,265625*16 = 4,25 -> 4
0,25 * 16 = 4
Получилось
= 
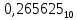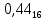
Ответ:
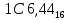
Задача № 5:
Даны десятичные коды символов из таблицы ASCII (для удобочитаемости коды символов разделены дефисом). Определить закодированный текст.
83-72-65-82-75
Ответ: S-H-A-R-K (Акула)
Задача № 6:
Записать текст шестнадцатеричными кодами таблицы ASCII.
SAILOR
Вначале преобразуем буквы в 10 систему по таблице ASCII:
83-65-73-76-79-82
Далее переведем 10ю в 16ю
Ответ : 53-41-49-4С-4F-52
Задача № 7:
Вычислить a + b. Оба числа записать как двоичные целые со знаком в 6-ти разрядной ячейке памяти. Результат перевести из двоичного в десятичный вид
a= –14
b=9
Переводим -14 в двоичную систему счисления
= 
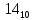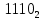-> 001110 тк 6ти разрядная ячейка -> инвертируем результат110001 и прибавляем 1 тк число отрицательное ->110010 результат
= 
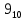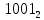-> 001001 тк 6ти разрядная ячейка110010 + 001001 = 111011
Отнимаем от младшего разряда 1 -> 111010 тк первое первый бит 1 значит число отрицательное.
Инвертируем 111010 -> 000101
= 
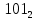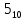
Т.к как число отрицательное
Ответ : -5
Задача № 8:
Вычислить a –b. Применить алгоритм компьютерного вычитания вещественных чисел. Длина мантиссы равна 6 разрядам.
a=
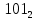
b=
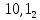
Сначала оба числа нормализуем:
a= 0.101 *
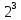
b= 0.101*
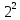
a-b = 0.101*
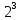- 0.101*
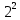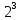= *(0.101 - 0.101*
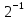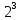)= *(0.101-0.0101)Выполним вычитание мантисс:
0.1010 - 0.0101 = 0.0101
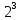*0.0101 = 10.1 -> если перевести в 10ю систему 2,5.Ответ : 10.1
Задача № 9:
Вычислить a x b. Применить алгоритм компьютерного умножения вещественных чисел. Длина мантиссы равна 6 разрядам. Результат перевести в 10-е число и сравнить с точным значением.
a= 1.001
b= 11.1
Сначала оба числа нормализуем:
a=0.1001*
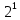
b=0.1110*
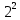
a*b = (0.1001 * 0.1110)*
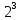
Умножаем мантиссы:
0.1001*0.1110 = 0.0111111 - > округляем по 6 разряд -> 0.011111
0.011111 *
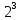= 11.111 переводим в 10ю -> 3.875Точное значение -> 11.1111 в 10ю -> 3.9375
Ответ : полученное значение при мантиссе 6 разрядов 3.875
Точное значение 3.9375.
Задача № 10:
Записать число а в ячейку памяти компьютера, предназначенную для типа REAL
a = –213,55
Переводим его в двоичное представление:
a= 11010101.10001100110 Находим порядок числа:
p=8
Переводим порядок в 2ю систему
=
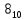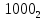
Находим машинный порядок по формуле
M= 1000000+p
M= 1001000
записываем число в 4-х байтовой ячейке
Первую ставим 1 т.к число отрицательное
|1100|1000|1101|0101|1000|1100|1100|0000|
Переводим каждую ячейку в 16ю систему:
C8D58CC0
Ответ : C8D58CC0