ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.












,
Задание 21. Что называется точкой разрыва функции? Как классифицируются точки разрыва? Какого рода разрывы имеют функции
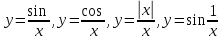 ?
?Задание 22. Сформулировать правило Лопиталя для раскрытия неопределенностей вида
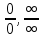 . Найти пределы используя правило Лопиталя:
. Найти пределы используя правило Лопиталя:








 Задание23. Сформулировать признак монотонности дифференцируемой функции на
Задание23. Сформулировать признак монотонности дифференцируемой функции на 

 3)
3) Задание 24. Сформулировать достаточные условия экстремума непрерывной функции. Найти точки экстремума функции:




 ,
,-


 , 6)
, 6) .
.
Задание 25. Какая кривая называется выпуклой вверх (вниз) на (а, в)? Что называется точкой перегиба кривой? Исследовать на выпуклость вниз (вверх) и найти точки перегиба графиков следующих функций:
-


 , 2)
, 2)
Задание 26. Что называется асимптотой кривой? Какие асимптоты может иметь кривая? Найти асимптоты заданных кривых:
-




 , 2)
, 2) , 3)
, 3) , 4)
, 4)  ,
,
-



 , 6)
, 6) , 7)
, 7) .
.

Задание 27. На основании основных правил нахождения производных, найдите производную функции у(х) = 5х2 – 3х + 4.
Задание 28. Дайте определение производной функции в точке.
Найдите производную функции у(х) = х5-5х3+12х2- 140.
Задание 29. Вычислить а)
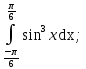 б)
б) 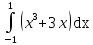 .
.Задание 30. Вычислить:
а) с точностью до 0,0001 определенный интеграл
 ;
;б) с точностью до 0,0001 определенный интеграл
 .
.Задание 31. Найти область определения функции:
а)
Задание 32. Найти пределы:


Задание 33. Найти пределы, используя первый замечательный предел:








 Задание 34. Найти пределы, используя второй замечательный предел:
Задание 34. Найти пределы, используя второй замечательный предел: 


 Задание 35. Найти производных следующих функций1)
Задание 35. Найти производных следующих функций1) 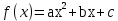 ; 2)
; 2) 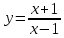 ; 4)
; 4) 
 Задание 36. Найдите мгновенную скорость движения тела в момент
Задание 36. Найдите мгновенную скорость движения тела в момент Задание 37 . Исследовать на экстремум следующие функции:
 1)
1) 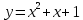 ; 2)
; 2) 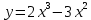 . 3)
. 3) 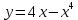 .
.Задание 38. Найти точки перегиба функции и интервалы выпуклости (вогнутости) графиков следующих функций:
