t_зх = t_з K_lK_hK_K3K_h1/lK_HK_пK_tk (15)

3.1.2 Расчет теплового режима блока

Требуется рассчитать температуру t_з нагретой зоны аппарата с внешними размерами L₁ = 0.66 м, L₂ = 0.28 м и h = 0.15 м. Шасси расположено горизонтально в средней части аппарата и занимает все его сечение. Детали расположены сверху и снизу шасси равномерно, коэффициент заполнения k_з равен 0.25. Все поверхности имеют степень черноты 0.9. Давление снаружи аппарата 0.08 МПа, температура окружающей среды равна 20 °С. Мощность рассеиваемой аппаратом тепловой энергии 120 Вт.

1) Проведем вспомогательные расчеты:

S_k = 2(hL₂ + L₁h + L₂L₁) = 2*(0.15*0.28+0.66*0.15+0.28*0.66) = 0.651 м²;

P_уд.к = P/ S_k = 80 / 0.651 = 122 Вт/м²;

l = L₁ L₂ =  0.66*0.28 = 0.4 м;

h₃ = k₃h = 0.25*0.15 = 0.03 м;

h₁ = 0.5( h –h₃ )= 0.5*(0.15 – 0.03) = 0.06 м;

h₁ / l = 0.06 / 0.4 = 0.15

S₃=2(h₃L₂ + L₁h₃ + L₂L₁)=2*(0.03 *0.28+0.66*0.03+0.28*0.66) = 0.426 м²;

P_уд.3 = P/ S₃ =80 / 0.426 = 187,79 Вт/м²;

2) Рассчитаем температуру кожуха при P_уд.к =122 Вт/м²; t_c = 46° С;  =0.9; S_k = 0.651 м²; H = 753 мм рт. ст.

По графикам рисунок 5–4 /3/ стр. 164 определяем значения V_Pk и коэффициентов k_x:

V_Pk = 17 град; k_t = 1; k_ = 1; k_S = 1; k_H = 1

По формуле (13) находим температуру V_k перегрева кожуха над средой

V_k = 17*1*1*1*1 = 17 град

Температура кожуха t_k = t_c + V_k = 46 + 17 = 63 °С

3) Рассчитаем температуру зоны при P_уд.з = 187,79 Вт/м²; l = 0.4 м; k₃ = 0.25; h = 0.15 м; h₁/ l = 0.15; _п = 0,81; t_k = 63 °С; H =753 мм рт. ст.

По графикам 5–6 /3/ стр. 167 определяем значения t_з и коэффициентов K_x:

t_з = 17 град; k_k3 = 1; k_h = 1.01; k_h1/l = 1.05; k_l = 1.04; k_п= 0.98; k_tk = 1.02; k_H = 1.

По формуле (15) находим разность t_з температур между нагретой зоной и кожухом:

t_з.к = 17*1*1.01*1.05*1.04*0.98*1.02*1 = 17.2 град

Температура нагретой зоны:

t_з = t_к + t_з.к = 63 + 17.2 = 80.2 °С

3.2 Выбор конструкции и расчет параметров радиатора для элемента с наиболее тяжелым тепловым режимом

3.2.1 Эффективный коэффициент теплоотдачи радиатора

Для системы воздушного охлаждения широкое применение получили радиаторы, которые различаются по виду развитой площади поверхности, а именно: пластинчатые, ребристые, игольчато-штыревые, типа «краб», жалюзийные, петельно-проволочные.

---

Исследования теплообмена радиаторов различного типа позволили построить приближенную зависимость среднего перегрева V_s = t_s-t_c основания площадью A от удельной нагрузки q = Ф/ A (A=L₁L₂, A=D²/4) при свободной и вынужденной вентиляции. Этот график приведен в приложении Б.5 /1/ и позволяет остановиться на том или ином типе радиатора, если заданы поверхностная плотность теплового потока q и допустимый перегрев V_s основания.

Для характеристики теплообменных свойств радиатора используют следующие параметры: эффективный коэффициент теплоотдачи _эф, тепловую проводимость _, тепловое сопротивление R_. Эти параметры связаны со средним перегревом V_s основания и рассеиваемым потоком Ф зависимостями:

_эфA=_ =R^-1_ , A=L₁L₂ , A = D²/4 , Ф = __s = R^-1__s = _эф _s A (16)

где L₁, L₂ – размеры основания прямоугольного радиатора;

D – диаметр круглого основания.

Формула (16) справедлива для радиатора любого из рассмотренных выше типов; вся сложность процессов переноса теплоты и конструктивные особенности сосредоточены здесь в одной величине – эффективном коэффициенте теплоотдачи. Последний может быть определен экспериментально или расчетным путем. В первом случае в основу положена зависимость (16), позволяющая по найденным из опыта значениям Ф и V_s определить _эф . В приложении Б.5 /1/ приведены полученные таким способом зависимости для различных типов выпускаемых промышленностью радиаторов. С помощью этих графиков можно подобрать радиатор, средняя температура основания которого не превышает заданной величины.

Рассмотрим теперь на примере пластинчатых, ребристых и игольчато-штыревых конструкций радиаторов расчетный метод определения параметров _эф, _ или R_. Необходимость анализа процесса теплообмена радиаторов связана с непрерывным изменением выпускаемых промышленностью типоразмеров радиаторов. Представим тепловую модель одиночного ребра или штыря в виде стержня произвольного сечения f с периметром U и длиной h, находящегося в среде с температурой t_c и коэффициентом теплоотдачи с боковой поверхности . Перегрев х_i торца стержня i, в который входит поток Фi определяется по формуле:

---

_i = [ Ф_i/ (fb)]ctgbh` , b<sup>2</sup> = U/(f) , h` = h + f/U. (17)

Тепловое сопротивление R_i одиночного стержня на основании этой зависимости и формулы (16):

R_i = _I^-1 = v_i / Ф_i = ctgbh`/ (fb). (18)

Общая проводимость _р оребренной части радиатора равна сумме проводимостей _i всех N ребер:

_р = = N_i. (19)

Если проводимость от неоребренной части радиатора равна _Hр , то общая проводимость радиатора:

_ = _нр + Nfb_thb_h`. (20)

Параметр b содержит коэффициент теплоотдачи боковой поверхности ребра или штыря, который определяется из соответствующих критериальных уравнений. В частности, для вынужденной конвекции воздушной среды может быть рекомендована формула:

N_u = L/_в = 0,21 Re^0,8 , Nu = L/_в , Re = _pL/v_в (21)

где _в , _в – теплопроводность и кинематическая вязкость воздуха при средних значениях температур;

L – определяющий размер для данного вида оребрения;

_p– расчетная скорость движения воздуха для данного вида оребрения.

Особенности теплообмена радиатора учтены выборе параметров L и _p, которые равны для ребристых поверхностей _p = 1,25, L = L₁ , для игольчато-штыревых радиаторов L = d, _p = S_ш/( S_ш - d), где – средняя скорость движения воздуха; S_ш – шаг оребрения; d – диа­метр штыря.


3.2.2 Методика выбора и расчета радиатора

На рисунке 1 схематически изображен радиатор 1 с закрепленным на нем прибором 2, внутри которого имеются источники мощностью Ф, разогревающие рабочую область прибора и его корпус до температур t_р и t_к; в месте крепления прибора к радиатору температура основания радиатора t_и , а средняя температура основания радиатора t_s.

Приведем исходную информацию, которая должна быть при проектировании или выборе радиатора: предельно допустимая температура рабочей области прибора (t_р)_доп или его корпуса (t_к)_доп; рассеваемая прибором мощность Ф; температура t_с окружающей среды или набегающего потока; внутреннее тепловое сопротивление R_вн прибора между рабочей областью и корпусом; способ крепления прибора к радиатору, который характеризуется тепловым сопротивлением R_к контакта. Проектируемый радиатор должен удовлетворять некоторым дополнительным требованиям: иметь малую массу и габариты, выполнять свои функции при наименьшем расходе воздуха, если требуется принудительное охлаждение.

---

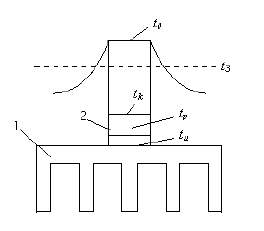
Рисунок 1 – Температурное поле радиатора и прибора
На рисунке 1 представлена схема соединения тепловых сопротивлений между рабочей областью и окружающей средой, из которой следует:

t_p – t_c = (t_p - t_k)+(t_k -t_и)+(t_и-t_c); (22)

t_и-t_c = (t_p – t_c) – Ф(R_вн + R_k).

Введем безразмерную величину в, связывающую среднюю температуру t_s основания радиатора и температуру t_и в месте крепления прибора к радиатору:

 = (t_и - t_c)/(t_s - t_c) = f(B, ); (23)

она зависит, как показано в приложении Б.2 /1/, от двух чисел подобия:

B = (₁ + ₂)A_p / () и (24)

где: ₁ и ₂ – коэффициенты теплоотдачи с одной и другой сторон радиатора;

A_р , A_и – площади оснований радиатора и прибора;

 - толщина основания радиатора;

 - теплопроводность материала радиатора.

Функциональная зависимость (23) может быть найдена для любого положения источника на радиаторе и любых значений его размеров. Из формул (22) и (23) получаем:

t_s – t_c = [(t_p - t_c) – Ф(R_вн –R_K)]/. (25)

Все параметры, входящие в квадратные скобки формулы (25), заданы, а параметры (t_s – t_с) и  неизвестны. Дальнейший подбор радиатора может быть осуществлен с помощью формул (16), (25) и графиков, представленных на рисунках Б.8 – Б.12 /1/ на основе метода последовательных приближений. В первом приближении задают значение ¹ = 1,2 и по формуле (25) определяют (t_s – t_c), затем в первом приближении задают площадь A_р основания радиатора и по графикам рисунок Б.12 /1/ подбирают вид оребрения и характер теплообмена (свободная или вынужденная конвекция). Зная Ф, A_р и (t_s – t_c), по формуле (16) находят в первом приближении эффективный коэффициент теплоотдачи _эф.

По графикам, представленным на рисунке Б.8 – Б.11 /1/, уточняют геометрические размеры параметры радиатора, после чего переходят ко второму приближению расчетов, а именно: находят безразмерные числа B = _эф A_p / () и по графику рисунок Б.3 /1/ опре­деляют ^II и уточняют по формуле (23) значение (t_s

---

– t_с).
3.2.3 Выбор конструкции и расчет параметров радиатора

Требуется подобрать радиатор для охлаждения транзистора KT805, рассеивающего мощность Ф = 15 Вт и находящегося внутри блока. Контакт транзистора с радиатором осуществлен по площади A_и = 0.00024 м²; внутреннее тепловое сопротивление прибора R_вн = 1.2 °К/Вт, тепловое сопротивление контакта R_к = 2 °К/Вт, допустимая температура кол­ле­к­торного перехода в транзисторе t_рдоп = 150 °С; допустимая температура корпуса в транзисторе t_кдоп = 125 °С; условия теплообмена – свободная конвекция, температура воздуха в блоке t_с = 46 °С.

1) По формуле (25) определяем температуру t_и в месте крепления транзистора:

(t_и - t_c) = (125 – 46) – 15*(1,2 + 2) = 31 °С.

2) В первом приближении принимаем ^I = 1.2 и из (23) находим

(t_s - t_c)¹ = 31/1.2 = 25.8 °С.

3) Задаем для простоты в первом приближении площадь A_р основа­ния; пусть A_р = 0.66*0.28 = 0.1848 м². Тогда плотность теплового потока:

q = 15 / 0.1848 = 81 Вт/м².

4) По графику, приведенному на рисунке Б.12 /1/ для (t_s – t_с)¹ = 31 °С и q = 329 Вт/м², определяем возможный вид оребрения радиатора в условиях свободной конвекции; как следует из графиков, необходимо выбрать пластинчатый радиатор.

5) По формуле (16) определяем коэффициент эффективной теплоотдачи, необходимый для обеспечения заданного теплового режима. По графикам, представленным на рисунке Б.8 /1/, наиболее близкий профиль оребрения штыревого радиатора соответствует h₁ = 20 мм, S_ш = 7 мм, d = 2 мм, для которого _эф = 65 Вт/( м²·К).

6) Находим по формулам (24) второе приближение ^II, полагая _эф, а также выбирая материал радиатора, например дюралюминий  = 180 Вт/(м·К):

B = 65*0.1848/ (180*2,5*10^-3) = 5.4;

A_и / A_р = 0.001848 / 0.1848 = 0.01.

По графику рисунок Б.3 /1/ находим ^II = 1.7 и уточняем по формуле (23) перегрев:

(t_s – t_с)^II =31/ 1.7 = 18.2 °С.

7) Уточняем размеры основания и тип радиатора. Согласно графику, приведенному на рисунке Б.12 /1/, для (t_s – t_с)¹ = 31 °С и q = 329 Вт/м² тип радиатора остается прежним. Таким образом, окончательно останавливаемся на радиаторе штыревого типа из дюралюминия с площадью основания A =0.1848 м² (L₁ = 660 L₂ = 280 мм), h = 20 мм, S_ш = 7 мм, d = 2 мм, эскиз которого приведен на рисунке 2.

---

Смотрите также файлы

• Государственное образовательное учреждение высшего профессионального образования донецкий национальн.doc

• Стили управления.docx

• Спросом в экономике является желание и способность потребителя, приобрести товар или услугу. К примеру, в России, всегда будет спрос на покупку жилья, связано с различными выгодными предложениями ипотека от банка, ипотека от застройщика под минимальный п.docx

• Учебное пособие по выполнению выпускных квалификационных работ для студентов Инженерноэкономического института.docx

• Уроках математики Цель обучения ребенка состоит в том, чтобы сделать его способным развиваться дальше, без помощи учителя.docx