Методические указания
Расчет ведется в предположении, что отказы каждой из двух подсистем независимы,
т.е. отказ первой подсистемы не нарушает работоспособность второй, и наоборот.
Вероятности безотказной работы каждой подсистемы одинаковы и равны Р_П (T _П ).



Тогда вероятность отказа одной подсистемы:


QП (T П ) 1− P_П (T П )



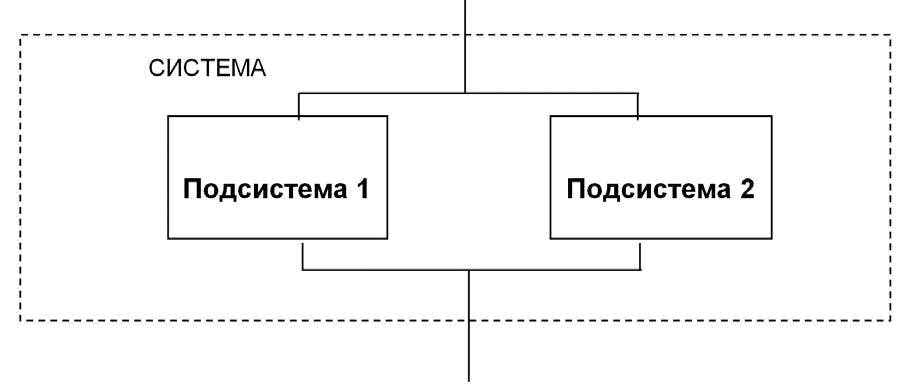
Вероятность отказа всей системы Q_С (T П ) определяется из условия, что отказала и первая, и вторая подсистемы, т.е.:

---

Параметр						Предпоследняя цифра шифра
		0	1		2	3	4	5	6	7	8		9
							Первое	измерение
t1		50		25	75	80	40	60	90	30	65		20
y	1	1,49		0,81	2,18	2,32	1,22	1,77	2,59	0,94	1,91		0,67
D(y1)		0,098		0,05	0,147	0,157	0,079	0,118	0,176	0,06	0,128		0,04
						Второе измерение
t2		150		125	175	180	140	160	190	130	165		120
y	2	4,24		3,56	4,93	5,07	3,97	4,52	5,34	3,69	4,66		3,42
D(y2)		0,292		0,244	0,341	0,351	0,273	0,312	0,37	0,254	0,322		0,234
							11

---

y(t)

---

Методические указания
Данное задание выполняется в предположении, что математическое ожидание (среднее значение) и дисперсия проката бандажей представляют собой линейные функ-ции пробега локомотива. Это подтверждается исследованиями, проведенными в депо.
Обозначим прокат бандажей как некоторую переменную величину Y. Зависимость Y от наработки (пробега локомотива) представляет собой случайную функцию, реализации которой являются монотонными неубывающими функциями. Для описания такой слу-чайной функции часто вполне достаточно знать, как изменяются в зависимости от нара-




ботки ее математическое ожидание (среднее значение) и дисперсия: и D(у).

Исследования, проведенные в различных депо, показывают, что для описания зависимости проката бандажа колесной пары от пробега локомотива могут быть использованы линейные функции. В соответствии с этим запишем:

		(t)		0at ,
	y		y		(14)
D(y(t)) D(y0)bt ,					(15)

D(y)=0.002+0,00194*7.5=0.016; y(t)=0.115+0.027*7.5=0.317

где y₀ и D(y₀) соответственно – среднее значение и дисперсия проката бандажей при t = 0, при этом началом отсчета является последняя обточка бандажей;

• 
  – средняя скорость увеличения проката, мм/тыс. км;
  

2. 
   – скорость увеличения дисперсии проката,мм²/тыс.км;t – пробег локомотива, тыс.км.
   

Искомыми параметрами функций (14) и (15) являются y₀ , a , D(y₀) и b. На практи-ке для их нахождения необходимо область возможных значений наработки (нижняя гра-ница которой t = 0, а верхняя находится из условия достижения предельного значения проката) разбить на несколько (обычно 10–20) интервалов. При каждом из разделяемых этими интервалами пробегов локомотива t

---

₁, t₂,….., t_j,… производят измерения проката




большого количества колесных пар и вычисляют соответствующие пробегам средние значения y₁ , y₂ ,….., y _j ,…., а затем дисперсии D(y₁), D(y₂), ... , D(y_j), … . Располагая




такими наборами значений, можно, используя метод наименьших квадратов, определить искомые зависимости y(t) и D(y).

• 
  контрольной работе задача существенно упрощена. Предполагается, что массивы данных о прокате бандажей для каждого t_j уже обработаны. Считается также возможным определить искомые линейные зависимости, располагая координатами только двух точек.
  

• 
  таком случае параметры а и b зависимостей (14) и (15) могут быть определены:
  

a=		y 2		− y1	,	a= 2.75/100=0.027	(16)
				-t1
		t	2
b	D(y2)− D(y1)					.	(17)
			t2−t1

---

Смотрите также файлы

• Практическое задание Заполнить таблицу Методы поиска новых решений.docx

• Содержание Введение История возникновения волейбола Содержание и правила игры Специфика волейбола Техника игры Тактика игры Введение.docx

• Вторник1 8 00 00.pdf

• Конспект викторины по изо весёлые художники.doc

• Квест по информационной безопасности.docx