ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 12
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Матрицы, действия над матрицами
Ответ:
Сложение матриц;Умножение матрицы на число;Умножение матриц друг на друга (применимо, если матрицы согласованы друг с другом — то есть, матрица $A$ должна иметь количество столбцов, равное количеству строк в матрице $B$);Транспонирование матрицы; *Умножение матрицы на вектор-столбец или строку;Вычисление определителя матрицы.
2. Определители 1-го, 2-го, 3-го порядков. Правило
треугольников.
Ответ:



Метод приведения к треугольному виду.Используя свойства, добьемся такой структуры определителя, при которой все его элементы, стоящие ниже главной диагонали, равны нулю. Тогда определитель будет численно равен произведению элементов, стоящих на главной диагонали.
3 Определители n-го порядка. Теорема Лапласа.
Ответ:


4 Обратная матрица. Алгоритм нахождения обратной
матрицы.
Ответ:



5 Ранг матрицы. Алгоритм вычисления ранга матрицы с
помощью элементарных преобразований.
Ответ:

Под элементарными преобразованиями строк (столбцов) матрицы понимают следующие действия:Перемена мест двух строк (столбцов).Умножение всех элементов строки (столбца) на некоторое числоa≠0.Суммирование всех элементов одной строки (столбца) с соответствующими элементами иной строки (столбца), умноженными на некое действительное число.Если применить к строкам или столбцам матрицыAнекое элементарное преобразование, то получим новую матрицуB. В этом случаеrang A=rangB, т.е. элементарные преобразования не изменяют ранг матрицы.ЕслиrangA=rangB, то матрицыAиBназываются эквивалентными. Тот факт, что матрицаAэквивалентна матрицеB, записывают так:A∼B.Часто используется и такая запись:A→B, которая означает, что матрицаBполучена из матрицыAприменением некоего элементарного преобразования.При нахождении ранга методом Гаусса работать можно как со строками, так и со столбцами. Удобнее работать со строками, поэтому в примерах на этой странице преобразования выполняются именно над строками матриц.Отмечу, что транспонирование не изменяет ранг матрицы, т.е.rang A=rangA^T. Этим свойством в некоторых случаях удобно пользоваться так как при необходимости строки легко сделать столбцами и наоборот.
6 Система линейных уравнений. Метод обратной матрицы.
Формулы Крамера. Метод Гаусса.
Ответ:





7 Векторы и операции над ними.
Ответ:



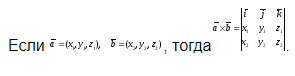

8.Проекция вектора на ось и ее свойства.
Ответ:


9. Декартова прямоугольная система координат. Полярная
система координат.
Ответ:


10 Скалярное, векторное и смешанное произведения векторов.
Ответ:





11 Предел функции в точке. Основные теоремы о пределах.
Ответ:


12 Предел функции при x, стремящемся к бесконечности.
Замечательные пределы. Число е.
Ответ:


e — математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. e = 2,718281828459045… Иногда число e называют числом Эйлера или неперовым числом. Играет важную роль в дифференциальном и интегральном исчислении.
13 Непрерывность функции в точке и на промежутке. Точка
непрерывности функции. Точка разрыва функции. Свойства
непрерывных функций. Приращение аргумента. Приращение
функции.
Ответ:
Функциюy = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.
Функция называется непрерывной в точке если существует предел функции в этой точке и он равен значению функции в точке. Использование последней формулы существенно упрощает вычисление пределов для непрерывных функций. Функция называется непрерывной на промежутке, если она непрерывна в каждой его точке. График такой функции — непрерывная кривая
Точкой разрыва функции называют значение ее аргумента, при котором функция не является непрерывной или при котором функция не определена. Если - точка разрыва и существуют конечные пределы то она называется точкой разрыва первого рода. Величину называют скачком функции в точке. Если - точка разрыва и, то называют точкой устранимого разрыва.

разность между двумя значениями аргумента, то есть хПриращение аргумента — это разность между двумя значениями аргумента, то есть х.Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению.Отсюда мы получаем определение производной функции.Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции.
разность между двумя значениями функцииПриращение функции — это разность между двумя значениями функции, то есть у.Приращение аргумента — это разность между двумя значениями аргумента, то есть х.Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению.Отсюда мы получаем определение производной функции.
14 Производная функции. Дифференциал функции.
Геометрический смысл производной. Механический смысл
производной.




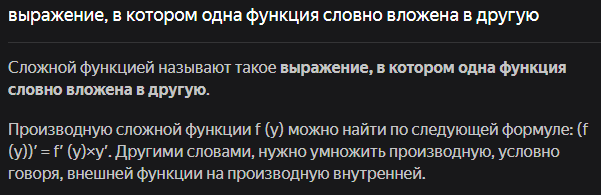
15 Таблица производных. Понятие сложной функции.
Производная сложной функции.
Ответ:


16 Схема исследования функции. Область определения
функции. Множество значений функции. Четность и
нечетно сть функции. Нули функции. Промежутки
знакопостоянства функции. Возрастание и убывание функции,
правило нахождения промежутков монотонности. Точки
экстремума функции, правило нахождения экстремумов
функции.





Возрастание и убывание функции. Кроме непосредственно значений функции важно понимать, как изменяется ее значение с изменением аргумента, т. е. уметь анализировать поведение функции. Так, говорят, что функция возрастает
, если при увеличении аргумента значение функции увеличивается. Соответственно, функция убывает, если при увеличении аргумента значение функции уменьшается.
Промежутки возрастания и убывания функций называются промежутками монотонности функций.Для их определения находят производную функции, приравнивают ее к нулю и находят корни производной. Этими корнями разбивают область определения функции на промежутки. В каждом из промежутков берут внутри точку и устанавливают знак производной в них. В тех промежутках, где производные положительные, функция возрастает, а где отрицательные — убывает.
Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).Итак, чтобы определить точки экстремума функции, требуется выполнить следующее: Найти производную функции. Приравнять производную нулю и определить критические точки. Мысленно или на бумаге отметить критические точки на числовой оси и определить знаки производной функции в полученных интервалах. Если знак производной меняется с "плюса" на "минус", то критическая точка является точкой максимума, а если с "минуса" на "плюс", то точкой минимума.
17 Производные высших порядков. Физический смысл второй
производной. Исследование функции с помощью второй
производной.

Физический смысл производной заключается в том, что мгновенная скорость изменения любой физической величины равна производной этой величины по времени. Так, в механике, наиболее распространенными физическими величинами являются координаты точки. При прямолинейном движении, мгновенная скорость движения точки равна производной ее координаты по времени.

18 Первообразная. Неопределенный интеграл. Основные
свойства неопределенного интеграла.


19 Таблица неопределенных интегралов.


