Контрольная работа №1

Вариант 12

E1, B	E2, B	E3, B	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
120	160	250	210	200	100	120	180	170

1.1. Преобразование цепи



Узлы c и d являются общими для резисторов R₂, R₃, R₄. Следовательно, эти резисторы соединены параллельно. Общая проводимость соединенных параллельно ветвей равна сумме проводимостей отдельных ветвей.









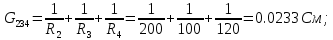
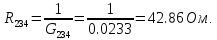
Эквивалентное сопротивление цепи равно сумме соединенных последовательно резисторов R₁, R₂₃₄.





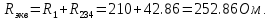
1.2. Расчет неизвестных токов по законам Кирхгофа

Выберем произвольно направление токов ветвей и обозначим узлы схемы. Направление обхода контуров против часовой стрелки.



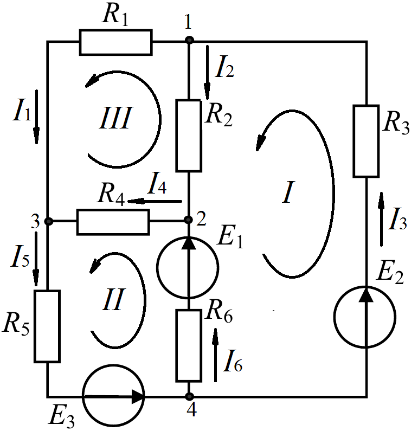
Число уравнений, составленных по первому закону Кирхгофа, равно k = n – 1, где n – число узлов схемы.

k = 4 – 1 = 3







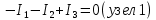
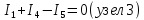
Число уравнений, составленных по второму закону Кирхгофа

---

, равно m = i – k = 6 – 3 = 3, где i – число неизвестных токов. Общее число уравнений 6.







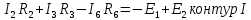
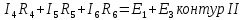
Система уравнений по методу контурных токов:



После подстановки численных значений получим систему уравнений:



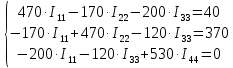
Решим систему уравнений методом Крамера.

Определители системы уравнений равны:









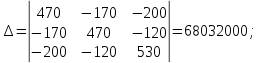
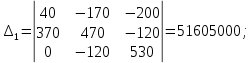
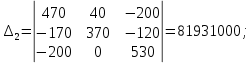
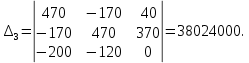
Решение системы уравнений:





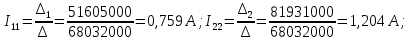
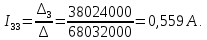
Токи ветвей:





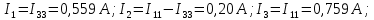
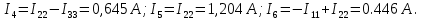
Составим баланс мощности









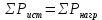
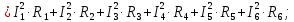
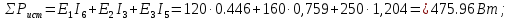
Источники ЭДС работают в режиме генератора энергии, т. к. направления ЭДС и тока через источники совпадают.



Баланс выполняется, задача решена верно.

Относительная погрешность расчета:



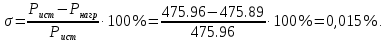
Потенциальная диаграмма

Потенциалы точек:

---

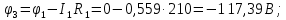
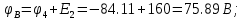
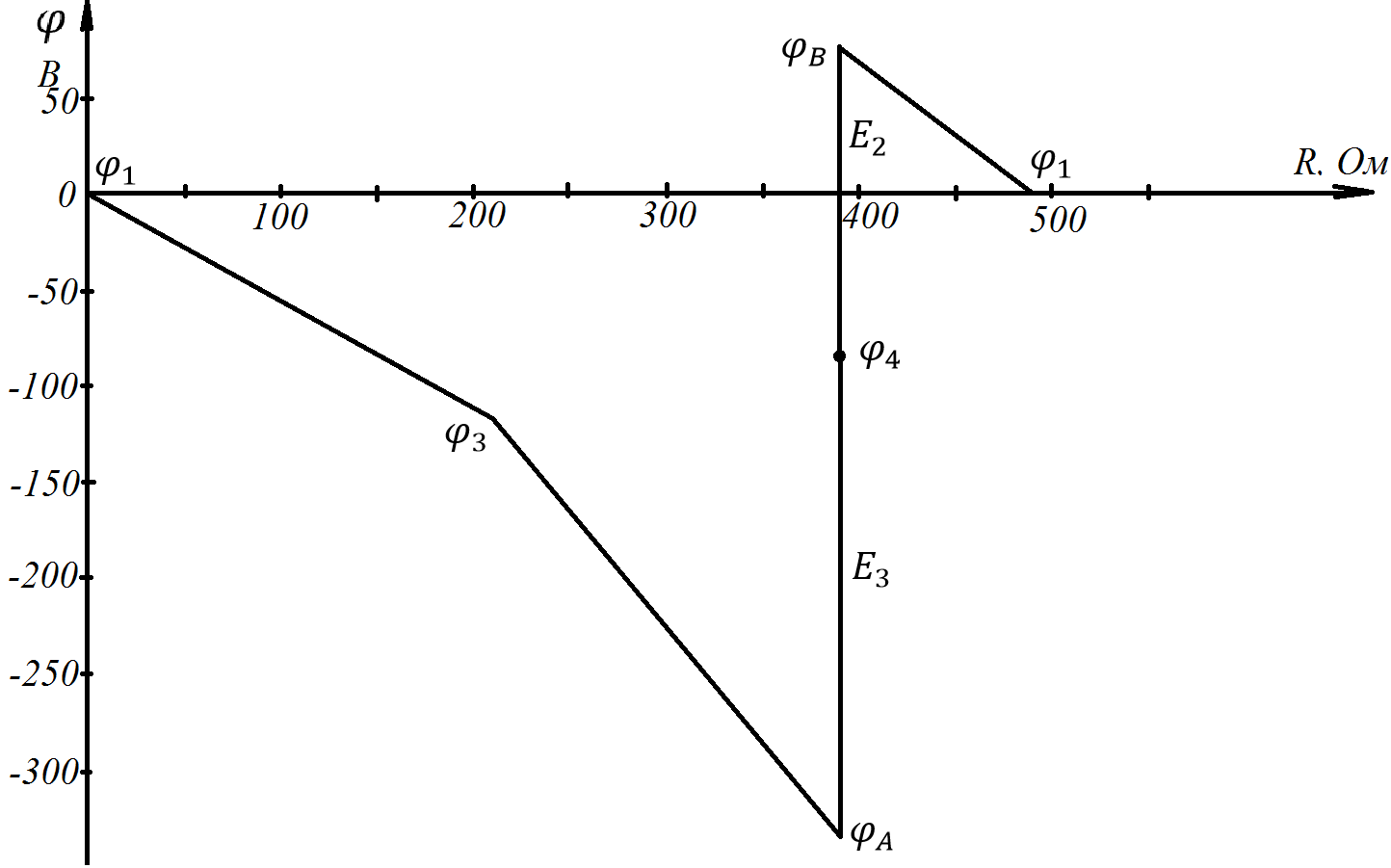
Выводы:

В пункте 1.1 работы мы изучили различные способы соединения нагрузки – последовательное, параллельное, смешанное и методы расчета эквивалентного сопротивления цепей.

В пункте 1.2 работы мы изучили метод расчета сложной цепи постоянного тока составлением системы уравнений по законам Кирхгофа. Рассчитали заданную цепь методом контурных уравнений, требующим для решения меньшего числа уравнений. Для решения системы из трех уравнений (по количеству независимых контуров) применили метод Крамера. Правильность решения задачи проверили составлением уравнения баланса мощностей и построили потенциальную диаграмму внешнего контура.

Литература:

1. 
   Мартынова И.О. Электротехника: учебник для СПО. М.: КноРус, 2017. 304 с.
   
2. 
   Фуфаева Л.И. Электротехника: учебник для СПО. 5-е изд. М.: Академия, 2016. 384 с.
   

---

Смотрите также файлы

• Закон спроса. Спрос и его величина. Эластичность спроса Закон предложения. Предложение и величина предложения. Эластичность предложения Рыночное равновесие. Излишки потребителя и производителя.docx

• Основные политические центры Руси. Этапы объединения русских земель в единое государство. Причины возвышения Москвы.docx

• Закон спроса. Спрос и его величина. Эластичность спроса Закон предложения. Предложение и величина предложения. Эластичность предложения Рыночное равновесие. Излишки потребителя и производителя.docx

• Растения. Ботаника.docx

• Аддитивное смешение цветов.docx