Файл: Лабораторная работа 1 По дисциплине Моделирование процессов и систем СанктПетербург 2022.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.04.2024
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Лабораторная работа №1
По дисциплине Моделирование процессов и систем
\
Санкт-Петербург
2022
Постановка задачи(цель)
Рассмотрим одноканальную замкнутую систему массового обслуживания (СМО) с неограниченным временем ожидания требований для него и с простейшим потоком. Этот поток наиболее полно отвечает реалиям жизни и характеризуется следующими особенностями:
-
поступление требований в систему на обслуживание происходит по одному, то есть вероятность прибытия двух и более требований одновременно очень мала, и поэтому ею можно пренебречь (поток требований ординарный); -
вероятность поступления последующих требований в любое время не зависит от возможности их прибытия ранее – поток требований без последействия; -
поток требований стационарный.
Выявление основных особенностей, взаимосвязей и количественных закономерностей
Функционирование любой системы массового обслуживания можно представить через все возможные ее состояния и интенсивность перехода из одного состояния в другое. Основными параметрами функционирования системы массового обслуживания являются вероятности ее состояния, то есть возможности наличия n требований (покупателей, рабочих, заданий, машин, неполадок) в системе – Pn. Так, вероятность P0 характеризует состояние, когда в системе нет требований и канал обслуживания простаивает.
Важным параметром функционирования системы массового обслуживания является также среднее требований, находящихся в системе N
сист, то есть в очереди на обслуживание, и средняя длина очереди Nоч. Исходными параметрами, характеризующими СМО, являются: число каналов обслуживания N (касс, компьютеров, кранов, ремонтных бригад); число требований m (покупателей, рабочих, заданий, машин, неполадок), интенсивность поступления одного требования на обслуживание λ, то есть число поступлений требований в единицу времени; интенсивность обслуживания требований μ.
Интенсивность поступления требований на обслуживание определяется как величина, обратная времени возвращения требования tвоз:
λ=1/tвоз
Интенсивность обслуживания требований определяется как величина, обратная времени обслуживания одного требования – tобс:
μ=1/tобс
Решение задачи с использованием системы Mathcad
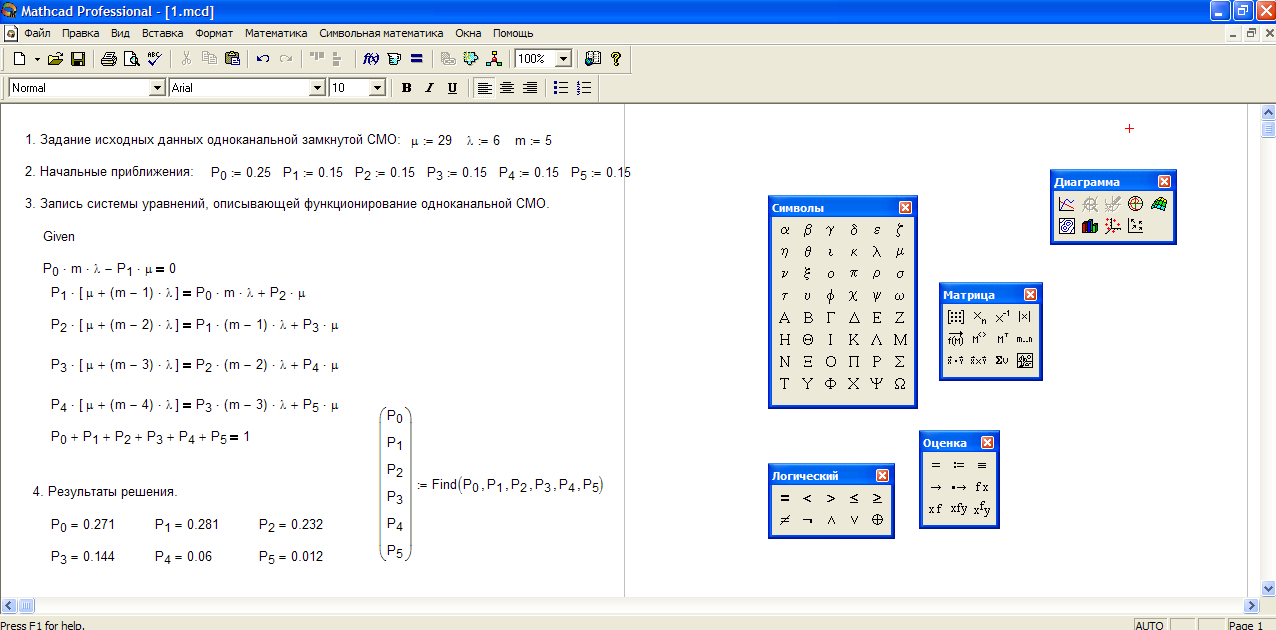
Введены исходные данные, начальные приближения, система уравнений, описывающая функционирование одноканальной СМО. Получены результаты решения.
Рассмотрим неустановившийся режим работы системы массового обслуживания, когда ее основные вероятностные характеристики зависят от времени, например в течение 0,3 часа.
В этом случае интенсивности входных и выходных потоков для каждого состояния будут сбалансированы, но уже с учетом производных вероятностей.
Таким образом, мы будем иметь систему обыкновенных дифференциальных уравнений, описывающих функционирование одноканальной замкнутой системы при неустановившемся режиме.
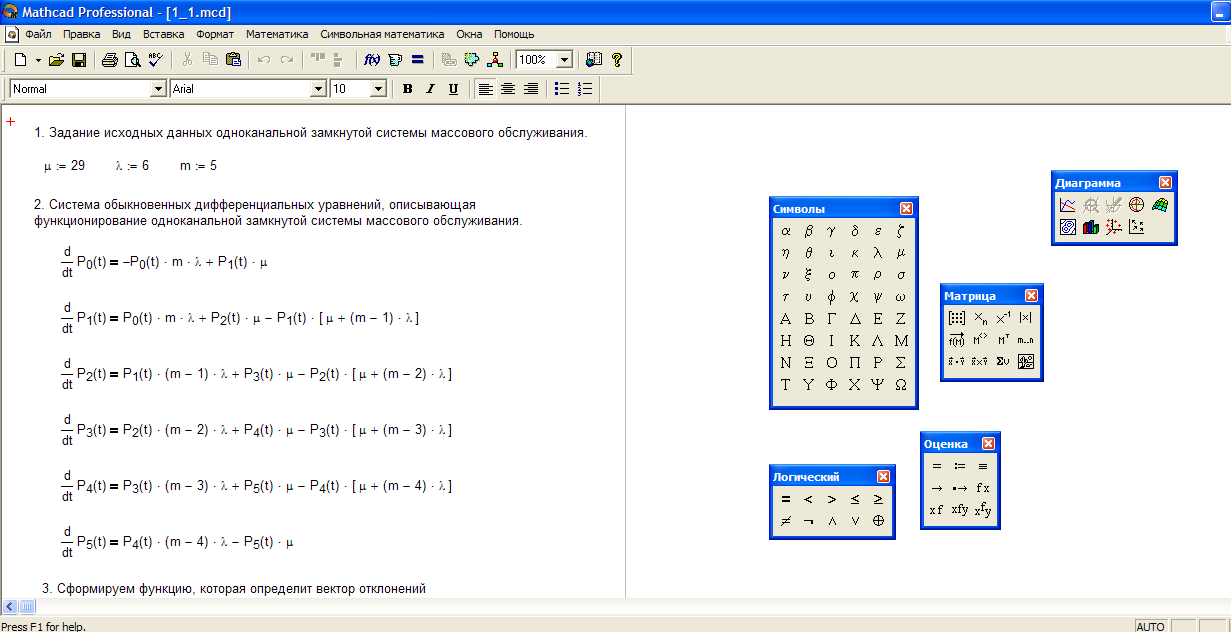
Начальные исходные данные и система дифференциальных уравнений, описывающих функционирование одноканальной замкнутой СМО при неустановившемся режиме работы.
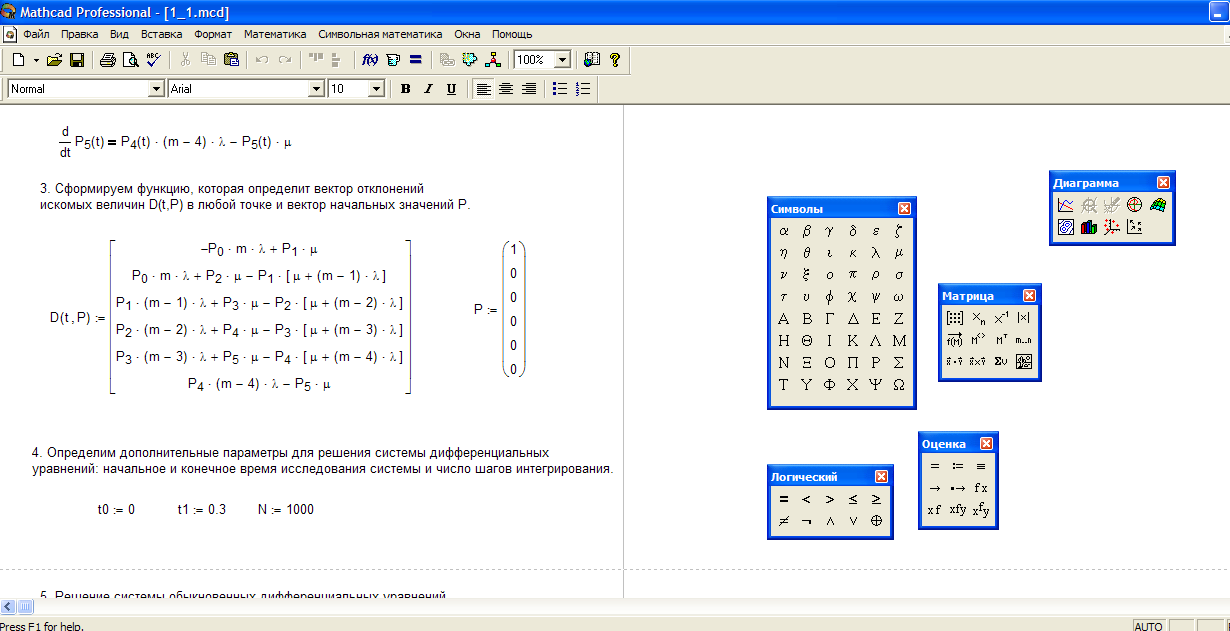
Функция, определяющая вектор отклонений искомых величин D(t,P) в любой точке и вектор начальных значений P; начальное и конечное время исследования системы и число шагов интегрирования
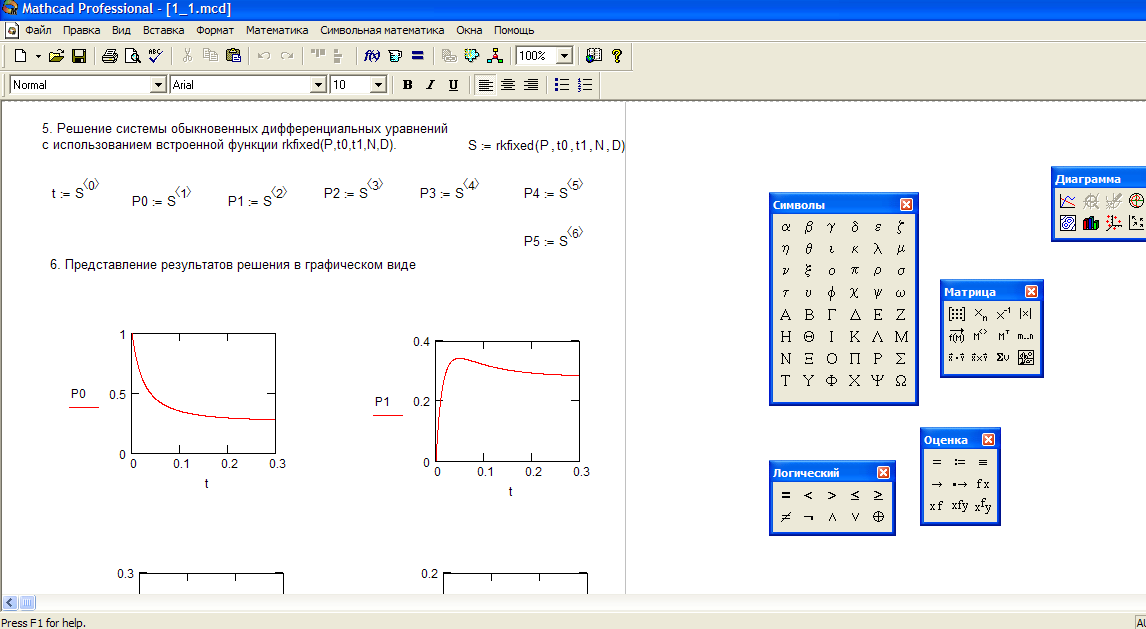
Решение системы дифференциальных уравнений с использованием встроенной функции rkfixed(P,t0,t1,N,D); представление результатов решения в графическом виде
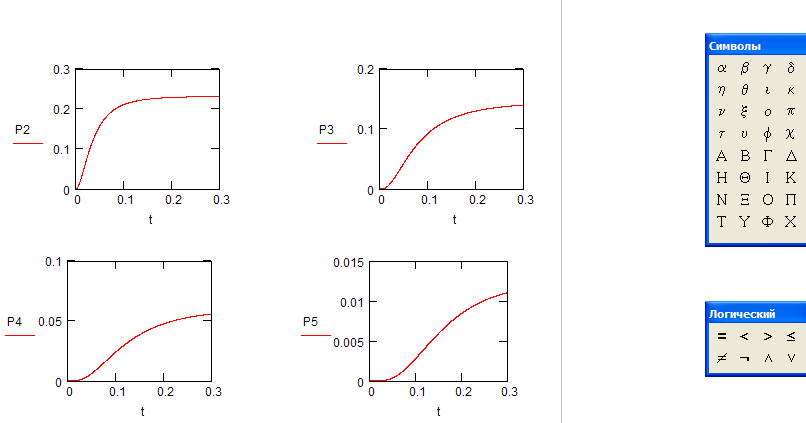
Вывод: В ходе лабораторной работы я рассмотрел одноканальную замкнутую систему массового обслуживания (СМО) с неограниченным временем ожидания требований для него и с простейшим потоком.
