Решение

1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 2, 3, 4, 5, соединенных нитями. Изобразим действующие на систему внешние силы: активные , , , , , , реакции , , , , , силы трения , , и моменты и (рис.2).

Для решения задачи можно определить скорость любого тела механической системы и далее, используя кинематические связи тел механизма, найти требуемы скорости.

Определим вначале скорость груза 2 .

Для определения скорости воспользуемся теоремой об изменении кинетической энергии:

. (1)

2. Определяем и . Так как в начальный момент времени система находилась в покое, то

---

. Величина равна сумме кинетических энергий всех тел системы:

. (2)

Учитывая, что тела 1 и 2 движутся поступательно, тела 4 и 5 вращается вокруг неподвижной оси, а тело 3 совершает плоскопараллельное движение, получим

;

;



;

. (3)

Все входящие сюда скорости необходимо выразить через искомую . Для этого предварительно заметим, что точка – мгновенный центр скоростей катка 3, радиус которого обозначим . Из рис.2 имеем:

;

;

;

;

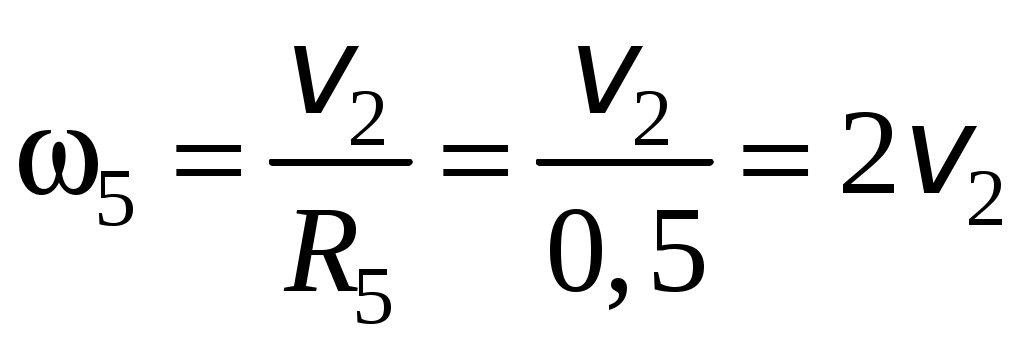. (4)

Кроме того, входящие в (3) моменты инерции имеют значения:

; ; . (5)

Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно

---

. (6)



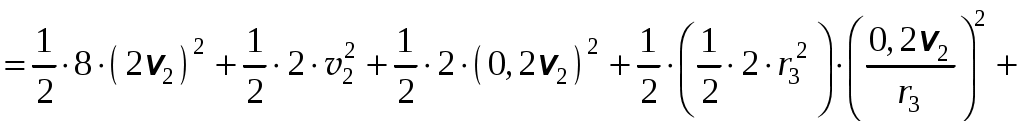
Рис.2. Расчетная схема к заданию Д4

3. Далее найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда тело 1 (к нему приложена сила F=f(t))пройдет путь м. Введем обозначения: – перемещение центра тяжести катка 3; – угол поворота шкива 4, – угол поворота шкива 5.

Тогда получим

;

;

;

;

;

;

;

.

Работы остальных сил равны нулю, так как точки, где приложены силы и , и – неподвижны, силы ,

---

перпендикулярны направлению перемещения соответственно тел 1, 2, а силы и приложены в центре скоростей тела 3 – точке .

Величины , , и необходимо выразить через заданное перемещение . При этом учитываем, что зависимости между перемещениями такие же как и между соответствующими скоростями. Таким образом,

;

;

;

.

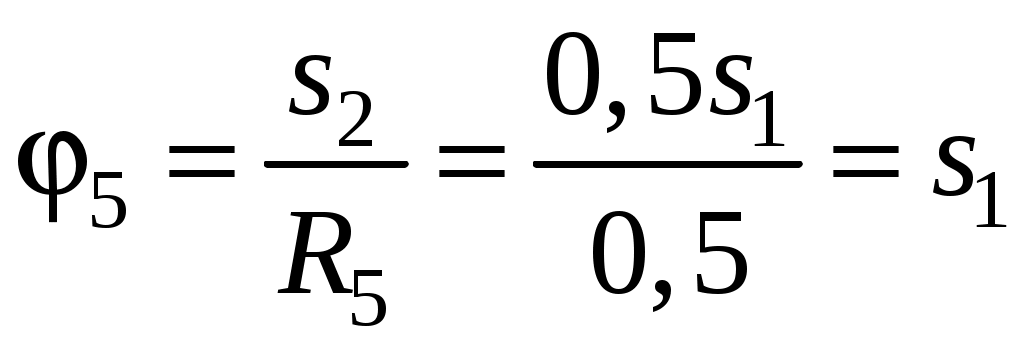При найденных значениях линейных у угловых перемещений для суммы вычисленных работ получим







Дж. (7)

Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что , получаем

,

откуда скорость тела 2 будет равна

м/с.

Зная и используя кинематические связи (4), находим остальные скорости:

---

рад/с;

м/с.

Ответ: м/с; рад/с; м/с.

Список использованной литературы

1. Черкасов В.Г., Петухова И.И. Теоретическая механика. Учебное пособие. Чита: ЗабГУ, 2015.

2. Бать М.И. Теоретическая механика в примерах и задачах. М.: Наука, 2007.

---

Смотрите также файлы

• Законом от 22 июля 2008 г. 123фз Технический регламент о требованиях пожарной безопасности.docx

• Занятие 10. Принятие решений на финансовых рынках, факторы появления финансовых пузырей.docx

• Практикум по курсу " Теоретические основы электротехники" для студентов электротехнических специальностей всех форм обучения.doc

• Законов о бюджетах Пенсионного фонда России, Фонда социального страхования рф, Федерального фомс на текущий год и плановый период, заполните нижеприведенную таблицу по данным.docx

• Философские идеи П. Чаадаева Славянофильство и западничество о путях развития России.docx