Билет №1

1. Понятие комплексного числа. Различные формы записи. Арифметические операции над комплексными числами, возведение в степень и извлечение корня.

Комплексное число – упорядоченная пара 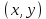вещественных чисел, первое из которых 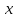называется действительной частью, а второе 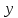– мнимой частью. ,

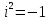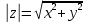
Два комплексных числа называются равными, есл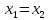и и 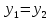. Комплексное число равно нулю, есл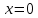и и .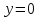

Формы записи:
1) По определению:
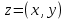
2) Алгебраическая:
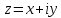
3) Тригонометрическая:
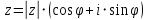
4) Показательная:

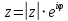
Арифметические операции
1) Сумма
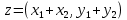2) Разность
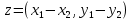3) Произведение
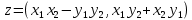4) Частное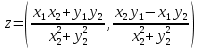


Возведение в степень По формуле Муавра:


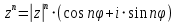
Извлечение корня По формуле Муавра:


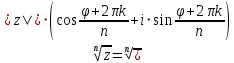
Справедливы следующие свойства:

---

1) 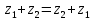(переместительное)
2) 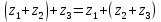(сочетательное)
3) 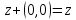(особая роль числа)
4) для каждого существует противоположное 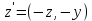, такое что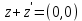
5) 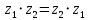(переместительное)
6) 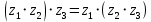(сочетательное)
7) 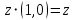(особая роль числа)
8) для любого числа существует обратное число 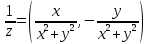, такое что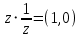
9) 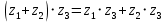(распределительное св-во произв. относительно суммы)

Комплексное число 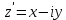называют сопряженным по отношению к числу

2. Возрастание (убывание) функции в точке. Достаточное условие возрастания (убывания) функции в точке.

Возрастание/убывание. Функция 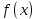возрастает (убывает) в точке 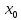, если найдётся такая 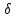-окрестность, в пределах которой ( ).

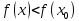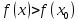Условие. Если функция дифференцируема в точке 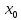и её производная в этой точке положительна (отрицательна), то функция возрастает (убывает) в точке .

---

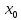Смотрите также файлы

• Краткий патан основным факультетам.doc

• Сведения о первоначальной вязке.docx

• Перечень практических заданий. Таблицаисходныхданных.docx

• Энергосбережение на предприятии.pdf

• Реферат по дисциплине Психиатрия и наркология для отработки пропyщенных лекций.docx