ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 30
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
отрицания (операция НЕ, инверсия), обозначаемая чертой над элементом.
По определению: а_|_ а_ j
a • a _ 0 1 _ 0 0 _ 1
Справедливы, например, такие соотношения:
a _ a
a + b _ a • b
a • b _ a + b
Функция в алгебре логики — выражение, содержащее элементы алгебры логики а, b, с и др., связанные операциями, определенными в этой алгебре. Логические высказывания (элементы алгебры логики а, b, с и др), входящие в запись выражения называют логическими переменными.
Примеры логических функций:
f (a, b, c) _ a + a • b • c + a + c
f(a,b,c) _ a•b+b•c+a•b•c
Для любой операции, определенной в алгебре логики существуют таблицы истинности -таблицы, в которых приведены значения операции в зависимости от значений высказываний над которыми выполняется данная операция.
Конъюнкция.
Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если
истинному высказыванию приписать значение '1', а ложному - '0', то сложное высказывание можно
назвать произведением.
Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания. Дизъюнкция
Э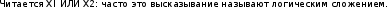
то сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.
Ч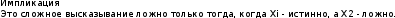
итается: если X1, то X2. При этом X1 - посылка, X2 - следствие.
Из ложной посылки может следовать ложное следствие и это можно считать верным: <если Киев - столица Франции>, то <2-квадрат 3>. Эквивалентности
В некоторых случаях сложное и длинное высказывание можно записать более коротким и простым без нарушения истинности исходного высказывания. Это можно выполнить с использованием некоторых эквивалентных соотношений.
Лекция 10. Основные логические элементы, их назначение и обозначение на схемах.
1. Логический элемент компьютера.
Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Логический элемент - простейшая структурная единицаЭВМ - выполняющая определенную логическую операцию над двоичными переменными согласно правилам алгебры логики.
Реализуется обычно на электронных приборах (полупроводниковых диодах, транзисторах) и резисторах, либо в виде интегральной микросхемы; имеет несколько входов для приема сигналов, соответствующих исходным переменным, и выход для выдачи сигнала, соответствующего результату операций. Для логических элементов приняты дискретные значения входных и выходных сигналов («0» и «1»).
2. Базовые логические элементы.
Базовые логические элементы ЭВМ реализуют три основные логические операции: конъюнктор - логический элемент «И» логическое умножение; дизъюнктор - логический элемент «ИЛИ» логическое сложение; инвертор - логический элемент «НЕ» инверсию.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс - логический смысл сигнала 1, нет импульса - 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
Конъюнктор
Конъюнкция - соответствует союзу «И», обозначается знаком л, иначе называется логическим умножением. Конъюнкция двух логических переменных истинна тогда и только тогда, когда обе переменные истинны.
Таблица истинностифункции логического умножения: А(0Д1;1)
Конъюнктор (логический элемент «И») - реализует операцию конъюнкции. На входы А и В логического элемента «И» подаются два сигнала (00, 01, 10, 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.
Дизъюнктор
Дизъюнкция - соответствует союзу «ИЛИ», обозначается знаком v, иначе называется логическим сложением. Дизъюнкция двух логических переменных истинна тогда, когда истинна хотя бы одна переменная
Таблица истинностифункции логического сложения: А(0.0.1.1)Дизъюнктор (логический элемент «ИЛИ») - реализует операцию дизъюнкции.
На входы А и В логического элемента «ИЛИ» подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
Инвертор - логический элемент «НЕ»
Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания или инверсией.
Логическое отрицание (инверсия) делает истинное выражение ложным и, наоборот, ложное -истинным.
Операцию логического отрицания (инверсию) над логическим высказыванием А A в алгебре логики принято обозначать —A.
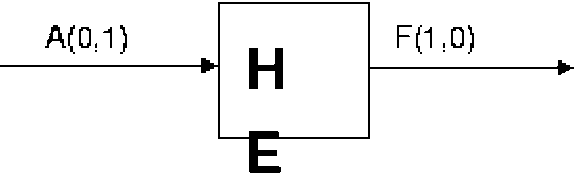
Таблица истинностифункции логического отрицания:
Инвертор - реализует операцию отрицания, или инверсию.
На вход А логического элемента подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.
Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов
.Лекция 11. Понятие алгоритма. Свойства алгоритма.
1. Что такое алгоритм.
Современный компьютер способен действовать только по формальным схемам, заготовленным для него человеком.
Поэтому, чтобы привлечь компьютер к исследованию объекта, процесса, явления или к "рутинной" обработке информации, прежде всего надо:
четко поставить задачу (разработать модель),
определить исходные данные, форму представления результатов.
далее необходимо создать алгоритм решения задачи и программу, которая будет понята компьютером.
Возникает классическая для информатики триада:
модель — алгоритм — программа
Во многих случаях этапы моделирования и алгоритмизации неотделимы друг от друга (например, при разработке модели производственного процесса).
Слово «алгоритм» произошло от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми, описавшего в IX веке правила выполнения вычислений с многозначными десятичными числами.
Работа по решению задач с использованием компьютера делится на несколько этапов. Основными этапами при этом является формализация и алгоритмизация решаемой задачи.
На этапе формализации задача переводится на язык математических формул, уравнений, отношений. После формализации описывается алгоритм решения задачи.
Алгоритм является одним из фундаментальных понятий в информатике.
Алгоритм - понятное и точное предписание (указание) исполнителю совершить определенную последовательность действий для достижения поставленной цели.
Исполнителем алгоритма может быть человек или автоматическое устройство - компьютеры, роботы, станки, спутники, сложная бытовая техника и даже детские игрушки. Каждый алгоритм создается в расчете на вполне конкретного исполнителя.
Применительно к компьютерам алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение результатов. Термин вычислительный процесс распространяется на обработку не только числовой информации, но и других видов информации (символьной, графической или звуковой).
Действия, которые может совершать исполнитель, называют
По определению: а_|_ а_ j
a • a _ 0 1 _ 0 0 _ 1
Справедливы, например, такие соотношения:
a _ a
a + b _ a • b
a • b _ a + b
Функция в алгебре логики — выражение, содержащее элементы алгебры логики а, b, с и др., связанные операциями, определенными в этой алгебре. Логические высказывания (элементы алгебры логики а, b, с и др), входящие в запись выражения называют логическими переменными.
Примеры логических функций:
f (a, b, c) _ a + a • b • c + a + c
f(a,b,c) _ a•b+b•c+a•b•c
Для любой операции, определенной в алгебре логики существуют таблицы истинности -таблицы, в которых приведены значения операции в зависимости от значений высказываний над которыми выполняется данная операция.
Конъюнкция.
Поскольку таблица истинности для конъюнкции совпадает с таблицей умножения, если
истинному высказыванию приписать значение '1', а ложному - '0', то сложное высказывание можно
назвать произведением.
| Xi | X2 | fl(Xi,X2) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания. Дизъюнкция
Э
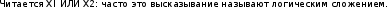
то сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.
Ч
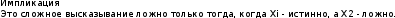итается: если X1, то X2. При этом X1 - посылка, X2 - следствие.Из ложной посылки может следовать ложное следствие и это можно считать верным: <если Киев - столица Франции>, то <2-квадрат 3>. Эквивалентности
В некоторых случаях сложное и длинное высказывание можно записать более коротким и простым без нарушения истинности исходного высказывания. Это можно выполнить с использованием некоторых эквивалентных соотношений.
Лекция 10. Основные логические элементы, их назначение и обозначение на схемах.
-
Логический элемент компьютера. -
Базовые логические элементы.
1. Логический элемент компьютера.
Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Логический элемент - простейшая структурная единицаЭВМ - выполняющая определенную логическую операцию над двоичными переменными согласно правилам алгебры логики.
Реализуется обычно на электронных приборах (полупроводниковых диодах, транзисторах) и резисторах, либо в виде интегральной микросхемы; имеет несколько входов для приема сигналов, соответствующих исходным переменным, и выход для выдачи сигнала, соответствующего результату операций. Для логических элементов приняты дискретные значения входных и выходных сигналов («0» и «1»).
2. Базовые логические элементы.
Базовые логические элементы ЭВМ реализуют три основные логические операции: конъюнктор - логический элемент «И» логическое умножение; дизъюнктор - логический элемент «ИЛИ» логическое сложение; инвертор - логический элемент «НЕ» инверсию.
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс - логический смысл сигнала 1, нет импульса - 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
Конъюнктор
Конъюнкция - соответствует союзу «И», обозначается знаком л, иначе называется логическим умножением. Конъюнкция двух логических переменных истинна тогда и только тогда, когда обе переменные истинны.
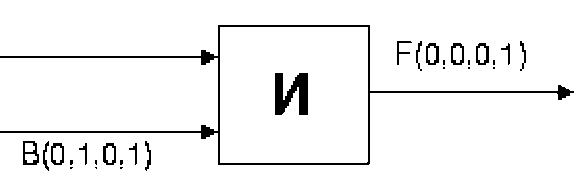 A | B | F=A/\B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблица истинностифункции логического умножения: А(0Д1;1)
Конъюнктор (логический элемент «И») - реализует операцию конъюнкции. На входы А и В логического элемента «И» подаются два сигнала (00, 01, 10, 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.
Дизъюнктор
Дизъюнкция - соответствует союзу «ИЛИ», обозначается знаком v, иначе называется логическим сложением. Дизъюнкция двух логических переменных истинна тогда, когда истинна хотя бы одна переменная
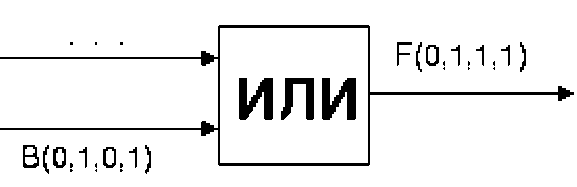| .  A | B | F=AvB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Таблица истинностифункции логического сложения: А(0.0.1.1)Дизъюнктор (логический элемент «ИЛИ») - реализует операцию дизъюнкции.
На входы А и В логического элемента «ИЛИ» подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
Инвертор - логический элемент «НЕ»
Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания или инверсией.
Логическое отрицание (инверсия) делает истинное выражение ложным и, наоборот, ложное -истинным.
Операцию логического отрицания (инверсию) над логическим высказыванием А A в алгебре логики принято обозначать —A.
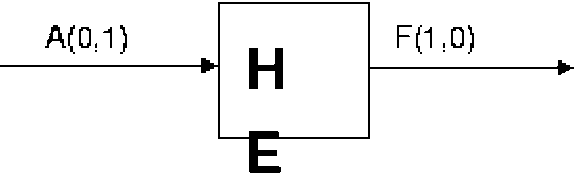
Таблица истинностифункции логического отрицания:
| A | F=—A |
| 0 | 1 |
| 1 | 0 |
Инвертор - реализует операцию отрицания, или инверсию.
На вход А логического элемента подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.
Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов
.Лекция 11. Понятие алгоритма. Свойства алгоритма.
-
Что такое алгоритм. -
Свойства алгоритмов. -
Виды алгоритмов. -
Формы записи алгоритмов.
1. Что такое алгоритм.
Современный компьютер способен действовать только по формальным схемам, заготовленным для него человеком.
Поэтому, чтобы привлечь компьютер к исследованию объекта, процесса, явления или к "рутинной" обработке информации, прежде всего надо:
четко поставить задачу (разработать модель),
определить исходные данные, форму представления результатов.
далее необходимо создать алгоритм решения задачи и программу, которая будет понята компьютером.
Возникает классическая для информатики триада:
модель — алгоритм — программа
Во многих случаях этапы моделирования и алгоритмизации неотделимы друг от друга (например, при разработке модели производственного процесса).
Слово «алгоритм» произошло от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми, описавшего в IX веке правила выполнения вычислений с многозначными десятичными числами.
Работа по решению задач с использованием компьютера делится на несколько этапов. Основными этапами при этом является формализация и алгоритмизация решаемой задачи.
На этапе формализации задача переводится на язык математических формул, уравнений, отношений. После формализации описывается алгоритм решения задачи.
Алгоритм является одним из фундаментальных понятий в информатике.
Алгоритм - понятное и точное предписание (указание) исполнителю совершить определенную последовательность действий для достижения поставленной цели.
Исполнителем алгоритма может быть человек или автоматическое устройство - компьютеры, роботы, станки, спутники, сложная бытовая техника и даже детские игрушки. Каждый алгоритм создается в расчете на вполне конкретного исполнителя.
Применительно к компьютерам алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение результатов. Термин вычислительный процесс распространяется на обработку не только числовой информации, но и других видов информации (символьной, графической или звуковой).
Действия, которые может совершать исполнитель, называют