Файл: Лабораторная работа 3 Спектр излучения атомарного водорода Цель работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 8
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 3
«Спектр излучения атомарного водорода»
Цель работы:
-
Знакомство с планетарной и квантовой моделями атома при моделировании процесса испускания электромагнитного излучения возбужденными атомами водорода. -
Экспериментальное подтверждение закономерностей формирования линейчатого спектра атомарного водорода при низких давлениях. -
Экспериментальное определение постоянной Ридберга.
Планетарная модель атома водорода
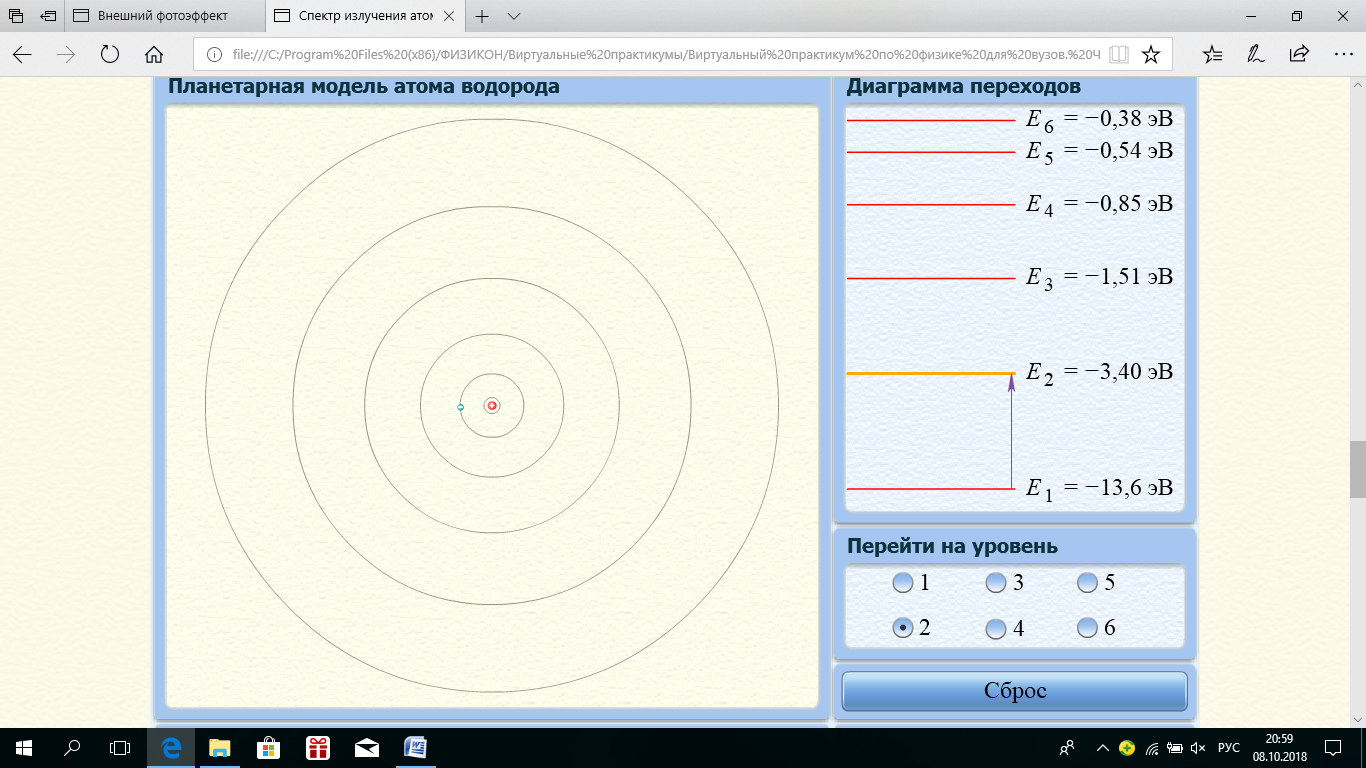
Диаграмма уровней энергии атома водорода

Таблица 2.
Результаты измерений. Серия Бальмера . n0 = 2 .
| Номер линии i | 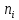 | 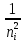 | 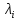 , мкм , мкм | 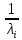 , мкм-1 , мкм-1 |
| 1 | 3 | 0,111 | 0,656 | 1,524 |
| 2 | 4 | 0,0625 | 0,486 | 2,058 |
| 3 | 5 | 0,04 | 0,434 | 2,304 |
| 4 | 6 | 0,028 | 0,410 | 2,439 |
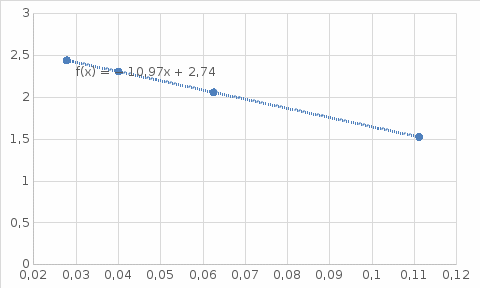
График зависимости обратной длины волны 1/λ от обратного квадрата квантового числа 1/n2
Расчетная формула:
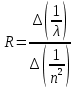
Среднее значение постоянной Ридберга по графику можно взять из уравнения тренда:
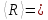 10,987 *
10,987 * 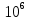
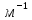 .
.Формула для расчета абсолютной погрешности измерения постоянной Ридберга:
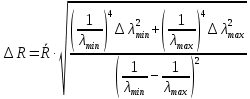 = 10,987 *
= 10,987 * 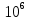 *
* 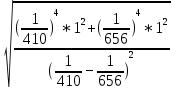 = 10,987 *
= 10,987 * 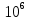 * 0,02 = 0,22 *
* 0,02 = 0,22 * 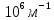 .
.где
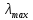 и
и 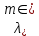 - соответственно максимальное и минимальное значения длины волны излучения в эксперименте,
- соответственно максимальное и минимальное значения длины волны излучения в эксперименте, 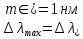 -- абсолютные погрешности измерения длины волны.
-- абсолютные погрешности измерения длины волны. Абсолютная погрешность измерения постоянной Ридберга:
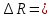 0,22 *
0,22 * 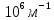
Окончательная запись результата:
R = (10,99 ± 0,22) *
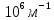 .
.Сравнение полученного результата с табличным.
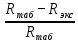 * 100 % =
* 100 % = 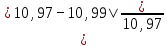 * 100 % = 0,2 %.
* 100 % = 0,2 %.Aнализ графика и вывод: исследовано экспериментальное подтверждение закономерностей формирования линейчатого спектра атомарного водорода при низких давлениях. Построен график зависимости ависимости обратной длины волны 1/λ от обратного квадрата квантового числа 1/n2, который оказался линейной функцией. По тангенсу угла наклона графика определена постоянная Ридберга. Полученное значение незначительно отличается от табличного, погрешность составляет 0,2 %.
