Вариант № 0
Задание № 1 – Измерение расходов жидкостей и газов по скорости

Задание выполнена в соответствии с ГОСТ 8.361-79. ГСИ


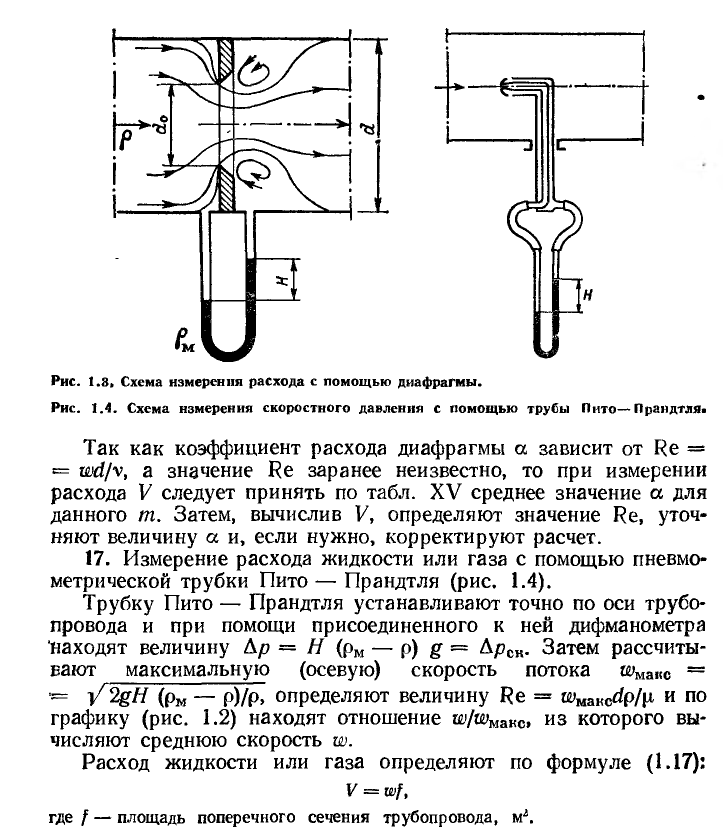
Рисунок 1 ‒ Схема измерения скорости жидкости или газа трубкой
Пито-Прандтля
Трубку Пито-Прандтля устанавливаем точно по оси трубопровода и при помощи присоединенного к ней дифманометра находим величину разности динамического и статического давлений:

(1)

Затем рассчитываем максимальную (осевую) скорость потока:

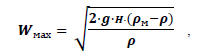(2)

Определяем число Рейнольдса:

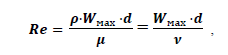(3)

где d ‒ внутренний диаметр трубопровода.

По графику


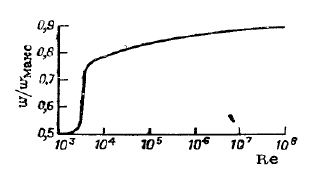
Рисунок 2 – Зависимость отношения средней скорости потока

к его максимальной скорости от

находим величину средней скорости W потока. Расход жидкости или газа определяем по формуле:

(4)
Задача № 1
Исходные данные:

Внешний диаметр трубопровода ‒ ???? = 1000 мм, измеряется стальной рулеткой с миллиметровыми делениями по ГОСТ 7502-80. Погрешность измерений составляет ± 0,5 мм

Толщина стенки ???? трубы равна 20 мм и измеряется ультразвуковым толщиномером с погрешностью ± 2%

Коэффициент гидравлического сопротивления трубопровода ???? = 0,02

По трубопроводу транспортируется углеводородная жидкость плотностью ???? = 700 кг/м3 и динамической вязкостью ???? = 1,45 ·10^-3 Па ·с

Измерение проводят с помощью трубки Пито-Прандтля, вторичным прибором является дифференциальный манометр, заправленный ртутью. Высота Н = 100 мм.

---

Расчет

1. 
   Переводим все единицы величин в систему СИ
   
2. 
   Определим величину разности динамического и статического давлений, подставив числовые значения в формулу (1):
   

Δ???? = 0,1·9,8· (13600 – 700) = 12642 Па

3. 
   Определим максимальную (осевую) скорость потока, подставив числовые значения в формулу (2):
   

????мах = 0,84·√18,06 = 3,399 м/с
???????? = 0,84, так как ???? = 0,02

4. 
   Определим число Рейнольдса, подставив числовые значения в
   формулу (3):
   

???????? = (700·3,399·(1,0−2·0,02))/1,45·10^-3 = 2284.12/1,45·10^-3 = 1,57 ·10⁶

5. 
   С помощью графика (рисунок 2) определим среднюю скорость потока:
   

????/????мах = 0,87

6. 
   Определим расход жидкости, подставив числовые значения в
   формулу (4):
   

???? = 0,785·(1,0−2·0,02)²·0,87∙3,399 = 0,785·0,9216·0,87·3,399 = 2,138 м³/с
Задача № 2
Исходные данные:

Внешний диаметр трубопровода ‒ d = 1000 мм

Погрешность измерений составляет ± 0,5 мм

Толщина стенки с трубы равна 20 мм с погрешностью ± 2%

Коэффициент гидравлического сопротивления трубопровода = 0,02.

По трубопроводу транспортируется углеводородный газ с относительной молекулярной массой m = 16 и температурой 20⁰С под давлением P = 2,5 МПа и динамической вязкостью =11,2 ·10^-6 Па ·с

Фактор сжимаемости газа z = 0,95

Измерение проводят с помощью трубки Пито-Прандтля, вторичным прибором является дифференциальный манометр, заправленный спиртом, плотность которого при 20⁰С равна P_м = 721 кг/м³. Высота Н= 200 мм.
Расчет

1. 
   Переводим все единицы величин в систему СИ.
   
2. 
   Определим плотность газа в рабочих условиях:
   

???? = (????·????)/(8314·????·????) = (16·2,5·10⁶)/(8314·293·0,95) = (40·10⁶)/(2314201,9) = 40/2,31 = 17,31 кг/м³

3. 
   Определим величину разности динамического и статического давлений, подставив числовые значения в формулу (1):
   

Δ???? = 0,2·9,8·(721 – 17,31) = 1,96·703,69 = 1379,23 Па

4. 
   Определим максимальную (осевую) скорость потока, подставив числовые значения в формулу (2):
   

????мах = 0,84·√(1379,23/17,31) = 0,8·√79,67 = 0,8·8,926 = 7,14 м/с
???????? = 0,84, так как ???? = 0,02

5. 
   Определим число Рейнольдса, подставив числовые значения в
   формулу (3):
   

???????? = 17,31·7,14·(1,0−2·0,02)/(11,2·10^-6) = 1,06·10⁷

6. 
   С помощью графика (рисунок 2) определим среднюю скорость потока:
   

????/????мах = 0,88

7. 
   Определим расход газа в пластовых условиях, подставив числовые значения в формулу (4):
   

---

???? = 0,785·(1,0−2·0,02)²·0,88∙7,14 = 0,785∙0,9216∙0,88∙7,14 = 4,545 м³/с
или ???? = 4,545·17,31 = 78,67 кг/с

8. 
   Определим расход газа при нормальных условиях:
   

????_ну = (????·????_ну)/(8314·????_ну·????) = (16·1.01·10⁵)/(8314·293·0,95) = 16,16/23,142 = 0,698 кг/м³
????_ну = ????/????_ну = 78,67/0,698 = 117,45 м³/с

Задание № 2 – Определение погрешности измерения расхода

При установке первичного преобразователя на оси трубы определения отношения скорости на оси трубы к средней скорости среднее квадратичное отклонение измерений расхода определяется по формуле:

(5)


При определении отношения по графику на рисунке 2:
0,02, = 0.
Погрешность определения площади измерительного сечения зависит от применяемых метода и средств измерения.

При непосредственном измерении внутреннего диаметра трубы среднее квадратичное отклонение определения площади измерительного сечения вычисляем по формуле:
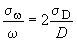, (6)
где ‒ среднее квадратичное отклонение измерений площади измерительного сечения, м ;

‒ диаметр измерительного сечения, м;

‒ среднее квадратичное отклонение измерений диаметра измерительного сечения, м.

При измерении наружного периметра трубы и толщины стенки среднее квадратичное отклонение определения площади измерительного сечения вычисляем по формуле:
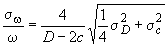, (7)
где

---

‒ толщина стенки трубы, м;

‒ среднее квадратичное отклонение измерений толщины стенки трубы, м.

Среднее квадратичное отклонение измерений скорости определяем по формуле:
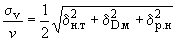, (8)
где ‒ погрешность напорной трубки;

‒ погрешность дифманометра;

‒ погрешность регистрирующего прибора.

Предел допускаемой погрешности измерения расхода с доверительной вероятностью 0,95 определяем по формуле:
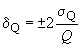, (9)

где ‒ предел допускаемой погрешности измерения расхода;

‒ среднее квадратичное отклонение измерений расхода, м /c.
Задача № 1
Определить погрешность в случае измерения расхода жидкости в трубопроводе диаметром 1000 мм и толщиной стенки 20 мм.

Градуировочный коэффициент напорной трубки известен с погрешностью ± 1%. В качестве вторичной аппаратуры применяют дифманометр типа ДМИ класса 1,6; может применяться вторичный регистрирующий прибор типа ВФС класса 0,5.
Расчет

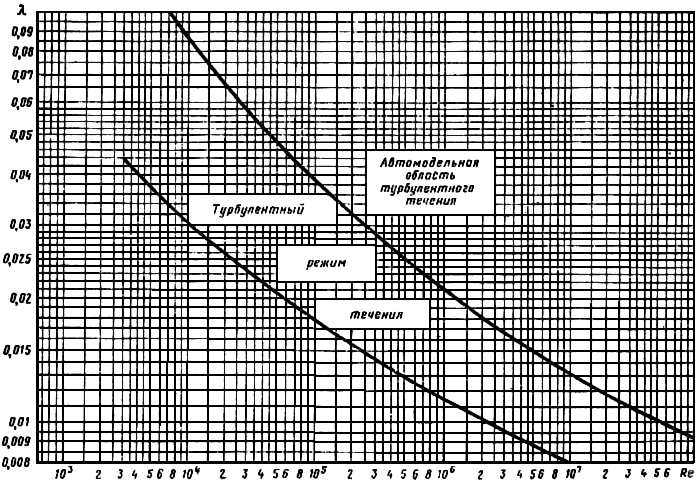
Рисунок 3 – График определения режима течения
Для данных условий Re = 1,57·10⁶ по графику (рисунок 3) определяим режим течения – автомодельный

При определении отношения ????/????мах по графику (рисунок 2):



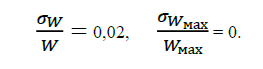
Погрешность определения площади измерительного сечения зависит от применяемых метода и средств измерения.

---

Поскольку перерыв в подаче жидкости не допускается, площадь поперечного сечения определяют по результатам измерения наружного периметра трубы. Инструмент ‒ стальная рулетка с миллиметровыми делениями по ГОСТ 7502-80. Погрешность измерений составит ± 0,5 мм.

При доверительной вероятности 0,95 абсолютное среднее квадратическое отклонение результатов измерений равно половине доверительного интервала:
D = 0,5² = 0,25 мм
Толщина стенки трубы равна 20 мм и измеряется ультразвуковым толщиномером с погрешностью ± 2%, абсолютное среднее квадратичное отклонение равно:
c = 20·0,02 = 0,4 мм
Согласно формуле (7):

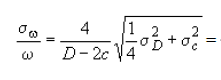-2·20)) ·√1/4·(0.25)²+0,4² = 4/960 · √0,015625+0.16 = 0,004166 · 0,419 =17,4·10^-4
Погрешность измерения локальной скорости зависит от погрешности градуировочного коэффициента напорной трубки и класса точности вторичной аппаратуры.

Среднее квадратичное отклонение измерений скорости определим, подставив числовые значения в формулу (8):
1/2·√0,01²+0,016²+0,005² = 0,5·√0,0001+0,000256+0,000025 = 0,5·0,051 = 0,026
Подставляя все составляющие погрешности измерения расхода в формулу (5), получим среднее квадратичное отклонение определения расхода для рассматриваемого случая:

√0,026²+(17,4·10^-4)²+0,02² = √0,000676+0,0000030276+0,0004 = 0,0328
Тогда, предел допускаемой погрешности измерения расхода с доверительной вероятностью 0,95 равен:

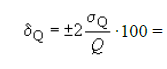0,0328·± 2·100 = ± 6,56 %

---

Смотрите также файлы

• Отчет о прохождении производственной практики студента по специальности 09. 02. 03 Программирование в компьютерных системах.docx

• 1 характеристики педагогики как науки.docx

• урока 14 Тема урока Градусная сетка Цели Содержательная (предметные результаты).docx

• Планконспект проведения занятий в системе подготовки личного состава дежурных караулов по охране труда с личным составом дежурных караулов 11 пожарноспасательной части Тема 5 Требования правил охраны труда при проведении практических занятий.doc

• Самостоятельная работа по теме 4 Задание Сравните понятия преподавание.docx