ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 15
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
,
который сходится, так как
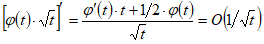 при ;
при ;
следовательно, второе слагаемое есть тоже при .
при .
Итак, имеем:
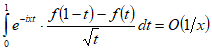 при . (1.11)
при . (1.11)
Из (1.8), (1.9), (1.10) получаем искомое асимптотическое представление:
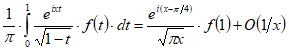 при .(1.12)
при .(1.12)
Из этой формулы, переходя к сопряженным величинам, найдем еще:
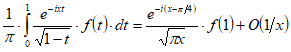 при .(1.13)
при .(1.13)
Формулы (1.12) и (1.13) верны и для комплекснозначных функций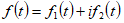 .
.
Вывод асимптотической формулы для Jn(x)
Заменяя на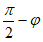 , получим:
, получим:
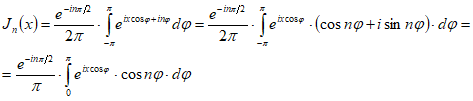
(учитывая, что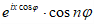 есть четная функция от , а
есть четная функция от , а 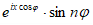 есть нечетная функция от ). Подстановка дает:
есть нечетная функция от ). Подстановка дает:
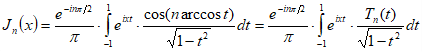 ,
,
где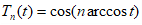 есть, очевидно, полином n-й степени (полином Чебышева), так как из формулы Муавра видно, что
есть, очевидно, полином n-й степени (полином Чебышева), так как из формулы Муавра видно, что 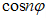 есть полином n-й степени относительно . Но
есть полином n-й степени относительно . Но
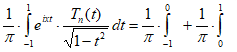
и, заменяя в первом из этих интегралов на , получим:
Так как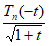 и
и 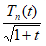 на имеют производные всех порядков, то к двум последним интегралам применимы формулы (1.12) и (1.13), и мы получаем:
на имеют производные всех порядков, то к двум последним интегралам применимы формулы (1.12) и (1.13), и мы получаем:
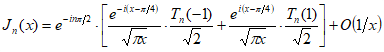 ;
;
но
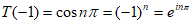 ;
; 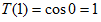 , следовательно,
, следовательно,
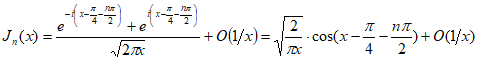 .
.
Итак, имеем искомое асимптотическое представление бесселевой функции первого рода с целым индексом для больших значений аргумента:
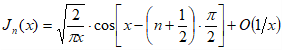 при .(1.14)
при .(1.14)
Эта формула показывает, что с точностью до слагаемого порядка является затухающей гармоникой с волной постоянной длины и амплитудой, убывающей обратно пропорционально квадратному корню из абсциссы.
В частности,
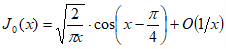 при ; (1.15)
при ; (1.15)
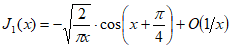 при . (1.16)
при . (1.16)
Графики этих функций изображены ни рис1.
Рассмотрим несколько примеров решения уравнения Бесселя.
. Найти решение уравнения Бесселя при
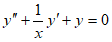 ,
,
удовлетворяющее начальным условиям при , и .
Решение.
На основании формулы 5 находим одно частное решение:
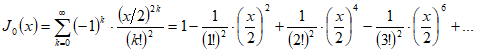 .
.
. Найти одно из решений уравнения:
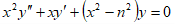 ,
, 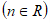 .
.
Решение.
Сделаем замену
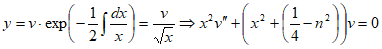 .
.
При получим:
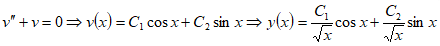 .
.
При будем искать решение в виде обобщенного степенного ряда:
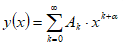 .
.
Уравнение на имеет вид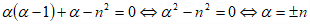 ;
;
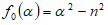
, , , , поэтому
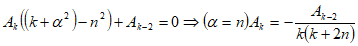 ,
,
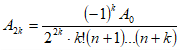 ,
, 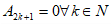 .
.
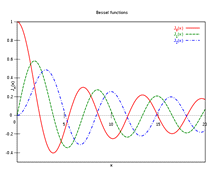
Рис.1.1 График распределения интенсивности функции бесселя 0,1и2 порядков.
Свойства
Как и в случае с плоской волной, настоящий пучок Бесселя не может быть создан, поскольку он неограничен и потребует бесконечного количества энергии. Тем не менее, могут быть сделаны достаточно хорошие приближения, и они важны во многих оптических приложениях, поскольку они практически не проявляют дифракции на ограниченном расстоянии. Приближения к пучкам Бесселя выполняются на практике либо путем фокусировки гауссова пучка с помощью аксиконовой линзы для получения пучка Бесселя–Гаусса, с использованием осесимметричных дифракционных решеток, либо путем размещения узкой кольцевой апертуры в дальнем поле. Пучки Бесселя высокого порядка могут генерироваться спиральными дифракционными решетками.
На рисунках 1 и 2 представлены реальные изображения Бесселевых пучков, формируемых аксиконом на экране. Исходные данные: источником света (параллельного пучка) является зеленый лазер. Диаметр падающего пучка в обоих опытах 4 мм, баланс белого 127 х 127 мм. Угол аксикона α=20°. Опыт показывает, что толщина кольца на экране остается постоянной (2 мм), а диаметр растет по мере удаления экрана от аксикона: на рис. 2 аксикон расположен на расстоянии L= 228.6 мм и диаметр кольца на экране составляет 73.66 мм, на рис.3 – L=355.6 мм и диаметр равен 114.3 мм.
Аксиконы
Аксиконы – осесимметричные оптические линзы, одна поверхность которых плоская, а вторая – коническая. Главные параметры аксикона (рис. 1) – угол раствора конуса и угол α между образующей поверхностью и основанием. В отличие от собирающих линз (плосковыпуклых, двояковыпуклых и асферических), предназначенных для фокусировки пучка, исходящего от точечного источника в одну точку, лежащую на главной оптической оси, при прохождении пучка через аксикон на экране наблюдается тонкое кольцо, формирование которого происходит за счет интерференции. При использовании аксиконов также происходит формирование Бесселевых пучков с протяженной глубиной фокусировки. Такие пучки оказываются
достаточно полезным при регулировке уровней, выравнивании протяженных объектов, а также при захвате частиц (оптические ловушки). Бесселевы пучки образуются в области перекрытия пучков
Свойства пучков Бесселя делают их чрезвычайно полезными для оптического пинцета, поскольку узкий пучок Бесселя будет сохранять требуемое свойство плотной фокусировки на относительно длинном участке пучка и даже при частичном перекрытии выщипываемыми частицами диэлектрика. Аналогично, манипулирование частицами с помощью акустического пинцета было достигнуто с помощью луча Бесселя, который рассеивает и создает силу излучения, возникающую в результате обмена акустическим импульсом между волновым полем и частицей, расположенной вдоль его пути.
Математическая функция, описывающая балку Бесселя, является решением дифференциального уравнения Бесселя, которое само по себе возникает из сепарабельных решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических координатах. Фундаментальный пучок Бесселя нулевого порядка имеет максимум амплитуды в начале координат, в то время как пучок Бесселя высокого порядка (ХОББ) имеет осевую фазовую особенность вдоль оси пучка; амплитуда там равна нулю. Пучок Хоббса может быть вихревого (геликоидального) или невихревого типа.
Ускорение
В 2012 году было теоретически доказано и экспериментально продемонстрировано, что при специальной манипуляции с их начальной фазой пучки Бесселя могут ускоряться по произвольным траекториям в свободном пространстве. Эти балки можно рассматривать как гибриды, которые сочетают симметричный профиль стандартной балки Бесселя со свойством самоускорения балки Эйри и ее аналогов. Предыдущие попытки создания ускоряющих пучков Бесселя включали пучки со спиральными и синусоидальными траекториями, а также ранние попытки создания пучков с кусочно-прямыми траекториями.
Распространяясь, луч Эйри не подвергается дифракции, то есть не расплывается. Для этого луча характерно свободное ускорение: по мере распространения он отклоняется от первоначального направления, формируя дугу параболы.
Компенсация затухания
При прохождении лучей через материалы могут возникать потери, что приведет к ослаблению интенсивности луча. Общим свойством пучков без дифрагирования (или инвариантных к распространению), таких как пучок Эйри и пучок Бесселя, является способность управлять продольной огибающей интенсивности пучка без существенного изменения других характеристик пучка. Это может быть использовано для создания пучков Бесселя, интенсивность
которых увеличивается по мере их перемещения, и может быть использовано для нейтрализации потерь, тем самым поддерживая луч постоянной интенсивности при его распространении.
Применение
Визуализация и микроскопия
В световой флуоресцентной микроскопии недифрагирующие (или инвариантные к распространению) лучи используются для получения очень длинных и однородных световых полос, размер которых существенно не изменяется по всей длине. Также было показано, что свойство самовосстановления лучей Бесселя обеспечивает улучшенное качество изображения на глубине, поскольку форма луча меньше искажается после прохождения через рассеивающую ткань, чем у гауссова луча. Световая микроскопия на основе пучка Бесселя была впервые продемонстрирована в 2010 году, но с тех пор последовало много изменений. В 2018 году было показано, что использование компенсации затухания может быть применено к световой микроскопии на основе пучка Бесселя и может обеспечить получение изображений на больших глубинах в биологических образцах.
Подводные системы звуковидения и акустическая голография
Большое внимание уделяется в настоящее время акустической голографии. Акустические системы подводного видения имеют ряд преимуществ перед системами прямого оптического видения и гидролокационными системами обычного типа при наблюдениях в водной среде. Оптическое видение ограничивается сравнительно небольшими дальностями, особенно в мутной воде, а гидролокационные системы не обеспечивают детальной информации о цели. Акустическая голография позволяет создать систему видения, на которую мало влияет турбулентность и мутность воды и которая может воспроизводить изображения подводных объектов в сравнительно большом угле поля зрения при большей дальности видения по сравнению с оптическими системами.
Акустическая жидкость
Пучки Бесселя являются хорошим кандидатом для выборочного захвата из-за концентрических окружностей максимального и минимального давления в поперечных плоскостях.
Акустические линзы
устройство для фокусировки звука путём изменения длины пути, проходимого акустич. волной, и её преломления (рефракции) на граничных поверхностях. Свойства Л. определяются свойствами материала линзы и окружающей её среды и формой преломляющих поверхностей линзы. Показатель преломления Л. n=с1/с2, где с2 и с1 — скорости волн в материале линзы и в окружающей среде соответственно. При n>1 (с2<с1) собирающая линза имеет хотя бы одну выпуклую преломляющую поверхность и наз. замедляющей. При n<1 (c2>c1) собирающая Л. имеет хотя бы одну вогнутую преломляющую поверхность в наз. ускоряющей. Материал для Л. должен обладать миним. затуханием и волновым сопротивлением, близким к волновому сопротивлению окружающей среды. Л. изготавливают из тв. материалов, жидкостей и газов. В последних двух случаях используют оболочку, обеспечивающую макс. прохождение энергии и незначит. отклонение лучей при преломлении. Ускоряющие Л. обладают меньшими сферич. аберрациями, чем замедляющие.
который сходится, так как
следовательно, второе слагаемое есть тоже
Итак, имеем:
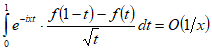 при . (1.11)
при . (1.11)Из (1.8), (1.9), (1.10) получаем искомое асимптотическое представление:
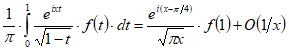 при .(1.12)
при .(1.12)Из этой формулы, переходя к сопряженным величинам, найдем еще:
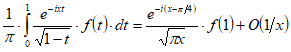 при .(1.13)
при .(1.13)Формулы (1.12) и (1.13) верны и для комплекснозначных функций
Вывод асимптотической формулы для Jn(x)
Заменяя на
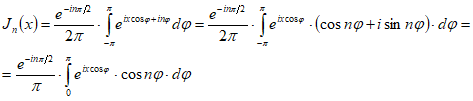
(учитывая, что
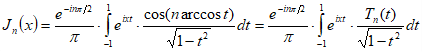 ,
,где
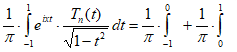
и, заменяя в первом из этих интегралов на , получим:
Так как
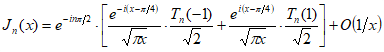 ;
;но
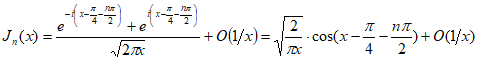 .
.Итак, имеем искомое асимптотическое представление бесселевой функции первого рода с целым индексом для больших значений аргумента:
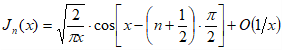 при .(1.14)
при .(1.14)Эта формула показывает, что с точностью до слагаемого порядка является затухающей гармоникой с волной постоянной длины и амплитудой, убывающей обратно пропорционально квадратному корню из абсциссы.
В частности,
Графики этих функций изображены ни рис1.
Рассмотрим несколько примеров решения уравнения Бесселя.
. Найти решение уравнения Бесселя при
удовлетворяющее начальным условиям при , и .
Решение.
На основании формулы 5 находим одно частное решение:
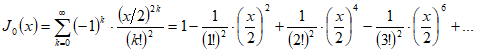 .
.. Найти одно из решений уравнения:
Решение.
Сделаем замену
При получим:
При будем искать решение в виде обобщенного степенного ряда:
Уравнение на имеет вид
, , , , поэтому
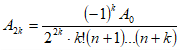 ,
, 
Рис.1.1 График распределения интенсивности функции бесселя 0,1и2 порядков.
Свойства
Как и в случае с плоской волной, настоящий пучок Бесселя не может быть создан, поскольку он неограничен и потребует бесконечного количества энергии. Тем не менее, могут быть сделаны достаточно хорошие приближения, и они важны во многих оптических приложениях, поскольку они практически не проявляют дифракции на ограниченном расстоянии. Приближения к пучкам Бесселя выполняются на практике либо путем фокусировки гауссова пучка с помощью аксиконовой линзы для получения пучка Бесселя–Гаусса, с использованием осесимметричных дифракционных решеток, либо путем размещения узкой кольцевой апертуры в дальнем поле. Пучки Бесселя высокого порядка могут генерироваться спиральными дифракционными решетками.
На рисунках 1 и 2 представлены реальные изображения Бесселевых пучков, формируемых аксиконом на экране. Исходные данные: источником света (параллельного пучка) является зеленый лазер. Диаметр падающего пучка в обоих опытах 4 мм, баланс белого 127 х 127 мм. Угол аксикона α=20°. Опыт показывает, что толщина кольца на экране остается постоянной (2 мм), а диаметр растет по мере удаления экрана от аксикона: на рис. 2 аксикон расположен на расстоянии L= 228.6 мм и диаметр кольца на экране составляет 73.66 мм, на рис.3 – L=355.6 мм и диаметр равен 114.3 мм.
Аксиконы
Аксиконы – осесимметричные оптические линзы, одна поверхность которых плоская, а вторая – коническая. Главные параметры аксикона (рис. 1) – угол раствора конуса и угол α между образующей поверхностью и основанием. В отличие от собирающих линз (плосковыпуклых, двояковыпуклых и асферических), предназначенных для фокусировки пучка, исходящего от точечного источника в одну точку, лежащую на главной оптической оси, при прохождении пучка через аксикон на экране наблюдается тонкое кольцо, формирование которого происходит за счет интерференции. При использовании аксиконов также происходит формирование Бесселевых пучков с протяженной глубиной фокусировки. Такие пучки оказываются
достаточно полезным при регулировке уровней, выравнивании протяженных объектов, а также при захвате частиц (оптические ловушки). Бесселевы пучки образуются в области перекрытия пучков
Свойства пучков Бесселя делают их чрезвычайно полезными для оптического пинцета, поскольку узкий пучок Бесселя будет сохранять требуемое свойство плотной фокусировки на относительно длинном участке пучка и даже при частичном перекрытии выщипываемыми частицами диэлектрика. Аналогично, манипулирование частицами с помощью акустического пинцета было достигнуто с помощью луча Бесселя, который рассеивает и создает силу излучения, возникающую в результате обмена акустическим импульсом между волновым полем и частицей, расположенной вдоль его пути.
Математическая функция, описывающая балку Бесселя, является решением дифференциального уравнения Бесселя, которое само по себе возникает из сепарабельных решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических координатах. Фундаментальный пучок Бесселя нулевого порядка имеет максимум амплитуды в начале координат, в то время как пучок Бесселя высокого порядка (ХОББ) имеет осевую фазовую особенность вдоль оси пучка; амплитуда там равна нулю. Пучок Хоббса может быть вихревого (геликоидального) или невихревого типа.
Ускорение
В 2012 году было теоретически доказано и экспериментально продемонстрировано, что при специальной манипуляции с их начальной фазой пучки Бесселя могут ускоряться по произвольным траекториям в свободном пространстве. Эти балки можно рассматривать как гибриды, которые сочетают симметричный профиль стандартной балки Бесселя со свойством самоускорения балки Эйри и ее аналогов. Предыдущие попытки создания ускоряющих пучков Бесселя включали пучки со спиральными и синусоидальными траекториями, а также ранние попытки создания пучков с кусочно-прямыми траекториями.
Распространяясь, луч Эйри не подвергается дифракции, то есть не расплывается. Для этого луча характерно свободное ускорение: по мере распространения он отклоняется от первоначального направления, формируя дугу параболы.
Компенсация затухания
При прохождении лучей через материалы могут возникать потери, что приведет к ослаблению интенсивности луча. Общим свойством пучков без дифрагирования (или инвариантных к распространению), таких как пучок Эйри и пучок Бесселя, является способность управлять продольной огибающей интенсивности пучка без существенного изменения других характеристик пучка. Это может быть использовано для создания пучков Бесселя, интенсивность
которых увеличивается по мере их перемещения, и может быть использовано для нейтрализации потерь, тем самым поддерживая луч постоянной интенсивности при его распространении.
Применение
Визуализация и микроскопия
В световой флуоресцентной микроскопии недифрагирующие (или инвариантные к распространению) лучи используются для получения очень длинных и однородных световых полос, размер которых существенно не изменяется по всей длине. Также было показано, что свойство самовосстановления лучей Бесселя обеспечивает улучшенное качество изображения на глубине, поскольку форма луча меньше искажается после прохождения через рассеивающую ткань, чем у гауссова луча. Световая микроскопия на основе пучка Бесселя была впервые продемонстрирована в 2010 году, но с тех пор последовало много изменений. В 2018 году было показано, что использование компенсации затухания может быть применено к световой микроскопии на основе пучка Бесселя и может обеспечить получение изображений на больших глубинах в биологических образцах.
Подводные системы звуковидения и акустическая голография
Большое внимание уделяется в настоящее время акустической голографии. Акустические системы подводного видения имеют ряд преимуществ перед системами прямого оптического видения и гидролокационными системами обычного типа при наблюдениях в водной среде. Оптическое видение ограничивается сравнительно небольшими дальностями, особенно в мутной воде, а гидролокационные системы не обеспечивают детальной информации о цели. Акустическая голография позволяет создать систему видения, на которую мало влияет турбулентность и мутность воды и которая может воспроизводить изображения подводных объектов в сравнительно большом угле поля зрения при большей дальности видения по сравнению с оптическими системами.
Акустическая жидкость
Пучки Бесселя являются хорошим кандидатом для выборочного захвата из-за концентрических окружностей максимального и минимального давления в поперечных плоскостях.
Акустические линзы
устройство для фокусировки звука путём изменения длины пути, проходимого акустич. волной, и её преломления (рефракции) на граничных поверхностях. Свойства Л. определяются свойствами материала линзы и окружающей её среды и формой преломляющих поверхностей линзы. Показатель преломления Л. n=с1/с2, где с2 и с1 — скорости волн в материале линзы и в окружающей среде соответственно. При n>1 (с2<с1) собирающая линза имеет хотя бы одну выпуклую преломляющую поверхность и наз. замедляющей. При n<1 (c2>c1) собирающая Л. имеет хотя бы одну вогнутую преломляющую поверхность в наз. ускоряющей. Материал для Л. должен обладать миним. затуханием и волновым сопротивлением, близким к волновому сопротивлению окружающей среды. Л. изготавливают из тв. материалов, жидкостей и газов. В последних двух случаях используют оболочку, обеспечивающую макс. прохождение энергии и незначит. отклонение лучей при преломлении. Ускоряющие Л. обладают меньшими сферич. аберрациями, чем замедляющие.

