Файл: Образования российской федерации.docx

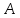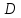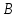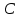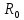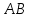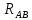и , на стороне приёмника измеряется разность потенциалов между узлами и , сопротивление приёмника равно , сопротивление провода равно , сопротивление провода 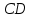равно , внутреннее сопротивление источника ЭДС пренебрежимо мало. Используя формулу закона Ома, получаем систему уравнений:




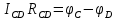
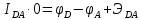
Согласно первому правилу Кирхгофа, силы токов в левых частях уравнений равны одному и тому же значению ; электрический ток проходит через источник ЭДС от отрицательного полюса к положительному, следовательно, значение электродвижущей силы источника ЭДС 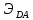равно положительному числу E. Таким образом,





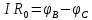
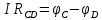
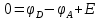
Сложим все четыре уравнения:


где – сопротивление проводов: ,

---

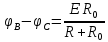
Периодические функции
Говорят, что величина является функцией величины , когда каждому допустимому значению величины (независимой переменной или аргумента функции) соответствует однозначно определённое значение величины . Чтобы показать функциональную зависимость величины от величины пишут

Предполагается, что значения величины принадлежат множеству, которое называется областью определения функции , а значения величины принадлежат множеству, которое называется областью значений функции . Символ обозначает отношение между элементами области определения функции и элементами области её определения, которое ставит в соответствие каждому значению аргумента значение функции. Аргументами и значениями числовых (скалярных) функций являются вещественные числа. В технике чаще всего встречается функциональная зависимость между величиной, характеризующей состояние системы, и временем: каждому моменту времени функционирования технической системы ставится в соответствие одно определённое значение величины, характеризующее состояние системы в данный момент времени.
Функция 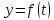, определённая на числовой прямой, называется периодической, если существует такое отличное от нуля число , что для всех значений аргумента справедливо равенство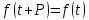

---

В этом случае


и вообще

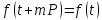
где – произвольное целое (положительное или отрицательное) число. Периодом функции 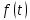называется наименьшее положительное число 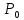, для которого равенство

для любого значения аргумента 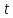. Если 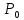– период функции 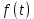, P – вещественное число, то следующие утверждения равносильны (оба истинные или оба ложные):

для любого значения аргумента
;
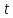
существует такое целое число , что
Синус и косинус
В практических задачах угол обычно определяется как скалярная величина, характеризующая поворот направленного отрезка в координатной плоскости вокруг его начала. Если направленный отрезок поворачивается против движения часовой стрелки (с точки зрения наблюдателя), то длина дуги, которую описывает конец направленного отрезка, считается положительным, если же отрезок поворачивается по часовой стрелке, то длина дуги считается отрицательным. Числовое значение угла равно отношению длины дуги, которую описывает конец направленного отрезка (учитывая знак), к длине направленного отрезка. Единица измерения угла называется радианом. Радиан равен углу, на который поворачивается направленный отрезок в координатной плоскости , вращаясь вокруг начала координат , в том случае, когда длина дуги окружности, которую описывает конец отрезка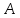

---

равен длине её радиуса . Один радиан составляет 57°,2958 или 57°17'44,8'', это число равно отношению 180° / π. Радиан - дополнительная единица Международной системы СИ.

Углом также называют геометрическую фигуру, образованную двумя ненулевыми направленными отрезками с общим началом.

Проекцией точки A на прямую d называется основание перпендикуляра, опущенного точки A на 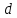. Проекция направленного отрезка AB на прямую d - это направленный отрезок A₀B₀, началом которого является проекция точки A на d, а концом - проекция на d точки B. Аналогично определяются проекции точки, направленного отрезка и прямой на плоскость.

Прямая, на которой выбрано направление, называется осью. Если направление проекции направленного отрезка 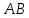на ось 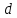совпадает с направлением оси, то её обычно отождествляют с длиной проекции – положительным вещественным числом ,

если направление проекции направленного отрезка 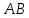на ось 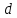противоположно направлению оси, то её отождествляют с отрицательным вещественным числом 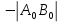(минус ),

если концы проекции направленного отрезка 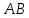на ось 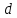совпадают, то её отождествляют с нулём,

Координатами направленного отрезка называются представления его проекций на три взаимно перпендикулярные оси координат, проходящие через одну точку (начало координат), в виде вещественных чисел. Два направленных отрезка имеют одинаковые длины и направлены в одну и ту же сторону в том и только в том случае, когда их координаты совпадают. Координатами точки служат координаты её радиуса-вектора. Выбор осей координат устанавливает взаимно однозначное соответствие между точками пространства и их координатами (слайд Координаты направленного отрезка, файл PP_Разработка Web-служб).

---

Косинусом называется функция, которая ставит в соответствие вещественному числу φ отношение абсциссы направленного отрезка OA (представления его проекции на ось Ox в виде вещественного числа), лежащего на плоскости Oxy и образующего с осью Ox угол, равный φ радиан, к его длине. Отношение ординаты этого отрезка (представления его проекции на ось Oy в виде вещественного числа) к его длине будет значением синуса вещественного числа φ, оси Ox и Oy взаимно перпендикулярны (слайд Синус и косинус, файл PP_ Разработка Web-служб). По теореме Пифагора
cos² φ + sin² φ = 1.
Это соотношение называется основным тригонометрическим тождеством. Косинус числа минус φ равен косинусу φ, синус числа минус φ равен числу, противоположному синусу φ:
cos ( - φ ) = cos φ,
sin ( - φ ) = - sin φ.
Координаты направленного отрезка OA являются функциями угла φ:
x = | OA | cos φ,
y = | OA | sin φ,
z = 0.
Проекция направленного отрезка на ось равна произведению модуля вектора на косинус угла между осью и вектором. Напомним, что проекции на ось направленных в одну сторону отрезков одинаковой длины равны между собой. Таким образом, можно говорить о проекции вектора на ось и о координатах вектора: эти понятия не зависят от выбора направленного отрезка, который представляет этот вектор.

Для определения тригонометрических функций синуса и косинуса можно использовать теорию дифференциальных уравнений. Косинус является единственным решением задачи Коши



Другими словами, функция 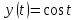– единственное решение дифференциального уравнения , значение которого в точке равно единице, а значение производной этой функции и точке равно нулю (напомним, что производная косинуса – минус синус, а производная синуса – это косинус: 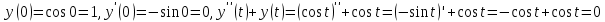). Такой подход позволяет получить представление косинуса в виде суммы степенного ряда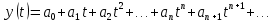

Действительно,

---