Файл: Образования российской федерации.docx

---

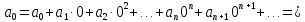
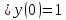
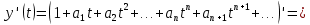
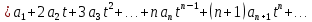
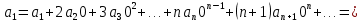
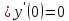
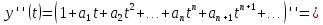
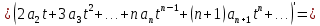
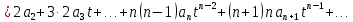
Подставляя в уравнение 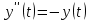вместо 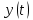и 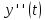соответствующие степенные ряды, получаем: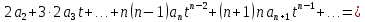



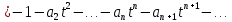
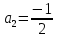
Аналогично вычисляются остальные коэффициенты степенного ряда:


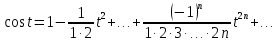
Это равенство означает, что для любого значения аргумента

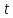
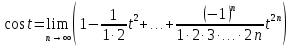
На практике степенной ряд заменяют многочленом:

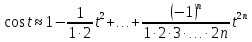
Можно показать, что в этом случае погрешность вычислений не превосходит

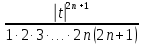
Точно так же разлагается в степенной ряд синус:


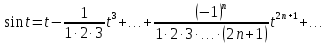
Разложение функции в степенной ряд позволяет вычислять её значения с любой заданной точностью.
Гармонические колебания
Гармоническим колебанием называется изменение значений физической величины 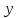с течением времени 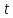, которое описывается функциональной зависимостью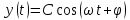

Период косинуса равен

---

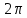, следовательно, период гармонического колебания равен 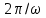. Действительно, если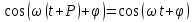

то



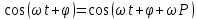
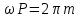
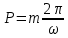
Параметр 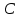называется амплитудой гармонического колебания (следует отличать амплитуду гармонического колебания 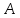от значения его амплитуды в момент времени 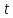, которое равно 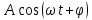), параметр 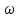называется круговой, угловой или циклической частотой, в системе СИ единицей измерения круговой частоты служит радиан в секунду (рад/с) или секунда в минус первой степени (с^-1), размерность угловой частоты – T^-1. Параметр 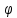называется начальной фазой гармонического колебания.

Функциональная зависимость

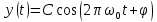
описывает периодическое колебание с частотой .

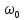Применяя формулу косинуса суммы, получим:



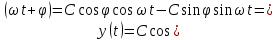
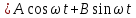
где 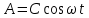и .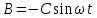

Обратно, пусть

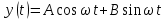
Положим

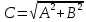
тогда

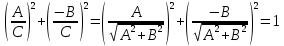
следовательно, существует такое вещественное число 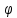, что,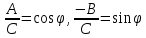

---

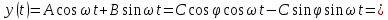
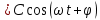
Следовательно, функция

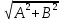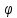описывает гармоническое колебание, амплитуда которого равна , круговая частота равна , а начальная фаза удовлетворяет условиям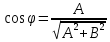


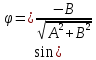
Примечание. Параметр – физическая величина, которая не изменяется в течение некоторого времени.
Тригонометрические многочлены
Сумма


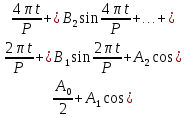
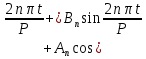
где – произвольное положительное число, называется тригонометрическим многочленом. Тригонометрический многочлен является периодической функцией: если прибавить к значению аргумента 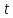число , значение тригонометрического многочлена не изменится. Обычно тригонометрический многочлен пишут со знаком сигма, который заменяет суммирование: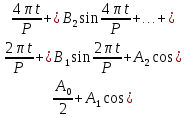



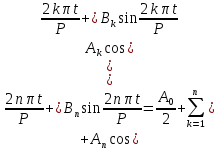
Справедливо следующее утверждение: если функция определенна на всей числовой прямой и для любого значения аргумента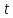

то значение интеграла квадрата разности

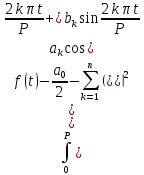
будет минимальным тогда и только тогда, когда





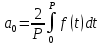
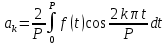
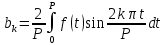
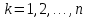. В этом случае коэффициенты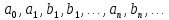

---

называются коэффициентами Фурье функции .
В математике квадратный корень из интеграла квадрата разности функций и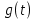

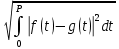
служит оценкой «расстояния» между функциями и 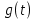на интервале 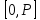. В этом смысле тригонометрический многочлен является наилучшим приближением функции в том и только в том случае, когда его коэффициенты равны соответствующим коэффициентам Фурье этой функции.

Если в точке 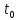периодическая функция непрерывна, то её ряд Фурье сходится в этой точке к значению функции: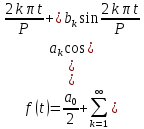

или



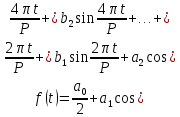
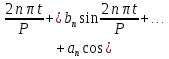
Это означает, что




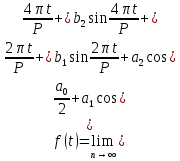
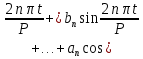
Пример 1. Комнатная электрическая розетка является электромеханическим устройством для электрического соединения и разъединения электрических цепей. В ней два контактных гнезда. Одно из них соединяется с заземлением, его электрический потенциал равен нулю. Другое контактное гнездо обычно называется фазой. Его электрический потенциал изменяется с течением времени. Функциональная зависимость электрического потенциала этого контактного гнезда от времени 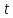описывается формулой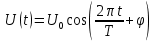

величина 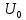называется амплитудой колебаний электрического потенциала,

---