Файл: О. А. Ивашова, О. В. Шереметьева Подготовка студентов к организации исследовательской деятельности младших школьников на уроках математики.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 28
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример поэтапной работы над исследовательским заданием
Материал взят из из статьи:
О.А. Ивашова, О.В. Шереметьева Подготовка студентов к организации исследовательской деятельности младших школьников на уроках математики/ Актуальные проблемы обучения в школах и вузах малых городов России: Материалы региональной научно-практической конференции 3-4 декабря 2002 года, г. Коряжма. - Архангельск: Поморский государственный университет имени М.В. Ломоносова, 2003. - с.35-39.
Этапы ИД | Выполняемые действия | |
Анализ информации | Актуализация знаний о развертке многогранника и, в частности, о развертке куба (плоская связанная фигура, составленная из шести равных квадратов, приложенных друг к другу сторонами так, что любые два квадрата имеют не более одной общей стороны); выяснение вопросов о том, как определить, является ли фигура из квадратов разверткой, какие развертки считать различными. | |
Проблема | Нахождение всех возможных разверток | |
Гипотеза | Можно найти все развертки, если последовательно рассмотреть случаи, когда в составленной из квадратов фигуре от одного до шести квадратов составляют полосу (прямоугольник со стороной, равной длине ребра куба). | |
План эксперимента | Строим полосу из шести (пяти, четырех, трех, двух, одного) квадратов.Достраиваем разными способами недостающие квадраты.Выбираем из получающихся при этом фигур такие, которые являются развертками куба (выполняем мысленное свертывание).Определяем равные развертки. | |
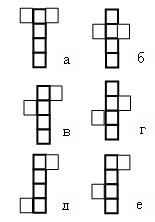
Эксперимент | Замечаем, что фигура, содержащая полосы из шести или пяти квадратов не может служить разверткой куба.Строим полосу из четырех квадратов и ищем различные варианты расположения оставшихся двух квадратов. Замечаем, что эти два квадрата всегда находятся по разные стороны от полосы и могут быть расположены на одном уровне относительно полосы (два варианта – рис. а и б) и на разных – на соседних (два варианта – рис. в и г) и не на соседних (два варианта – рис. д и е). Получили шесть разверток. | |
Строим полосу из трех квадратов и ищем различные варианты расположения оставшихся трех квадратов. Замечаем, что есть только один вариант развертки, когда оставшиеся три квадрата находятся по одну сторону от полосы (рис. ж). Для случая расположения одного квадрата по одну сторону от полосы, а двух других – по другую, есть три варианта разверток (рис. з, и и к). Получили четыре развертки. | 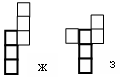 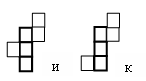 | |
Строим полосу из двух квадратов и выясняем, что существует только один вариант такой развертки, отличный от построенных ранее (рис. л). | 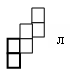 | |
Проверка | Для проверки того, что все найденные фигуры являются развертками куба, целесообразно провести практическую работу в группах: изготовить развертки в соответствии с найденными решениями и сложить из них модели кубов. | |
Доработка | Если в ходе работы среди найденных фигур обнаруживаются фигуры, которые не являются развертками куба (из них нельзя получить модель куба), то корректируют найденное в эксперименте решение.Если количество решений, найденных в одной группе, оказывается меньшим, чем в другой, первая группа, возвращаясь к результатам эксперимента, ищет недостающие варианты, корректируя тем самым результаты своей работы. В случае, когда ни одна из групп не нашла всех вариантов составления развертки, целесообразно еще раз обратиться к этапу эксперимента, т.е. анализу способа перебора. | |
Выводы |
| |