ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.05.2024
Просмотров: 10
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Номер | x | y | x^2 | y^2 | x*y | y(x) |
| 1 | 3,4 | 262 | 11,56 | 68644 | 890,8 | 261,8542587 |
| 2 | 1,8 | 178 | 3,24 | 31684 | 320,4 | 186,8660589 |
| 3 | 4,6 | 313 | 21,16 | 97969 | 1439,8 | 318,0954085 |
| 4 | 2,3 | 231 | 5,29 | 53361 | 531,3 | 210,2998714 |
| 5 | 3,1 | 275 | 9,61 | 75625 | 852,5 | 247,7939713 |
| 6 | 5,5 | 360 | 30,25 | 129600 | 1980 | 360,2762709 |
| 7 | 0,7 | 141 | 0,49 | 19881 | 98,7 | 135,3116716 |
| 8 | 3 | 223 | 9 | 49729 | 669 | 243,1072088 |
| 9 | 2,6 | 196 | 6,76 | 38416 | 509,6 | 224,3601588 |
| 10 | 4,3 | 313 | 18,49 | 97969 | 1345,9 | 304,0351211 |
| Сумма | 31,3 | 2492 | 115,85 | 662878 | 8638 | 2492 |
| Среднее | 3,13 | 249,2 | 11,585 | 66287,8 | 863,8 | 249,2 |
Система нормальных уравнений.
an + b∑x = ∑y
a∑x + b∑x2 = ∑yx
10a + 31.3·b = 2492
31.3·a + 115.85·b = 8638
Домножим уравнение (1) системы на (-3.13), получим систему, которую решим методом алгебраического сложения.
-31.3a -97.969 b = -7799.96
31.3*a + 115.85*b = 8638
Получаем:
17.881*b = 838.04
Откуда b = 46.8676
Теперь найдем коэффициент «a» из уравнения (1):
10a + 31.3*b = 2492
10a + 31.3*46.8676 = 2492
10a = 1025.043
a = 102.5043
Получаем эмпирические коэффициенты регрессии: b = 46.8676, a = 102.5043
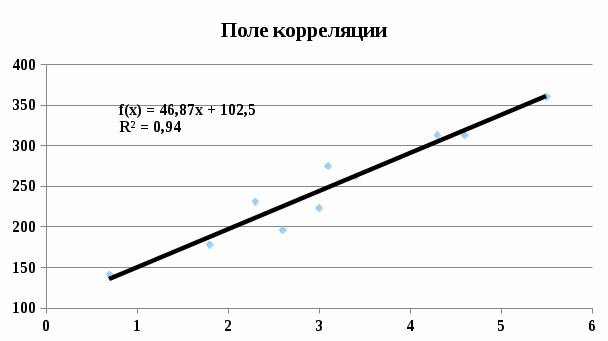
Уравнение регрессии:
y = 46.8676x + 102.5043
Выборочные средние.
Выборочные дисперсии:
Коэффициент линейной парной корреляции:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая
Связь между признаком Y и фактором X весьма высокая и прямая.
H0: rxy = 0, нет линейной взаимосвязи между переменными;
H1: rxy ≠ 0, есть линейная взаимосвязь между переменными.
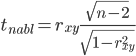
tкрит — нулевую гипотезу отвергают.
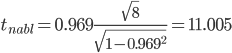
tкрит(n-m-1;α/2) = tкрит(8;0.025) = 2.752
Поскольку |tнабл| > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.