ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 27
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Непосредственное интегрирование
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.
[править] Подведение под знак дифференциала
Данный метод эквивалентен методу замены переменной (см. далее):
[править] Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл
Сделаем подстановку где — функция, имеющая непрерывную производную.Тогда
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
[править] Интегрирование выражений вида 
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.
[править] Примеры
Вычислить:
Пусть тогда и
[править] Интегрирование по частям
Основная статья: Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
В частности, с помощью n-кратного применения этой формулы находится интеграл
где Pn + 1(x) — многочлен (n + 1)-ой степени.
[править] Интегрирование рациональных дробей
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую правильную рациональную дробь , знаменатель которой разложен на множители
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
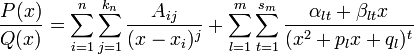
где Aij,αlt,βlt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
[править] Примеры
Вычислить:
Разложим подынтегральное выражение на простейшие дроби:
Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:
α(x + 3) + β(x − 3) = 2x + 3
(α + β)x + 3α − 3β = 2x + 3
Следовательно
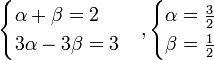
Тогда
Теперь легко вычислить исходный интеграл
| Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул: У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:  где  Затем применяются следующие формулы: Интеграл  может быть вычислен за k шагов с помощью формулы редукции |
| Пример 1 |
| |
| Вычислить интеграл  . Решение. Разложим подынтегральное выражение на простейшие дроби:  Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями: 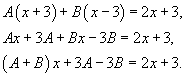 Следовательно, 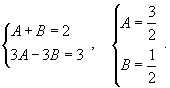 Тогда  Теперь легко вычислить исходный интеграл  |
| Пример 2 |
| |
| Вычислить интеграл 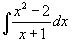 . Решение. Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель.  Получаем  |
| Пример 3 |
| |
| Вычислить интеграл  . Решение.  |
| Пример 4 |
| |
| Вычислить интеграл  . Решение. Разложим подынтегральное выражение на сумму простейших дробей, используя метод неопределенных коэффициентов:  Определим ы: 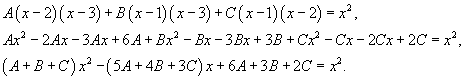 Следовательно, 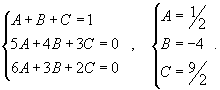 Получаем  Интеграл, соответственно, равен  |
| Пример 5 |
| |
| Найти интеграл  . Решение. Разложим подынтегральное выражение на сумму двух дробей.  Найдем неизвестные коэффициенты.  Отсюда получаем  Подынтегральное выражение представляется в виде 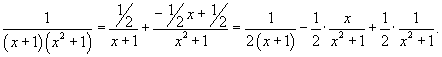 Исходный интеграл равен  |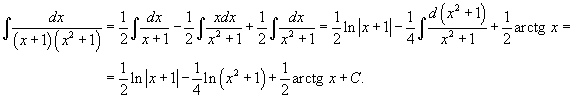
| Пример 6 |
| |
| Найти интеграл  . Решение. Разложим знаменатель в подынтегральном выражении на множители:  Далее представим подынтегральное выражение в виде суммы простейших дробей  Определим коэффициенты: 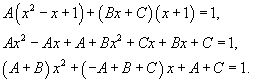 Следовательно, 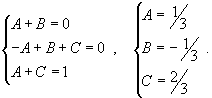 Отсюда находим  Теперь вычислим исходный интеграл  |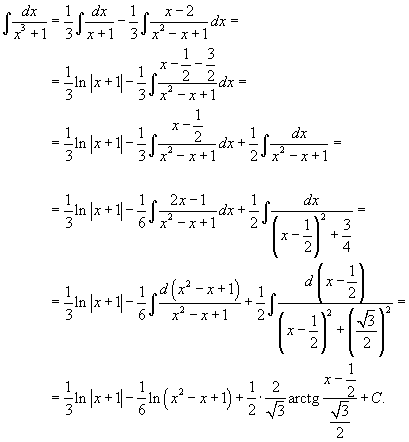
| Пример 7 |
| |
| Вычислить интеграл  . Решение. Перепишем знаменатель рациональной дроби в следующем виде:  Поскольку полученные множители являются несократимыми квадратичными функциями, то подынтегральное выражение представляется в виде 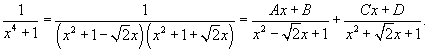 Определим неизвестные коэффициенты. 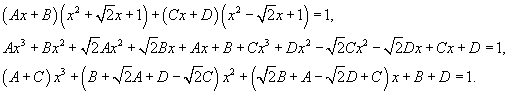 Получаем  Следовательно, 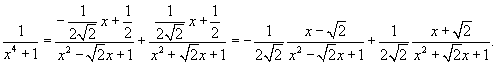 Интегрируем каждое слагаемое и находим ответ.  |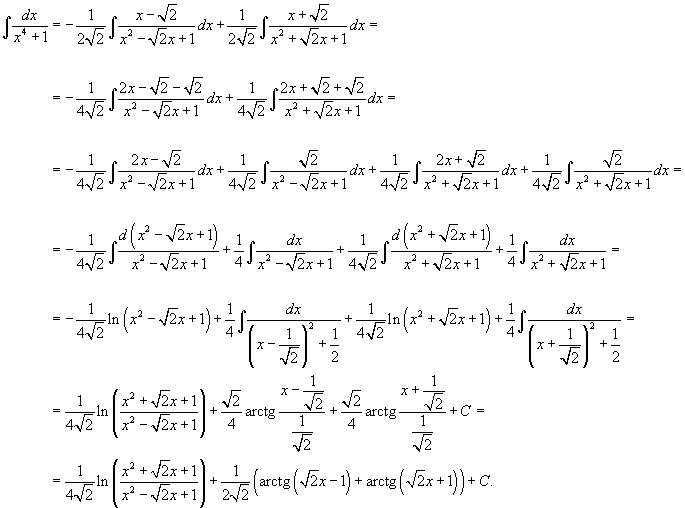
| Пример 8 |
| |
| Вычислить интеграл  . Решение. Разложим знаменатель на множители:  Запишем подынтегральную дробь в виде суммы простейших дробей.  Сгруппируем члены с одинаковыми степенями чтобы определить неизвестные коэффициенты из системы линейных уравнений. 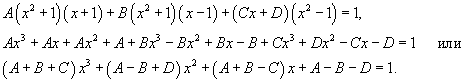 Следовательно, 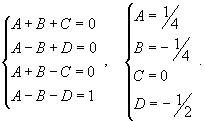 Таким образом, подынтегральное выражение представляется в виде  Окончательно находим  |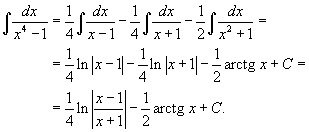
| Пример 9 |
| |
| Вычислить интеграл  . Решение. Разложим подынтегральное выражение на сумму простейших дробей, учитывая что знаменатель имеет кратный корень 3-го порядка:  Определим неизвестные коэффициенты. 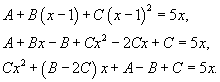 Получаем систему уравнений 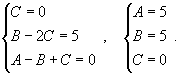 Следовательно,  Исходный интеграл равен  |
| Пример 10 |
| Вычислить интеграл 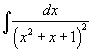 . Решение. Поскольку  - несократимый квадратный трехчлен, выделим в знаменателе полный квадрат:  Найдем полученный интеграл с помощью формулы редукции  Получаем ответ:  |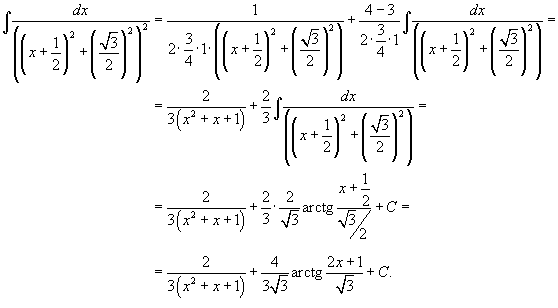
Пример.
Т.к. ( , то
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
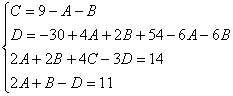
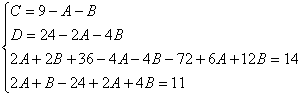
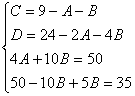
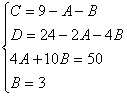
Итого:
Пример.
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
6x5 – 8x4 – 25x3 + 20x2 – 76x – 7 3x3 – 4x2 – 17x + 6
6x5 – 8x4 – 34x3 + 12x2 2x2 + 3
9x3 + 8x2 – 76x - 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
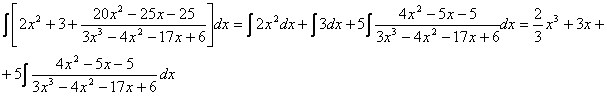
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
3x3 – 4x2 – 17x + 6 x - 3
3x3 – 9x2 3x2 + 5x - 2
5x2 – 17x
5x2 – 15x
- 2x + 6
-2x + 6
0
Таким образом 3x3 – 4x2 – 17x + 6 = (x – 3)(3x2 + 5x – 2) = (x – 3)(x + 2 )(3x – 1). Тогда:
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
Окончательно получаем:
= 
Пример.
Найдем неопределенные коэффициенты:
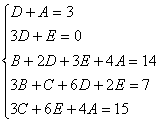
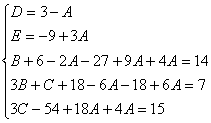
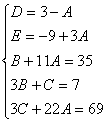
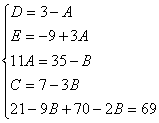
Тогда значение заданного интеграла:
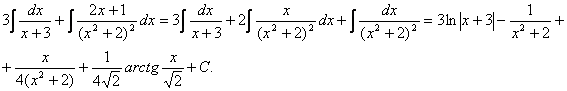
Пример 1
Найти неопределенный интеграл.
Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно