Томский межвузовский центр дистанционного образования

Томский государственный университет систем управления и радиоэлектроники (ТУСУР)

Кафедра компьютерных систем в управлении и проектировании (КСУП)

Контрольная работа № 2

по дисциплине «Математическая логика и теория алгоритмов»

(Учебное методическое пособие «Математическая логика и теория алгоритмов» В. М. Зюзьков, Томск - 2004)

Тема: ВТОРОЕ контрольное задание

Вариант 6

Вариант 6	1. Для бинарного отношения xy  «x + y делится нацело на 3», определенного на множестве Z целых чисел, выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает.
	2. Построить композицию следующих отношений («Быть A» означает «x является A для y».): быть родителем, быть сестрой (возможны две композиции, в зависимости от порядка отношений).
	3. Пусть  и  – бинарные отношения на некотором множестве. Докажите, что ()–1 = –1  –1.
	4. Найдите композиции  и , где  = ={<x,y>RR|x+y=0},  = {<x,y>RR|xy>0}, R – множество вещественных чисел.
	5. Доказать тождество для любой функции f и произвольных множеств A и B: f(A)\f(B) f(A\B).
	6. Является ли отношением эквивалентности отношение: иметь одну и ту же мать.
	7. Докажите, что M ={{1},{2},{3}} – разбиение множества A={1,2,3}. Перечислите все элементы отношения эквивалентности, соответствующего разбиению M.
	8. Используя математическую индукцию, докажите, что для n  2.
	9. Пусть X = {1, 2, 3, 4, 5, 6} и f – инъективная функция из X в множество–степень P(X), определенная следующим образом: f(1) = {2,3,4}, f(2) = {1,4,2}, f(3) = {2,4}, f(4) = , f(5) = {1,2,3,4,6}, f(6) = {1,3,2}. Опишите множество W, отсутствие отображения на которое гарантирует нам теорема 3.16 учебного пособия.
	10. Расположите следующие 4 функции в порядке увеличения скорости роста (каждая функция есть O(следующая)), не исключено, что некоторые функции имеют одинаковую скорость: f1(n) = , f2(n) = , f3(n) = 2n, f4(n) = n2.

---

1. Для бинарного отношения xy  «x + y делится нацело на 3», определенного на множестве Z целых чисел, выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает.

Решение.

Отношение  на множестве х называется рефлексивным, если для любого элемента хХ выполняется хх .

«х+х делится на цело на 3» выполнено не для всех хZ (например (1+4)/3 – в ответе получится дробное число)  нерефлексивно.

Отношение  на множестве х нозывают симметричным, если для любых х, уХ из ху следует ух.

Отношение  симметрично, потому что, если «х+у делится нацело на 3», то и «у+х делится нацело на 3»

Отношение  на множестве х называется транзитивным, если для любых х, у, zХ из ху и ух следует хz.

«х+у делится нацело на 3» и «у+z делится нацело на 3», но «х+z делится нацело на 3» выполняется не для всех z. Отношение нетранзитивное.

Отношение  на множестве х называется антисимметричным, если для любых х, уХ из ху и ух следует х=у.

«х+у делится на 3» и «у+х делится на 3», но не для всех х,у Z следует, что х=у, поэтому отношение неантисимметричное.

Ответ: нерефлективное, симметричное, нетранзитивное, неантисимметричное.
2. Построить композицию следующих отношений («Быть A» означает «x является A для y».): быть родителем, быть сестрой (возможны две композиции, в зависимости от порядка отношений).

Решение.

Композицией отношений XY и YZ называется отношение XZ, такое, что  = {<x,z> | xX & zZ & y(yY & <x,y> & <y,z>)}.

Имеем

<х,у> «х – родитель у»,

<х,у> «х – сестра у».

Поэтому ={<х,у> | существует z такой, что <х,z> и }={<х,у> | существует z такой, что х – родитель z и z – сестра у}={<х,у> | х – родитель сестры у}={<х,у> | х – отчим у, если сестра сводная}
={<х,у> | существует z такой, что <х,z> и }={<х,у> | существует z такой, что х – сестра z и z – родитель у}={<х,у> | х – сестра родителя у}={<х,у> | х – тетя у}
3. Пусть  и  – бинарные отношения на некотором множестве. Докажите, что

()^–1 = ^–1  ^–1.

Решение.

Пусть <х,у>()^–1 <х,у><х,у> и <х,у><х,у>^–1 и <х,у>^–1  ^–1  ^–1.
4. Найдите композиции  и , где ={<x,y>RR|x+y=0}, = {<x,y>RR|xy>0}, R – множество вещественных чисел.

Решение.

={<х,у> | существует z такой, что <х,z> и }={<х,у> | существует z такой, что х+z=0 и zу>0}.

(х+z=0 в том случае, если х и z равны по модулю, но противоположны по знаку, либо х=z=0.

zу>0 в том случае, если z и у оба положительны, либо z и у оба отрицательны, но не один из них не равен нулю.)

Если у0, то такое z найдется. Поэтому = R(R\{0}).

={<х,у> | существует z такой, что <х,z> и }={<х,у> | существует z такой, что хz>0 и z+у=0}.

(xz>0 в том случае, если x и z оба положительны, либо x и z оба отрицательны, но не один из них не равен нулю.

z+у=0 в том случае, если z и у равны по модулю, но противоположны по знаку, либо х=z=0.)

Если х0, то такое z найдется. Поэтому = (R\{0})R.
5. Доказать тождество для любой функции f и произвольных множеств A и B:

f(A)\f(B) f(A\B).

Решение.

хf(A)\f(B)f(х)А и f(х)Вf(х)f(A\B).
6. Является ли отношением эквивалентности отношение: иметь одну и ту же мать.

Решение.

Рефлексивное, симметричное и транзитивное отношение  на множестве х называется отношением эквивалентности на множестве х.

<х,у> «х имеет одну и ту же мать с у»

Рефлексивность: хх («х имеет одну и ту же мать с х»). Отношение рефлексивно.

Симметричность: ху «х имеет одну и ту же мать с у» ух. Отношение симметрично.

Транзитивность: ху и уz  «х имеет одну и ту же мать с у» и «у имеет одну и ту же мать с z»  «х имеет одну и ту же мать с z» хz. Отношение транзитивно.

Поэтому отношение является отношением эквивалентности.
7. Докажите, что M ={{1},{2},{3}} – разбиение множества A={1,2,3}. Перечислите все элементы отношения эквивалентности, соответствующего разбиению M.

Решение.

Каждый элемент из А принадлежит какому-то элементу из М, причем только одному, следовательно, М – разбиение.

={<1,1>, <2,2>,<3,3>}.
8. Используя математическую индукцию, докажите, что

для n  2.

Решение.

Доказательство.

Пусть S_n есть утверждение для n  2.

Базис индукции. Докажем S_1.

При n=2 посчитаем, чему равна левая часть равенства: .

Справа получаем

.

Так что S₁ истинно.

Индуктивный переход.

Предполагаем, что для любого k2 утверждение S_к истинно.

Это означает, что .

Теперь необходимо доказать, что S_к+1 истинно. Другими словами требуется доказать, что .

Используя предположение (1) и сравнивая это равенство с (2), замечаем, что, умножив обе части равенства (1) на , получим равенство (2).


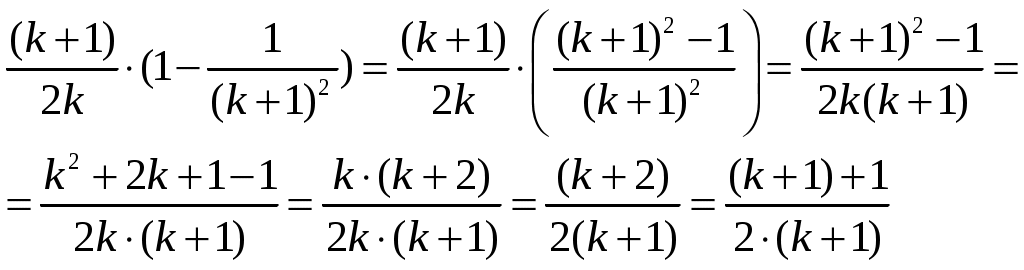
9. Пусть X = {1, 2, 3, 4, 5, 6} и f – инъективная функция из X в множество–степень P(X), определенная следующим образом:

f(1) = {2,3,4},

f(2) = {1,4,2},

f(3) = {2,4},

f(4) = ,

f(5) = {1,2,3,4,6},

f(6) = {1,3,2}.

Опишите множество W, отсутствие отображения на которое гарантирует нам теорема 3.16 учебного пособия.

Решение.

Теорема 3.16. Никакое множество Х не равномощно множеств Р(х) всех своих подмножеств.

W={х | хХ и хf(х)}.

Тогда W={1,3,4,5,6} – множество из доказательства теоремы, и в него не отображается никакой элемент.
10. Расположите следующие 4 функции в порядке увеличения скорости роста (каждая функция есть O(следующая)), не исключено, что некоторые функции имеют одинаковую скорость:

f₁(n) = , f₂(n) = , f₃(n) = 2ⁿ, f₄(n) = n².

Решение.

Для оценки производительности алгоритмов можно использовать разные подходы. Самый бесхитростный - просто запустить каждый алгоритм на нескольких задачах и сравнить время исполнения. Другой способ - математически оценить время исполнения подсчетом операций.

Математическое толкование символа O().
Определение
O(g) - множество функций f, для которых существуют такие константы C и N, что |f(x)| <= C|g(x)| для всех x>N.
Запись f = O(g) дословно обозначает, что f принадлежит множеству O(g). При этом обратное выражение O(g) = f не имеет смысла.

Итак, O() - асимптотическая оценка алгоритма на худших входных данных.
По условию задачи каждая функция есть О большее от следующая:
f₁(n) = = О ( )

f₂(n) = = О (2ⁿ)

f₃(n) = 2ⁿ= О (n²)

f₄(n) = n² = О ( )

Предположу, что:

О ( ) и О (2ⁿ) имеют равные скорости роста сложности. Самым сложным будет О( ), самым быстрым - О (n²).

Тогда правильный порядок для этих функций следующий:

f₃(n) = 2ⁿ= О (n²)

f₂(n) = = О (2ⁿ) и f₁(n) = = О ( )

f₄(n) = n² = О ( )

---

Смотрите также файлы

• Программа среднего профессионального образования Специальное дошкольное образование Дисциплина Физическая культура Практическое задание 2.docx

• Дисциплина История экономических учений Лектор кандидат исторических наук, доцент кафедры Эиасу юти тпу соловенко Игорь Сергеевич.ppt

• Государственное образовательное учреждение высшего профессионального образования луганской народной республики.pdf

• Кейс 2 1.docx

• Н. Ну, конечно же, салат оливье.docx