Файл: Практическая работа 3 Расчет тарифов страхования (методика 1).docx

Подставив полученные данные в систему уравнений, получим:

a₀ x 5 + a₁ x 15 = 1,48,

a₀ x 15 + a₁ x 55 = 4,96

Решив систему уравнений, получаем следующие значения:

a₀ = 0,14,

a₁ = 0,052,

на основании которых можно определить выравненную убыточность по годам, подставляя необходимые данные в уравнение.

Таким образом, ожидаемая убыточность на 1993 год с учетом тренда исходных данных составит:

y₆ = a₀ + a₁ x 6,

y₆ = 0,14 + 0,052 x 6 = 0,452 руб. со 100 руб. страховой суммы, т.е. это и является основной частью нетто - ставки;

в) для определения рисковой надбавки необходимо по следующей формуле рассчитать среднее квадратическое отклонение фактических значений убыточности от выравненных значений:

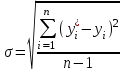(7.9.4)

Используемые для определения рисковой надбавки показатели приведены в таблице 7.9.2:

Таблица 7.9.2

Рисковые надбавки

Годы	i	Фактическая убыточность (yi)	Выравненная убыточность (y*i)	Отклонения выравненной убыточности от фактической (y*i - yi)	Квадраты отклонений (y*i - yi)2
1988	1	0,18	0,192	+0,012	0,000144
1989	2	0,26	0,244	-0,016	0,000256
1990	3	0,29	0,296	+0,006	0,000036
1991	4	0,36	0,348	-0,012	0,000144
1992	5	0,39	0,400	+0,010	0,000100
	15	1,48

Подставив рассчитанные показатели в формулу (7.9.4), получим:



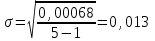
г) нетто - ставка рассчитывается следующим образом:

---

T_n = y₆ + β (γ; n) x σ,

где β (γ; n) - коэффициент, используемый для исчисления размера рисковой надбавки. Величина β (γ; n) зависит от заданной гарантии безопасности γ (той вероятности, с которой собранных взносов хватит на выплаты страховых возмещений) и n - числа анализируемых лет и может быть взята из таблицы 7.9.3.

Таблица 7.9.3

Коэффициент, используемый для исчисления размера рисковой надбавки

γ n	0,8	0,9	0,95	0,975	0,99
3	2,972	6,649	13,640	27,448	68,740
4	1,592	2,829	4,380	6,455	10,448
5	1,184	1,984	2,850	3,854	5,500
6	1,980	1,596	2,219	2,889	3,900

Допустим, страховая компания считает необходимым с уровнем вероятности γ = 0,9 быть уверена в том, что собранной суммы взносов будет достаточно для выплаты страховых возмещений. Тогда из таблицы 4 при γ = 0,9 для n = 5, бета = 1,984.

Нетто - ставка со 100 руб. страховой суммы

T_n = 0,452 + 1,984 x 0,013 = 0,48 (руб.).

Брутто - ставка (T_б) определяется по следующей формуле:
(7.9.5)
где T_n - нетто - ставка,

f(%) - доля нагрузки в общей тарифной ставке.

При условии, что нагрузка определена страховой организацией в размере 30% от брутто - ставки, рассчитывается брутто - ставка:



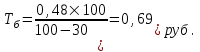
Брутто - ставка со 100 руб. страховой суммы равна 0,69 руб.

Задание для самостоятельной работы

На основе данных варианта (таблица 7.9.4) рассчитать брутто-ставку страхового тарифа по массовым рисковым видам страхования.

Таблица 7.9.4

Варианты для самостоятельной работы

Вариант	Фактическая убыточность страховой суммы по годам						β		Рисковая нагрузка
	1 год	2 год	3 год	4 год	5 год	6 год
1	0,21	0,18	0,25	0,15	0,16	0,22		0,95		40
2	0,18	0,19	0,18	0,14	0,15	0,23		0,8		35
3	0,25	0,2	0,16	0,21	0,14	0,19		0,99		30
4	0,21	0,23	0,18	0,22	0,21	0,18		0,95		25
5	0,18	0,17	0,19	0,23	0,22	0,17		0,9		30
6	0,17	0,16	0,23	0,19	0,23	0,16		0,95		35
7	0,28	0,15	0,21	0,15	0,19	0,22		0,99		40
8	0,27	0,22	0,19	0,22	0,18	0,21		0,8		35
9	0,26	0,23	0,16	0,23	0,17	0,2		0,8		30
10	0,25	0,24	0,15	0,24	0,16	0,19		0,99		25

---

Решение:

1) На основании ряда исходных данных рассчитываем прогнозируемый уровень убыточности страховой суммы, для чего используем модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения:



где y_i^* – выравненный показатель убыточности страховой суммы,

a₀, a₁ – параметры линейного тренда,

i – порядковый номер соответствующего года.

Параметры линейного тренда можно определить методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными:



,

где n – число анализируемых лет.

2) Запишем исходные данные в удобном для расчетов виде, а также найдем коэффициенты данной системы уравнений. Результаты представлены в таблице 7.9.5.

Таблица 7.9.5

Расчет коэффициентов

Годы (i)	Фактическая убыточность (yi)	Расчетные показатели
		yi*i	i2
1	0,26	0,26	1
2	0,23	0,46	4
3	0,16	0,48	9
4	0,23	0,92	16
5	0,17	0,85	25
6	0,2	1,2	36
21	1,25	4,17	91

Подставив полученные данные в систему уравнений, получим:

a₀*6 + a₁*21 = 1,25,

a₀*21 + a₁*91 = 4,17.

Решив систему уравнений, получаем следующие значения:

a₀ = 0,25,

a₁ = - 0,0117,

на основании которых можно определить выравненную убыточность по годам, подставляя необходимые данные в линейное уравнение.

Таким образом, ожидаемая убыточность на 7 год с учетом тренда исходных данных составит:

---

y₇ = a₀ + a₁*7,

y₇ = 0,25 – 0,0117*7 = 0,1681 руб. со 100 руб. страховой суммы, т. е. это и является основной частью нетто-ставки.

3) Для определения рисковой надбавки рассчитаем среднее квадратическое отклонение фактических значений убыточности от выравненных значений:



Используемые для определения рисковой надбавки показатели приведены в таблице 7.9.6.

Таблица 7.9.6

Рисковые надбавки

Годы (i)	Фактическая убыточность (yi)	Выравненная убыточность (y’i)	Отклонения выравненной убыточности от фактической (y’i – yi)	Квадраты отклонений (y’i – yi)2
1	0,26	0,2383	-0,0217	0,00047
2	0,23	0,2266	-0,0034	0,0000115
3	0,16	0,2149	+0,0549	0,003014
4	0,23	0,2032	-0,0268	0,000718
5	0,17	0,1915	+0,0215	0,000462
6	0,2	0,1798	-0,0202	0,000408
21	1,25			0,0050835

Подставив рассчитанные показатели в формулу для рисковой надбавки, получим:

.

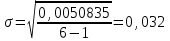4) Нетто-ставку рассчитываем следующим образом:

T_n = y₇ + β (γ; n) * σ,

где β (γ; n) – коэффициент, используемый для исчисления размера рисковой надбавки. В данном случае β (γ; n) = 0,8 (из исходных данных).

Нетто-ставка со 100 руб. страховой суммы составит:

T_n = 0,1681 + 0,8*0,032= 0,1937 (руб.).

Брутто-ставка (T_б) определяется по следующей формуле:
,

где T_n – нетто-ставка,

f (%) – доля нагрузки в общей тарифной ставке.

По условию нагрузка определена страховой организацией в размере 30% от брутто-ставки, тогда брутто-ставка составит:

---

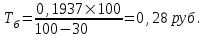
Таким образом, брутто-ставка со 100 руб. страховой суммы равна 0,28 руб.

---