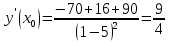
Тогда уравнение касательной



Уравнение нормали



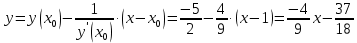
6. Найти пределы

1)

, так как степень числителя больше степени знаменателя

2)









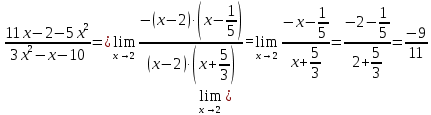
3)





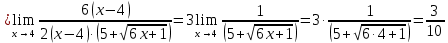
4)





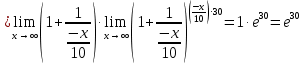
7. Провести полное исследование функции и построить график.



Область определения функции



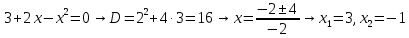
Таким образом, область определения функции



Исследуем поведение функции в окрестности точек разрыва









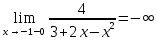
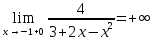
Таким образом, точки и — разрывы второго рода.

Функция не чётная, ни нечётная



Функция непериодическая.

Точки пересечения с осями координат

---

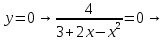
решений нет, график функции не пересекает ось .

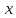Асимптоты функции

Точки и — разрывы второго рода, следовательно — вертикальные асимптоты.

Наклонные асимптоты:









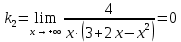
— горизонтальная асимптота.

Стационарные точки





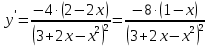
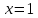— стационарная точка; .

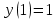Интервалы монотонности функции:

;

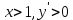
Функция убывает на , функция возрастает на .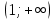









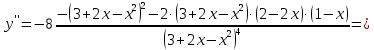
Точ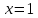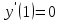ка : , точка 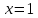— локальный минимум.

Точки перегиба

---

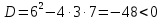
Точек перегиба нет.

Интервалы выпуклости функции







Функция выпукла вверх на .

Функция выпукла вниз на .

---

Смотрите также файлы

• Конспект викторины по изо весёлые художники.doc

• Практических заданий по дисциплине инновационный менеджмент.docx

• Специальные свойства строительных материалов.docx

• Искусство вокруг нас.ppt

• С нач ала Пе р вой ми ро вой вой ны он по лу чи л на з ван ие День Гер оев.pptx