Файл: Программа среднего профессионального образования 44. 02. 03. А педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Математика Практическое занятие 2.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 13
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая профессиональная образовательная организация "Национальный социально-педагогический колледж"
Программа среднего профессионального образования
44.02.03.А Педагогика дополнительного образования (в области социально-педагогической деятельности)
Дисциплина: Математика
Практическое занятие 2
Выполнил:
Обучающийся Матвеева Дарья Сергеевна
Преподаватель:
Сазонова Элеонора Борисовна
Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; закрепление навыков решения простейших статистических задач; закрепление навыков применять правила приближенных вычислений; закрепление навыков работы с основными свойствами геометрических фигур на плоскости и в пространстве.
Задание 1. (Максимальное количество баллов – 3 балла)
Таблица – «Виды моделирования при решении текстовых задач»
В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».
| Задача | Модель | Интерпретация модели |
| 1. 1. Было 7 кубиков, проиграно 4 кубика. Сколько кубиков осталось? | 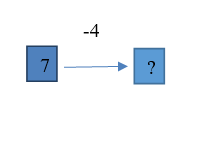 | Пример ответа: Известно: начальное состояние объекта; направленность отношения между начальным и конечным состоянием объекта; числовое значение величины отношения между состояниями объекта. Необходимо определитьчисловое значение величины конечного состояния объекта. |
| 2. Было 4 кубика, стало 7 кубиков. Что произошло? | 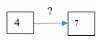 | Известно: начальное и конечное состояние объекта; направленность отношения между ними. Необходимо определить числовое значение величины отношения между состояниями объекта. |
| 3. Имеется 7 кубиков после того, как добавили 4 кубика. Сколько кубиков было до добавления? | 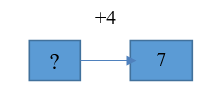  | Известно: значение величины конечного состояния объекта, направленность отношений между состояниями объекта и числовое значение величины отношений между состояниями объектов. Необходимо определитьзначение величины начального состояния объекта |
| 4.Было 7 кубиков, стало 4 кубика. Что произошло? |  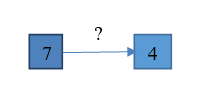 | Известно: значение величины начального и конечного состояния объекта, направленность отношений между состояниями объекта. Необходимо определитьчисловое значение величины отношений между состояниями объектов |
| 5.В первый раз принесли 7 кубиков, во второй раз – забрали 4 кубика. Что произошло в результате? | 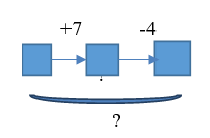 | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начального, промежуточного и конечного). Необходимо определитьчисловое значение величины отношений между начальным и конечным состояниями объектов |
| 6. В первый раз забрали 7 кубиков, во второй – принесли 4 кубика. Что произошло в результате? | 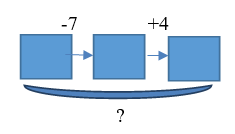 | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта. (начального, промежуточного и конечного). Необходимо определитьчисловое значение величины отношений между начальным и конечным состояниями объектов |
| 7.В первый раз забрали 4 кубика. После того, как кубики забрали второй раз, всего было отдано 7 кубиков. Что произошло во второй раз? | 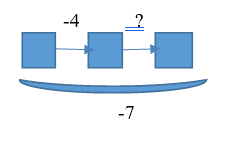 | Известно: направленность отношений между состояниями объекта; числовое значение величин отношений между состояниями объекта (начальным и промежуточным;начальным и конечным) Необходимо определитьчисловое значение величины отношений между промежуточным и конечным состояниями объектов |
| 8. В первый раз забрали 7 кубиков. После того, как во второй раз принесли кубики, оказалось, что всего было отдано 4 кубика. Что произошло во второй раз? | 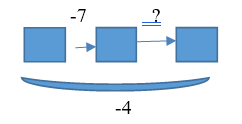  | Известно: направленность отношений между состояниями объекта; значение величин отношений между начальным и промежуточным, между промежуточным и конечным состоянием объекта. Необходимо определитьчисловое значение величины отношений между промежуточным и конечным состояниями объектов |
Задание 2. (Максимальное количество баллов – 3 балла)
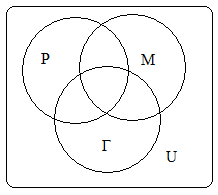
Используя диаграммы Эйлера-Венна решить задачу.
При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20% – сделали выбор в пользу занятий по гимнастике и музыке, а 40% родителей – пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые:
1) не желают водить детей в кружки;
2) выбрали не менее двух кружков.
Решение
В задаче речь идет о трех множествах:
Р – «родители, которые предпочли занятия по рисованию»
Г – «родители, которые предпочли занятия по гимнастике»
М – «родители, которые предпочли занятия по музыке (хоровое пение)»
U – универсальное множество (все родители, выбирающие кружки)
Известныследующиеданные:
|U|=100% |Р|=60%, |Г|=50%, |М|=50%, |Р
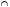 Г|=30%, |Г
Г|=30%, |Г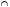 М|=20%,
М|=20%, |Р
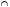 М|=40%, |Р
М|=40%, |Р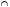 М
М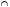 Г|= 10%
Г|= 10%Разметим диаграмму так, чтобы каждый родитель в ней участвовал только один раз. Т.е. определим мощности каждой из областей диаграммы.
1) Все три кружка: |Р
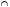 М
М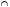 Г|= 10%
Г|= 10%2) Только рисование и гимнастика: |Р
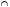 Г|-|Р
Г|-|Р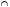 М
М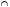 Г|=30%-10%=20%
Г|=30%-10%=20%3) Только рисование и музыка: |Р
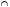 M|-|Р
M|-|Р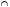
М
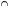 Г|=40%-10%=30%
Г|=40%-10%=30%4) Только гимнастика и музыка: |Г
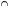 M|-|Р
M|-|Р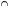 М
М Г|=20%-10%=10%
Г|=20%-10%=10%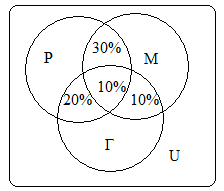
5) Только рисование: 60%-(30%+20%+10%)=0%
6) Только гимнастика: 50%-(20%+10%+10%)=10%
7) Только музыка: 50%-(30%+10%+10%)=0%
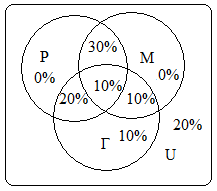
Значит |Р
 Г
Г М|=0%+10%+0%+30%+20%+10%+10%=80%
М|=0%+10%+0%+30%+20%+10%+10%=80%Получаем ответы:
Не желают водить детей в кружки: 100%-80%=20%
Выбрали не менее двух кружков: 30%+20%+10%+10%=70%
Ответ: 1)20%; 2) 70%
Задание 3. (максимальное количество баллов – 5 баллов)
При измерении получены данные:
| Номер измерения | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Данные | 20 | 20 | 5 | 10 | 10 | 15 | 20 | 5 | 5 | 20 |
Выполните задания с учетом исходных данных, подробно описывая ход решения.
a)Построить статистический ряд распределения частот.
b)Построить полигон распределения.
c)Вычислить выборочную среднюю, дисперсию, моду, медиану.
d)Построить выборочную функцию распределения.
Решение
Отсортируем данные в порядке неубывания, получим вариационный ряд
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 5 | 5 | 10 | 10 | 15 | 20 | 20 | 20 | 20 |
Строим статистический ряд распределения частот. Для каждого возможного значения выписываем частоту появления
| xi | 5 | 10 | 15 | 20 |
| ni | 3 | 2 | 1 | 4 |
Полигон распределения
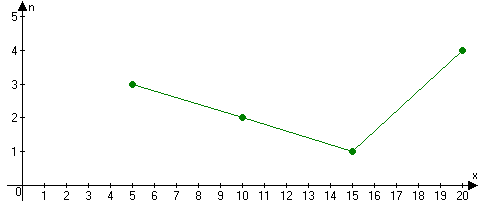
Выборочное среднее:
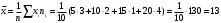
Дисперсия
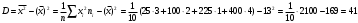
Мода
Наибольшая частота равна 4, ей соответствует значение 20, поэтому Мо=20
Медиана
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 5 | 5 | 10 | 10 | 15 | 20 | 20 | 20 | 20 |
Всего 10 вариант (четное число), поэтому, медиана:
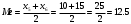
Строим статистический ряд распределения относительных частот
| xi | 5 | 10 | 15 | 20 |
| ni/10 | 0,3 | 0,2 | 0,1 | 0,4 |
Построимвыборочную функцию распределения.
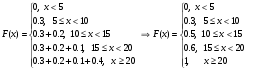
График:
